Расчет прочности сечений, нормальных к продольной оси балки
Поперечное сечение второстепенной балки является тавровым. При расчете на пролетные моменты полка тавра находится в сжатой зоне и участвует в работе, при расчете на опорные (отрицательные) моменты - в растянутой зоне и в работе на прочность не участвует (см. рис. 3.3).
В пролете сечения балки рассматриваем как тавровое, на опоре - прямоугольное.
Размеры сечения, принятые к расчету:
, 
, 
, 
.
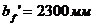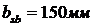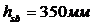Задаемся величиной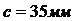 
в пролете и 
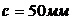на опоре, предполагая на ней расположение арматуры в два ряда, тогда:
, 
.
Предполагая, что нейтральная ось проходит по нижней грани полки, определяем область деформирования для прямоугольного сечения шириной 
и положение нейтральной оси при расчете тавровых сечений
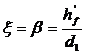. (3.3)
Рисунок 3.2 – Расчетная схема балки и огибающие эпюры изгибающих моментов и поперечных сил
;
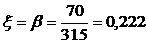что указывает на то, что сечение находится в области деформирования 1.б [2, таблица 3.3].
С помощью таблицы 3.3 находим величину изгибающего момента, воспринимаемого бетоном сечения, расположенным в пределах высоты полки
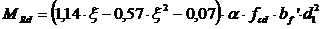, (3.4)
.
Поскольку выполняется условие 
, нейтральная ось расположена в пределах полки. Сечение в пролете второстепенной балки рассматривается как прямоугольное с шириной 
.
По [1, таблица 4.3] для бетона С20/25 находим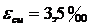 
, по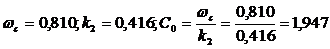 
.
Расчетные характеристики для арматуры класса S500: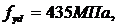 
, 
.
|
|
|
.
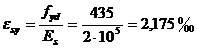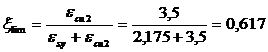
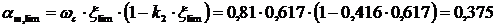В пролете 1 (нижняя арматура)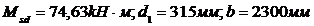 
.
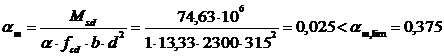, растянутая арматура достигла предельных деформаций.
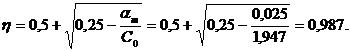
Требуемая площадь растянутой арматуры определяется по формуле
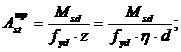(3.5)
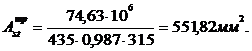
В пролете 2 (нижняя арматура) 
.
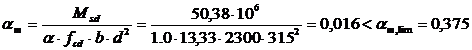, растянутая арматура достигла предельных деформаций.
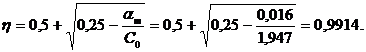
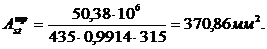
В опорных сечениях действуют отрицательные моменты, плита расположена в растянутой зоне, поэтому сечения балки рассматриваются как прямоугольные шириной b = 150 мм.
На опоре В (верхняя арматура)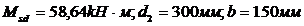 
.
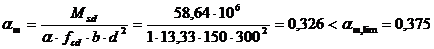, растянутая арматура достигла предельных деформаций.
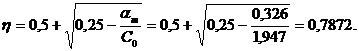
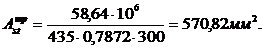
В пролете 2 (верхняя арматура) 
.
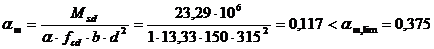, растянутая арматура достигла предельных деформаций.
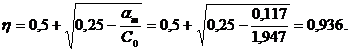
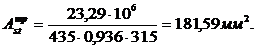
На опоре C (верхняя арматура)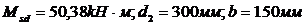 
.
, растянутая арматура достигла предельных деформаций.
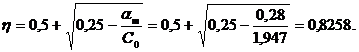
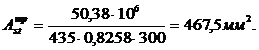
Результаты расчетов и подбор арматуры в расчетных сечениях сводим в таблицу 3.3.
Таблица 3.3 – Определение площади сечения рабочей арматуры второстепенной балки
| Положение сечения | Расположение арматуры |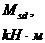 
| Расчетное сечение | 
| 
| 
| 
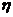
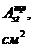
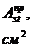
| Принятое армирование | ||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||
| 1 пролет | Нижняя | 74,63 | 
| 0,025 | 0,987 | 5,52 | 5,56 | 2Ø16и 1Ø14 | ||
| 1 пролет | Верхняя | - | 
| Монтажная конструктивная арматура
| 226 | 2Ø12 | ||||
| Опора В | Верхняя | 58,64 |
| 0,326 | 0,7872 | 5,71 | 5,75 | 3Ø14и 1Ø12 | ||
| 2 пролет | Нижняя | 50,38 | 
| 0,016 | 0,99 | 3,71 | 3,799 | 2Ø12и 1Ø14 | ||
Окончание таблицы 3.3
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 2 пролет | Верхняя | 23,29 |
| 0,117 | 0,936 | 1,82 | 2,26 | 2Ø12 |
| Опора С | Верхняя | 50,38 |
| 0,29 | 0,826 | 4,675 | 5,56 | 2Ø16и 1Ø14 |
Расчет прочности сечений, наклонных к продольной оси балки
Второстепенные балки армируют сварными каркасами и в отдельных случаях отдельными стержнями.
В учебных целях в курсовом проекте балку необходимо заармировать отдельными стержнями. В этом случае наклонные сечения армируют хомутами и отогнутыми стержнями. При этом хомуты назначают по конструктивным требованиям, а отогнутые стержни определяют расчетом.
Диаметр хомутов dω в вязанных каркасах изгибаемых элементов должен приниматься не менее 6 мм при высоте балки hsb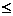 
800 мм и не менее 8 мм при hsb > 800 мм. Шаг хомутов S на приопорных участках (1/4 пролета) назначают в зависимости от высоты балки. При высоте балки hsb ≤ 450 мм не более hsb/2 и не более 150 мм; при hsb > 450 мм S ≤ hsb/3 и не более 500 мм. На остальной части пролета при hsb>300 мм поперечная арматура устанавливается с шагом S ≤ 3/4·hsb и не более 500 мм.
|
|
|
В нашем случае принимаем хомуты из стержней класса S240 диаметром 6 мм. Шаг хомутов в приопорных участках принимаем 150 мм, что меньше hsb/2 = 350/2 = 175 мм. На средних участках пролетов назначаем шаг хомутов равным 250 мм, что меньше 3/4 hsb = 3/4×350 = 262,5 мм и меньше 500 мм.
Расчет железобетонных изгибаемых элементов на действие поперечной силы для обеспечения прочности по наклонной полосе между наклонными трещинами должны проверятся по:
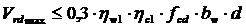(3.6)
где hw1 - коэффициент, учитывающий влияние хомутов, нормальных к продольной оси элемента.
но не более 1,3. (3.7)
Отношение модулей упругости арматуры и бетона:
; (3.8)
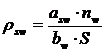, (3.9)
где asw=0,283 см2 –для одного стержня диаметром 6мм;
. (3.10)
.
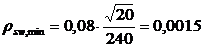Es = 20·104 МПа –для арматуры класса S240;
Ecm = 32·103 МПа для бетона класса С20/25 марка удобоукладываемости П1, П2.
|
|
|
.
.
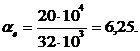
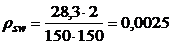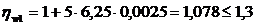, (3.11)
где β4-коэффициент, принимаемый для тяжелого бетона равным 0,01.
.
Уточняем значение рабочей высоты сечения d = 350 – 30 = 300 мм.
.
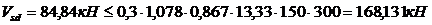Следовательно, прочность по наклонной полосе между наклонными трещинами обеспечена.
Вычисляем поперечную силу, которую могут воспринять совместно бетон и поперечная арматура по наклонной трещине по формуле
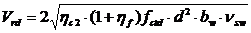, (3.12)
hс2 = 2 для тяжелого бетона.
hf - коэффициент, учитывающий влияние сжатых свесов полки.
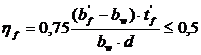, (3.13)
где (bf’ - bw) ≤ 3×tf’;
2300 – 150 = 2150 > 3·70 = 210 мм.
Принимаем в расчет 210 мм.
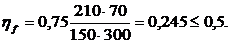
Находим линейное усилие которое могут воспринять хомуты
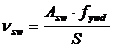, (3.14)
fywd - расчетное сопротивление поперечной арматуры (приняты поперечные стержни ⌀6 S240 с As = 28,3 мм2, шаг 150 мм) fywd = 174 МПа.
.
.
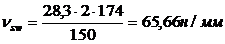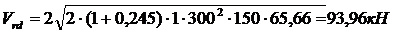Поперечная сила которую могут воспринять хомуты и бетон Vrd, = 93,96 кН > Vsd = 84,84 кН, следовательно прочность наклонного сечения обеспечена.
Дата добавления: 2018-02-15; просмотров: 1374; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!