Регулирование угловой скорости ДПТ
Регулирование угловой скорости ДПТ независимого и последовательного возбуждения введением добавочных сопротивлений в цепь якоря
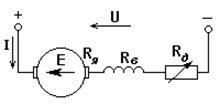
Схема подключения ДПТ НВ для этого способа регулирования приведена на рис. 13. На якорь и обмотку возбуждения двигателя подается номинальное напряжение: 
Рис. 13.Схема подключения ДПТ НВ при регулировании скорости введением добавочного сопротивления.
Электромеханическая и механическая характеристики двигателя описываются уравнениями (1.11), (1.12), в которых принято 
,
Рис. 14. Механическая характеристика ДПТ НВ при реостатном регулировании.
Очевидно, что первое слагаемое в этих уравнениях 
остается неизменным, а второй член – падение угловой скорости от нагрузки тем больше, чем больше добавочное сопротивление. Иными словами, с увеличением 
жесткость характеристик снижается (см. рис. 14):
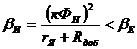(1.25)
Если, например, механизм имеет характеристику с моментом 
, не зависящим от скорости, то на естественной характеристике угловая скорость электропривода определяется т.1 (см. рис. 14), а при введении добавочных сопротивлений 
и 
снижается (т.2, т.3). Получаемые при введении добавочных сопротивлений характеристики называются искусственными – реостатными.
Рассматриваемый способ регулирования имеет ряд существенных недостатков. Во-первых, он не экономичен – часть энергии подводимой от преобразователя теряется в добавочном сопротивлении. Во-вторых, 
регулируется ступенчато, что не всегда удобно. В-третьих, при изменении момента статического сопротивления угловая скорость изменяется. Так, например, если момент сопротивления механизма уменьшится до 
, (см. рис. 14), то угловая скорость электропривода будет определиться т.т. 4, 5, 6.
|
|
|
В электроприводе с двигателем последовательного возбуждения при U=Uн (рис. 15 а) и известной естественной характеристике
(1.26)
можно использовать уравнение искусственных характеристик при реостатном регулировании
и получить соотношение для расчета wи для любого тока:
(1.26’)
а) б)
Рис. 15. Схема (а) и характеристики (б) при реостатном регулировании двигателя последовательного возбуждения
Механическая характеристика может быть построена по известной зависимости М(I). Примерный вид механических характеристик при реостатном регулировании показан на рис. 15 б.
|
|
|
Проведем оценки реостатного способа регулирования.
1. Регулирование однозонное - вниз от основной скорости, так как вводя Rд, мы увеличиваем 
, и все искусственные характеристики в 1 квадранте располагаются ниже естественной.
2. Диапазон реостатного регулирования невелик (2-2,5):1, при изменении Мс на 40-50%.
Стабильность скорости - низкая, жесткость характеристик падает с ростом R. Из (2.5) имеем:
,
где с = kФн (в дальнейшем, желая подчеркнуть неизменность потока возбуждения двигателя, мы будем часто пользоваться символом с).
Тогда 
. Это свойство реостатного регулирования часто существенно осложняет его использование: небольшое случайное изменение Мс на низких скоростях приводит к значительному изменению 
.
3. Реостатное регулирование - ступенчатое, так как величина сопротивления резистора в якорной цепи допускает лишь дискретное изменение. Получение большого числа ступеней затруднено, так как требует большого количества коммутирующих аппаратов (контакторов).
4. При принятых ранее допущениях (внешний обдув) можно считать, что Мдоп = Мн на любой реостатной характеристике, так как магнитный поток неизменен.
|
|
|
5. Потери энергии при регулировании значительны и связаны с глубиной регулирования. Это непосредственно вытекает из способа регулирования: скорость изменяется за счет включения резистора - элемента, превращающего поступающую в него электрическую энергию в тепло. Найдем количественную оценку потерь мощности (энергии) при реостатном регулировании. Умножив обе части уравнения (1.3) на I, получим уравнение баланса мощностей
UI = EI+I2 R,
где UI = P1 - мощность, потребляемая из сети;
EI = Pэм - электромагнитная мощность, преобразуемая в механическую;
I2R = DP - потери мощности в якорной цепи.
Выразив U и E через магнитный поток и скорость в соответствии с (1.1) и подставив их в выражение для DP, будем иметь:
(3.19)
Этот результат - потери мощности пропорциональны относительному перепаду скорости - очень важен и, как мы увидим далее, универсален, применим к ряду других случаев.
6. Капитальные затраты на реостатное регулирование сравнительно невелики: к двигателю добавляется лишь недорогой резистор и коммутационная аппаратура.
Таким образом, реостатное регулирования координат используется в основном для механизмов, не предъявляющих жестких требований к стабильности скорости. К ним относятся, в частности, грузоподъемные механизмы, устанавливаемые в цехах промышленных предприятий. Дополнительным обстоятельством, диктующим применение этого способа регулирования, является наличие сети постоянного тока, например, в автомобилях.
|
|
|
Рассмотрим реостатный пуск на примере ДПТ НВ. На рис. 13 приведена схема силовых цепей реостатного пуска двигателя. Реостатный пуск предусматривает при подаче напряжения на якорную цепь введение добавочного сопротивления, ограничивающего величину тока якоря допустимым значением по технологическим условиям пуска. На рис. 16 приведены механические характеристики, обеспечивающие пуск двигателя. При замыкании контактора КЛ протекает ток I1 через обмотку якоря и добавочные сопротивления R1доб и R2доб, создается момент М1. Двигатель разгоняется по характеристике 1, ток снижается, и при скорости ω1 и моменте переключения M2 включается контактор КУ1, шунтируя R1доб. Двигатель переводится на характеристику 2. Ток якоря вновь увеличивается до значения I1, момент – до M1. Происходит разгон по характеристике 2 до скорости ω2, где при моменте переключения M2 включается контактор КУ2, переводя двигатель на естественную характеристику. На этой характеристике продолжается разгон до скорости ωc, где при M = Mc двигатель переходит в установившийся режим работы.
Рис. 16. Правильная пусковая диаграмма.
Правильная пусковая диаграмма строится из условия поддержания постоянства среднего пускового момента двигателя, обеспечивая равенство максимальных моментов M1 на каждой из пусковых характеристик, а также равенство моментов переключения M2 (см. рис. 16).
Рассмотрим порядок расчета правильной пусковой диаграммы аналитическим методом.
1. по заданному способу пуска (форсированный, с допустимым ускорением, нормальный) определяется момент M1 (или момент M2);
2. при ω = 0 рассчитывается R = Uн/I1, где I1 = M1/kФн;
3. разбивается Rдоб на ступени, обеспечивая правильную пусковую диаграмму.
Современные станции управления выпускают с двумя – тремя ступенями. При увеличении числа ступеней растут габариты и стоимость установки, но снизить время пуска не удается, так как каждый аппарат обладает конечным быстродействием.
При ω = ω1 токи якоря
, 
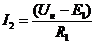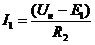, тогда 
.
При ω = ω2 токи якоря
, 
, тогда 
.
В общем случае и при большем числе ступеней отношение токов и сопротивлений остается величиной постоянной
,
откуда 
. Необходимо убедиться, что M2 ≥ 1,2∙Mc.
Таким образом, для разбиения Rдоб = R1 на ступени задаемся током I1, числом ступеней m и определяем λ = I1/I2. По величине λ рассчитываем полные сопротивления на пусковых характеристиках.
Сопротивления ступеней:
; 
.
Расчет правильной пусковой диаграммы можно выполнить графическим методом. Отметим, что для двигателей с нелинейными механическими характеристиками графический метод является наиболее удобным. Расчет графическим методом проще вести в относительный единицах (о.е.).
1. Строится естественная механическая характеристика (рис. 17).
2. Задаемся токами I1 и I2 (или моментами M1 и M2).
3. Методом подбора строится правильная пусковая диаграмма таким образом, чтобы переход на естественную характеристику совпал с моментом M1. Если моменты не совпали, вновь задаются моментом переключения M2 и повторяют построение.
4. После построения правильной пусковой диаграммы при M = 1 измеряют отрезки, пропорциональные добавочным сопротивлениям в долях от известной величины сопротивления якоря
ab ≡ rя, bc ≡ R3доб, cd ≡ R2доб, de ≡ R1доб,
и рассчитывают сопротивления ступеней
, 
, 
.
Рис. 17. Расчет правильной пусковой диаграммы графическим методом.
Дата добавления: 2018-02-15; просмотров: 1030; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!