Уравнение механической характеристики ДПТ с НВ

⇐ ПредыдущаяСтр 3 из 6Следующая ⇒

С учетом третьего уравнения в (1.1) уравнение (1.2) можно переписать в виде зависимости - которая представляет собой механическую характеристику ДПТ:

(1.7)

Данное уравнение определяет зависимость угловой скорости вращения от момента на валу двигателя. Т.к. в статике вращающий момент равен моменту сопротивления 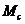на налу ДПТ, то это уравнение определяет зависимость от .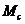

Следует отметить, что величина электромагнитного момента превышает выходной момент на валу на величину, соответствующую потерям в стали и механическим потерям от трения, но в большинстве практических расчетов указанными потерями можно пренебречь.

Коэффициент пропорциональности можно считать постоянным для тех ДПТ с НВ, у которых имеются компенсационные обмотки или в случае, когда можно пренебречь влиянием реакции якоря на величину . В общем же случае влияние поперечной реакции якоря на величину магнитного потока ведет к нарушению линейности механической характеристики по мере увеличения тока.

Графическое изображение механической характеристики

Из выражения (1.7) следует, что графически механическая характеристика ДПТ с НВ может быть представлена прямой линией с двумя характерными точками - скоростью холостого хода w₀и моментом короткого замыкания 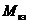, который также называется пусковым. Величина 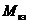определяется по формуле

(1.8)

C введением добавочного сопротивления в цепь якоря жесткость механических характеристик также падает, что с успехом используется при регулировании скорости вращения ДПТ.

По аналогии с электромеханическими характеристиками различают естественную и искусственные механические характеристики.

Жесткость естественной характеристики определяется только сопротивлением якорной цепи двигателя:

или . (1.9)

Снижение скорости под нагрузкой объясняется следующим. При увеличении момента сопротивления механизма угловая скорость начинает снижаться. В результате уменьшается ЭДС Е согласно системе (1.1). Ток якоря при этом увеличивается. Соответственно возрастает момент двигателя. Этот процесс продолжается до тех пор, пока момент двигателя не сравняется с моментом сопротивления. После достижения равенства М=М_с наступит новый установившийся режим с меньшей угловой скоростью .

При инженерных расчетах коэффициенты, входящие в уравнения характеристик двигателя, могут быть определены через номинальные параметры двигателя, приводимые в каталогах. При номинальном магнитном потоке

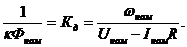                                          (1.10)

Здесь коэффициент К_д- коэффициент передачи двигателя, его размерность 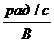. С использованием этого понятия уравнения (1.2), (1.7) могут быть переписаны в виде:

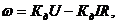                                                                  (1.11)

                                                               (1.12)

В этих уравнениях, как и в (1.2, 1.7), первый член представляет собой угловую скорость идеального холостого хода, а второй – падение скорости от нагрузки:

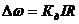,                                       (1.13)

или

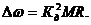                                                       (1.14)

Дата добавления: 2018-02-15; просмотров: 1650; Мы поможем в написании вашей работы!
Поделиться с друзьями:

⇐ Предыдущая 1 234 5 6 Следующая ⇒

Мы поможем в написании ваших работ!