Проверка гипотезы о существенности расхождения средних (долей)
К расчетам ошибок случайной выборки прибегают в тех случаях, когда необходимо сравнить между собой средние величины данного признака по двум совокупностям, т. е. определить, существенно ли расхождение между двумя выборочными средними или несущественно; следовательно, превосходит или не превосходит максимальной величины случайного расхождения, которое можно ожидать с определенной вероятностью. Другими словами, можно ли считать, что генеральные средние в двух подгруппах одинаковы и эти подгруппы можно объединить в одну группу и характеризовать последнюю общей средней?
Для ответа на вопрос сначала определяют среднюю (стандартную) случайную ошибку разности двух выборочных средних ( 
); для двух независимых выборок она определяется по формуле:
,
где 
—выборочные дисперсии соответственно в первой и во второй выборках;
— стандартная ошибка средней соответственно в первой и во
второй выборках;
— количество наблюдений соответственно в первой и во второй выборках.
Затем сопоставляют разность двух выборочных средних с величиной средней квадратической ошибки этих средних:
.
По таблице Лапласа определяют по полученному значению t соответствующую вероятность (Р) (см. приложение 3). Если вероятность значительна, то нулевая гипотеза, т. е. предположение об отсутствии существенного различия, не опровергается.
Получить ответ на выдвинутую нулевую гипотезу можно иначе. Зная величину ошибки разности выборочных двух средних, можно с заданной вероятностью указать предел возможных расхождений двух выборочных средних. Если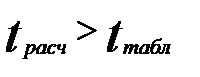 
при определенной заданной доверительной вероятности, то это свидетельствует о том, что нулевая гипотеза не подтверждается.
|
|
|
При малом объеме выборок используется распределение Стьюдента (см. приложение 4).
Проверка гипотезы о существенности расхождения двух выборочных долей осуществляется аналогично.
Ошибка разности двух долей при справедливости нулевой гипотезы исчисляется по формуле:
.
Расчетное значение t-критерия:
При заданной доверительной вероятности определяется 
. Если 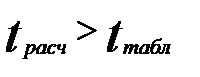, то это говорит о том, что нулевая гипотеза не подтверждается.
Элементы дисперсионного анализа
Дисперсионный анализ является одним из методов изучения влияния одного или нескольких факторных признаков на результативный признак. В зависимости от количества факторов дисперсионный анализ подразделяется на однофакторный и многофакторный. Ниже рассмотрено применение дисперсионного анализа для случая однофакторного комплекса.
В основе дисперсионного анализа лежит расчленение общей вариации изучаемого признака по источникам ее происхождения на два вида вариации:
|
|
|
• систематическую вариацию, которая обусловлена изменением признака-фактора;
• остаточную (случайную) вариацию, обусловленную действием прочих, случайных, не связанных с данным фактором обстоятельств.
Для разграничения этих вариаций всю совокупность наблюдавшихся единиц разбивают на группы (классы) по факторному признаку и исчисляют средние результативного признака по группам.
Групповые средние —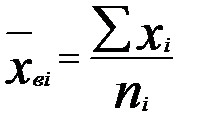 
;
общая средняя —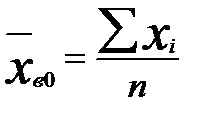 
,
где 
— индивидуальные значения признака в группе;
- число единиц, входящих в группу;
п— общее число наблюдений.
Если сравнение групповых средних показывает определенное различие в их уровне, то необходимо установить, является ли это различие существенным и вызвано ли оно влиянием признака- фактора.
Для ответа на поставленный вопрос определяют два показателя дисперсии:
1) показатель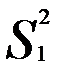 
, характеризующий вариацию групповых средних вокруг общей средней (межгрупповая дисперсия);
2) показатель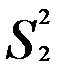 
, отражающий остаточную, внутригрупповую дисперсию. Полученные показатели сравнивают, получая фактическое дисперсионное отношение:
.
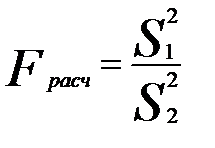При дисперсионном анализе межгрупповую 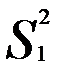и внутригрупповую 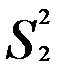дисперсии определяют путем деления суммы квадратов отклонений на соответствующее число степеней свободы:
|
|
|
,
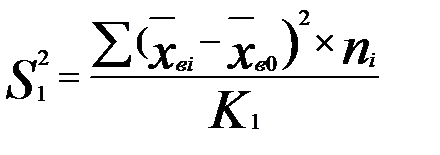где 
— число единиц в группе;
;
m — число групповых средних (число выделенных групп по признаку- фактору);
;
.
По таблице F-распределения Р. Фишера (см. приложение 5) при определенном уровне значимости (или доверительной вероятности) и числе степеней свободы { 
определяется табличное дисперсионное отношение ( 
).
Если 
, то следует считать, что гипотеза о влиянии признака-фактора не опровергается.
Дата добавления: 2018-02-15; просмотров: 867; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!