Формулы ошибок типической выборки
Как видно из приведенных выше формул, величина стандартной ошибки типической выборки зависит только от точности определения групповых средних, т. е. от величины внутригрупповых дисперсий. Согласно правилу сложения дисперсий общая дисперсия слагается из межгрупповой дисперсии и средней из внутригрупповых дисперсий. Отсюда следует, что ошибка типической случайной выборки меньше, чем ошибка простой случайной выборки.
Предельная (максимально возможная) ошибка типической выборки:
Необходимый объем выборки определяется на основе формулы и величины допустимой ошибки.
Серийная выборка
Сущность серийной выборки заключается в том, что вместо случайного отбора единиц совокупности осуществляется отбор групп (серий, гнезд). Внутри отобранных серий производится сплошное наблюдение. Серии (гнезда) состоят из единиц, связанных между собой или территориально, или организационно, или, наконец, во времени. Отбор серий может производиться в порядке повторного и бесповторного отбора. Серии могут быть равновеликими и неравновеликими. На практике чаще применяется серийный отбор с равными сериями.
Стандартная ошибка при равновеликих сериях определяется по формулам, представленным в табл. 6.4.
Таблица 6.4
В табл. 6.4 приняты следующие условные обозначения:
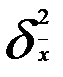— межгрупповая выборочная дисперсия средней:
,
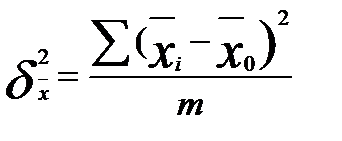где 
— средний уровень признака в серии;
|
|
|
— средний уровень признака для всей выборочной совокупности;
m — число равных серий в выборочной совокупности;
М — число равных серий в генеральной совокупности.
- межгрупповая выборочная дисперсия доли:
,
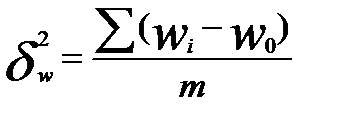где 
— доля единиц, обладающих данным признаком в серии;
— доля единиц, обладающих данным признаком во всей выборочной совокупности.
Ошибка серийной выборки больше, чем при любом другом способе отбора. Тем не менее, серийный отбор широко применяется на практике, что объясняется его организационными преимуществами.
Механическая выборка
Механическая выборка заключается в отборе единиц из генеральной совокупности через равные промежутки из определенного расположения их в генеральной совокупности (по алфавиту, в пространстве, последовательности появления во времени).
При организации механического отбора возникают две задачи:
• определение «шага отчета» (расстояния между отбираемыми единицами);
• выбор единицы, с которой надо начинать отчет.
«Шаг отчета» определяется путем деления численности генеральной совокупности на численность выборочной совокупности: 
.
Выбор начала отчета рекомендуется производить путем случайного отбора из единиц первого интервала — первого «шага отчета». Механический отбор может осуществляться в самом процессе наблюдения, и его удобно применять тогда, когда выборочно наблюдается масса постепенно возникающих перед наблюдателем единиц (например, производят проверку каждой 10-й, 20-й и т. д. детали, обработанной на станке).
|
|
|
Если в генеральной совокупности единицы располагаются случайным образом по отношению к изучаемому признаку, то механический отбор можно рассматривать как разновидность случайного бесповторного отбора; поэтому для оценки ошибки механической выборки применяются формулы случайной бесповторной выборки:
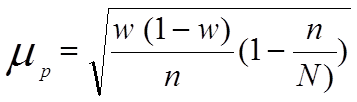
Комбинированная выборка
Комбинированная выборка предполагает использование нескольких способов выборки. Можно комбинировать, например, серийную выборку и случайную. В этом случае, разбив генеральную совокупность на серии (группы) и отобрав нужное число серий, производят случайную выборку единиц в серии. Такая комбинированная выборка может быть повторной (для групп и единиц) и бесповторной.
Средняя ошибка комбинированной выборки определяется по формулам (условные обозначения даны раньше):
при повторном отборе - 
;
|
|
|
при бесповторном отборе –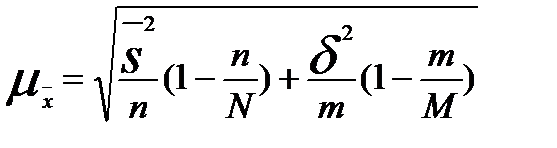 
.
Многоступенчатая выборка
Многоступенчатая выборка предполагает извлечение из генеральной совокупности сначала укрупненных групп единиц, затем групп, меньших по объему, и так до тех пор, пока не будут отобраны те группы (серии) или отдельные единицы, которые будут подвергнуты наблюдению. Выборка может быть двухступенчатой, когда генеральная совокупность разбивается на группы и производится отбор групп, а затем внутри групп — отбор единиц наблюдения. На обеих ступенях отбор может вестись в случайном порядке.
В отличие от типического отбора, где отбор производится из всех без исключения групп, при многоступенчатом отборе производится отбор самих групп, и, следовательно, не все они попадают в выборку.
Число ступеней отбора может быть и более двух. Если число ступеней отбора больше двух, то средняя ошибка выборки определяется по формуле:
,
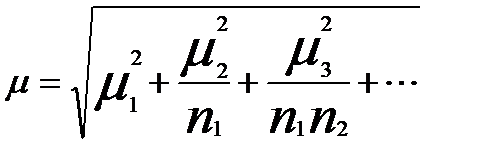где 
— средние ошибки выборки на отдельных ступенях отбора;
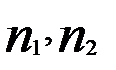- численность выборок на соответствующих ступенях.
Многофазная выборка
При многофазной выборке выборочные совокупности образуются так, что одни сведения собираются от всех единиц отбора, затем отбираются еще некоторые единицы, которые и обследуются по более широкой программе. Расчет ошибки многофазной выборки производится для каждой фазы в отдельности.
|
|
|
Малые выборки
Выборки, при которых наблюдением охватывается небольшое число единиц (n< 30), принято называть малыми выборками. Они обычно применяются в том случае, когда невозможно или нецелесообразно использовать большую выборку (исследование качества продукции, если это связано с ее разрушением, в частности на прочность, на продолжительность срока службы и т. д.).
Предельная ошибка малой выборки определяется по формуле:
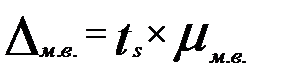
Средняя (стандартная) ошибка малой выборки:
,
где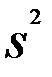 
- дисперсия малой выборки;
,
где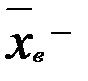 
среднее значение признака по выборке;
-число степеней свободы;
-коэффициент доверия малой выборки, зависящий не только от заданной доверительной вероятности, но и от численности единиц выборки.
Вероятность того, что генеральная средняя находится в определённых границах, определяется по формуле:
,
где 
- значение функции Стъюдента.
Для расчета коэффициента доверия 
определяют значение функции по формуле:
,
где Р — величина доверительной вероятности.
Затем по таблице распределения Стьюдента (см. приложение 4 Практикума) в зависимости от значения функции и числа степеней к определяют значение t.
Функция используется также для определения вероятностей того, что фактическое нормированное отклонение 
не превзойдет или превзойдет табличное значение.
Вероятность того, что фактическое отношение (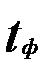 
) не превзойдет по абсолютной величине табличное значение (t), определяется по формуле:
.
Вероятность того, что фактическое отношение превзойдет по абсолютной величине табличное значение:
.
Метод моментных наблюдений
Метод моментных наблюдений применяется для получения структуры затрат рабочего времени, характеристики использования оборудования. Сущность метода состоит в периодической фиксации состояния наблюдаемых единиц в заранее установленные или случайно выбранные моменты времени. При этом заранее составляется перечень всех возможных состояний процесса или видов затрат времени. По окончании наблюдения исследователь подсчитывает долю отметок о каждом состоянии или виде затрат времени в общем числе наблюдений; при этом считается, что доля времени, затраченного на данный вид работы, может быть оценена с помощью доли моментов, когда выполнялась эта работа, в общем числе наблюдений.
Например, при изучении использования фонда рабочего времени рабочими механического цеха проведено моментное выборочное обследование. При регистрации состояния занятости 20 рабочих (работал или не работал) было выполнено 6 обходов рабочих мест и 120 наблюдений (20 х 6); из общего числа наблюдений 102 отметки состояния «работа» и 18 отметок состояния «простой».
Из полученной информации была определена доля потерь рабочего времени:
.
Средняя ошибка доли определяется по формуле простой случайной выборки:
,
где w - доля отметок о данном состоянии процесса;
п — количество моментов наблюдения.
Предельная ошибка 
.
При подготовке к проведению моментных наблюдений необходимо разработать перечень различных возможных состояний наблюдаемых объектов. Степень детализации элементов затрат рабочего времени или причин простоев и видов работы оборудования зависит от поставленной задачи. Целесообразно выделять только те элементы затрат времени или причины простоев, которые имеют удельный вес не менее 5%, поскольку в противном случае резко увеличивается необходимый объем наблюдений.
Для определения численности моментов наблюдения применяется следующая формула:
Значение коэффициента кратности (t) определяется в зависимости от принятой вероятности Р. Для стабильного производственного процесса принимается t = 2 (вероятность Р = 0,954), для нестабильного производственного процесса t = 3 (вероятность Р = 0,997).
Величина ошибки выборки ( 
) устанавливается исследователем; ее значение не должно превышать 5%.
Величина w берется из ранее проводимых наблюдений; однако если ранее подобные наблюдения не проводились и величина w неизвестна, то ориентируются на наибольшую дисперсию, когда w = 0,5:[w (1 — w) = 0,25].
После определения числа наблюдений устанавливается необходимое число обходов как частное отделения количества наблюдений на число рабочих мест, подлежащих обследованию.
Следующим этапом является составление графика проведения наблюдения. Наблюдение за состоянием процесса осуществляется через определенные промежутки времени. Примомент ном наблюдении со случайным отбором моменты отбираются при помощи таблиц случайных чисел, что целесообразно в тех случаях, когда наблюдение для объекта должно быть неожиданным.
Дата добавления: 2018-02-15; просмотров: 1165; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!