Типическая (или районированная) выборка
УТВЕРЖДАЮ
Заведующий кафедрой
___к.э.н., доцент______
(уч. степень, уч. звание)
Н.В. Ширкунова
(подпись, инициалы, фамилия)
«30» августа 2012 г.
ПЛАН
Чтения лекции №6
по дисциплине Теория статистики
Тема:«Выборочное наблюдение»
(наименование темы)
Цельзанятия:ознакомить студентов со способами отбора ивидами выборочного наблюдения и с элементами дисперсионного анализа.
Литература по теме:
1. а) основная __1. Елисеева И.И. Статистика. – М., 2010.
2. Ефимова М.Р. и др. Практикум по общей теории статистики: Учебное пособие / М.Р. Ефимова, О.И. Гончаренко, Е.В. Петрова – М.: Финансы и статистика, 2004.
3. Шмойлова Р.А. Теория статистики. – М.: Финансы и статистика, 2009.
| №№ п.п. | Содержание занятия | Отводимое учебное время, мин. | Применяемые наглядные пособия и ТСО |
| 1 2 | Организационная часть - проверить наличие студентов* Вводная часть (вступительное слово) - кратко напомнить материал предыдущего занятия; - объявить тему лекции; - довести учебные вопросы; - определить место темы в учебном курсе, указать связь с предыдущими темами и междисциплинарные связи; - отметить актуальность темы и ее практическое значение; - довести цель занятия; - сообщить литературныеисточники по теме занятия. | 2 3 | |
| 3 | Основная часть (учебные вопросы) Излагаются вопросы (проблемы), изучаемые на лекции: 1.Понятие о выборочном наблюдении: -простая случайная выборка; -типическая (или районированная) выборка; - серийная выборка; -механическая выборка; -комбинированная выборка; -многоступенчатая выборка; - многофазная выборка; - малые выборки. 2.Метод моментных наблюдений. 3.Проверка гипотезы о существенности расхождения средних (долей. 4.Элементы дисперсионного анализа. | 30 20 20 10 | PowerPoint |
| 4 | Заключительная часть - сделать выводы по теме лекции; - ответить на вопросы студентов; - дать задание на самостоятельную работу; - объявить тему следующего занятия. | 5 |
|
|
|
Преподаватель: профессор Новиков В.В._______
(должность, подпись, инициалы, фамилия)
«30» августа 2012 г.
Кафедра таможенной статистики
УТВЕРЖДАЮ
Заведующая кафедрой
|
|
|
Н.В. Ширкунова
ЛЕКЦИЯ № 6
на тему: «Выборочное наблюдение»
Дисциплина: Теория статистики
Автор: к.т.н., с.н.с. Новиков В.В.
Москва
2012
ЛЕКЦИЯ № 6
Выборочное наблюдение
Понятие о выборочном наблюдении
Наиболее совершенным и научно обоснованным способом несплошного наблюдения является выборочное наблюдение, получившее в настоящее время широкое применение в работе органов государственной статистики, научно-исследовательских лабораторий, институтов, предприятий. Его использование позволяет лучше организовать наблюдение, обеспечивает быстроту проведения, экономию труда и средств на получение и обработку информации.
Выборочное наблюдение при строгом соблюдении условий случайности и достаточно большой численности отобранных единиц репрезентативно (представительно); по результатам изучения определенной части единиц с достаточной для практики степенью точности можно судить о всей совокупности. Однако вычисленные по материалам выборочного наблюдения статистические показатели не будут точно совпадать с соответствующими характеристиками для всей совокупности (генеральной совокупности). Величина этих отклонений называется ошибкой наблюдения, которая складывается из ошибок двоякого рода: ошибки регистрации (точности) и ошибки репрезентативности.
|
|
|
Ошибки регистрации свойственны любому наблюдению (сплошному и несплошному). Они вызываются несовершенством измерительных приборов, недостаточной квалификацией наблюдателя, неточностью подсчетов и т. п. Однако при выборочном наблюдении они значительно меньше, так как в этом случае используются более квалифицированные и подготовленные кадры.
Ошибки репрезентативности свойственны только несплошным наблюдениям. Они характеризуют размер расхождений между величинами показателя, полученного в выборочной и генеральной совокупности в условиях одинаковой точности единичных наблюдений. Ошибки репрезентативности могут быть систематическими и случайными. Систематические ошибки возникают при нарушении установленных правил отбора единиц. Случайные ошибки репрезентативности обязаны своим возникновением недостаточно равномерным представлением в выборочной совокупности различных категорий единиц генеральной совокупности.
Величина случайной ошибки определяет надежность данных выборочного наблюдения, их пригодность для суждения о генеральной совокупности. При помощи формул теории вероятностей можно рассчитать возможную максимальную случайную ошибку — вероятный (стохастический) предел ошибки.
|
|
|
Максимально возможная ошибка — это такая величина откло-нения выборочной средней (доли) от генеральной, вероятность превышения которой вследствие случайных причин в условиях данной выборки очень мала.
Величина случайной ошибки репрезентативности зависит от:
• степени вариации изучаемого признака в генеральной совокупности;
• способа формирования выборочной совокупности;
• объема выборки.
По степени охвата единиц исследуемой совокупности различают большие и малые выборки. От объема выборки зависит не только величина тех предельных значений, за которые с данной вероятностью не выйдет ошибка выборочной средней, но и способы определения этих пределов. К безусловно малым относятся выборки объемом менее 30 единиц.
По способу формирования выборочной совокупности различают следующие виды выборочного наблюдения: простая случайная (собственно случайная) выборка, типическая (районированная, или стратифицированная), серийная, механическая, комбинированная, ступенчатая, многофазная.
Совокупность единиц, из которых производится отбор, приято называть генеральной совокупностью. Совокупность отобранных единиц из генеральной совокупности называется выборочной совокупностью.
N — объем генеральной совокупности (число входящих в нее единиц);
п— объем выборочной совокупности (число единиц, попавших в выборку);
 — генеральная средняя (среднее значение признака в генеальной совокупности);
— генеральная средняя (среднее значение признака в генеальной совокупности);

 — выборочная средняя (среднее значение признака в выборочной совокупности);
— выборочная средняя (среднее значение признака в выборочной совокупности);
р— генеральная доля (доля единиц, обладающих данным признаком в генеральной совокупности);
w — выборочная доля (доля единиц, обладающих данным признаком в выборочной совокупности);
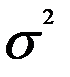 — генеральная дисперсия (дисперсия признака в генеральной совокупности);
— генеральная дисперсия (дисперсия признака в генеральной совокупности);
 — выборочная дисперсия (дисперсия признака в выборочной совокупности);
— выборочная дисперсия (дисперсия признака в выборочной совокупности);
 — среднее квадратическое отклонение признака в генеральной совокупности;
— среднее квадратическое отклонение признака в генеральной совокупности;
S — среднее квадратическое отклонение признака в выборочной совокупности.
Простая случайная выборка
При простой случайной выборке отбор единиц в выборочную совокупность производится непосредственно из всей массы единиц генеральной совокупности в форме случайного отбора, при котором каждой единице генеральной совокупности обеспечивается одинаковая вероятность (возможность) быть выбранной. Единица отбора совпадает с единицей наблюдения. Случайный отбор осуществляется путем применения жеребьевки (лотереи) или путем использования таблиц случайных чисел.
Случайный отбор может быть проведен в двух формах: в форме возвратной (повторной) выборки и в форме безвозвратной (бесповторной) выборки. При повторном отборе вероятность попадания каждой единицы генеральной совокупности остается постоянной, так как после отбора какой-то единицы она снова возвращается в генеральную совокупность и может быть выбранной. При бесповторном отборе выбранная единица не возвращается в генеральную совокупность и вероятность попадания отдельных единиц в выборку все время изменяется (для оставшихся единиц она возрастает).
Применение простой случайной повторной выборки на прак-тике весьма ограниченно; обычно используется бесповторная выборка.
Теорема Чебышева утверждает принципиальную возможность определения генеральной средней по данным случайной повтор-ной выборки. Теорема Чебышева дополняется теоремой Ляпунова, которая позволяет рассчитать максимальную ошибку выборочной средней при данном достаточно большом числе независимых наблюдений. Согласно этой теореме при достаточно большом числе независимых наблюдений в генеральной совокупости с конечной средней и ограниченной дисперсией вероятность того, что расхождение между выборочной и генеральной средней (  ) не превзойдет по абсолютной величине некоторую величину
) не превзойдет по абсолютной величине некоторую величину 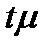 , равна интегралу Лапласа. Это можно записать так:
, равна интегралу Лапласа. Это можно записать так:

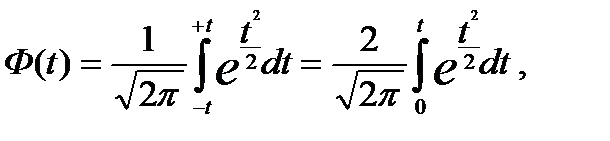
где  — интеграл Лапласа (удвоенная нормированная функция Лапласа).
— интеграл Лапласа (удвоенная нормированная функция Лапласа).
Величина 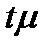 , обозначаемая
, обозначаемая  , называется предельной ошибкой выборки. Следовательно,
, называется предельной ошибкой выборки. Следовательно,
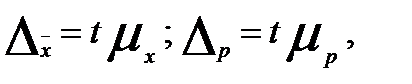
где  — предельная (максимально возможная) ошибка средней;
— предельная (максимально возможная) ошибка средней;
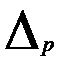 —предельная (максимально возможная) ошибка доли;
—предельная (максимально возможная) ошибка доли;
 — величина средней квадратической стандартной ошибки (стандартная или средняя ошибка);
— величина средней квадратической стандартной ошибки (стандартная или средняя ошибка);
t — коэффициент кратности средней ошибки выборки, зависящий от вероятности, с которой гарантируется величина предельной ошибки.
В зависимости от принятой вероятности Р определяется значение коэффициента кратности (t) по удвоенной нормированной функции Лапласа (см. приложение 3).
Величина средней (стандартной) ошибки в условиях большой выборки (п> 30) рассчитывается по известным из теории вероятностей формулам:
а) при случайной повторной выборке:

б) при случайной бесповторной выборке:

При расчете ошибок возникает существенное затруднение: величины  и р по генеральной совокупности неизвестны. Эти величины в условиях большой выборки заменяют величинами
и р по генеральной совокупности неизвестны. Эти величины в условиях большой выборки заменяют величинами  (выборочная дисперсия) и w (выборочная доля), рассчитанными по выборочным данным. В табл. 6.1 приведены формулы расчета ошибок простой случайной выборки.
(выборочная дисперсия) и w (выборочная доля), рассчитанными по выборочным данным. В табл. 6.1 приведены формулы расчета ошибок простой случайной выборки.
Таблица 6.1
Формулы ошибок простой случайной выборки
Формулы предельной ошибки позволяют решать задачи трех видов:
1. Определение пределов генеральных характеристик с заданной степенью надежности (доверительной вероятностью) на основе показателей, полученных по данным выборки.
Доверительные интервалы для генеральной средней:
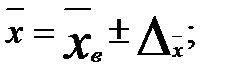

Доверительные интервалы для генеральной доли:

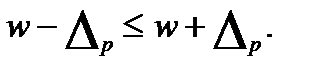
2. Определение доверительной вероятности того, что генеральная характеристика может отличаться от выборочной не более чем на определенную заданную величину.
Доверительная вероятность является функцией от t, определяемой по формуле:

По величине t определяется доверительная вероятность (приложение 3 Практикума).
3. Определение необходимого объема выборки, который с практической вероятностью обеспечивает заданную точность выборки.
Для расчета объема выборки необходимо иметь следующие данные:
а) размер доверительной вероятности (Р);
б) коэффициент t, зависящий от принятой вероятности (определяется по приложению 3 Практикума);
в) величину  (или pq) в генеральной совокупности; они заменяются величинами, полученными в предшествующих обследованиях или при пробных выборках [
(или pq) в генеральной совокупности; они заменяются величинами, полученными в предшествующих обследованиях или при пробных выборках [ 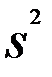 или w(1—w)];
или w(1—w)];
г) величину максимально допустимой ошибки (  или
или  );
);
д) объем генеральной совокупности (N).
Необходимый объем выборки определяется на основе допустимой величины ошибки:

В табл. 6.2 приведены формулы для расчета численности простой случайной выборки.
Таблица 6.2
Формулы для определения численности простой случайной выборки
* В случаях, когда частостьw даже приблизительно неизвестна, в расчет вводят максимальную величину дисперсии доли, равную 0,25 (если w = 0,5, то w(l— w) = 0,25).
Типическая (или районированная) выборка
В составе генеральной совокупности с различным уровнем изучаемого признака желательно обеспечить более равномерное представительство в выборочной совокупности различных типов. Эта цель достигается при применении типической (районированной, или стратифицированной) выборки. Эту выборку применяют также в целях более равномерного представления в выборке различных районов, и в этом случае ее называют районированной выборкой.
При типической выборке неоднородная генеральная совокупность подразделяется на более однородные в отношении изучаемых признаков группы (типы, районы). По каждой группе определяются ее объем (Ni,) и число подлежащих наблюдению единиц ( 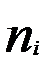 ). Отбор обследуемых единиц производится в каждой группе при помощи одного из способов случайного отбора — повторного или бесповторного.
). Отбор обследуемых единиц производится в каждой группе при помощи одного из способов случайного отбора — повторного или бесповторного.
Общее число единиц выборочной совокупности распределяется между группами пропорционально численности групп в составе генеральной совокупности. Такой отбор называется пропорциональным.
N— общая численность единиц в генеральной совокупности.
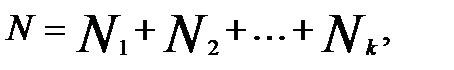
где 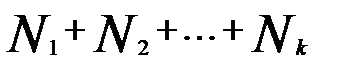 — численность отдельных групп генеральной совокупности.
— численность отдельных групп генеральной совокупности.
Объем выборки для каждой группы :

где n — общий объем выборочной совокупности;
 — удельный вес данной (i-ой) группы в генеральной совокупности;
— удельный вес данной (i-ой) группы в генеральной совокупности;

Кроме пропорционального размещения по группам численности единиц выборочной совокупности применяется так называемое оптимальное размещение, при котором число наблюдений в группе определяется по формуле:

где  —среднее квадратическое отклонение изучаемого признака в i-й группе.
—среднее квадратическое отклонение изучаемого признака в i-й группе.
Формулы для расчета ошибок типической выборки приведены в табл. 6.3. В этой таблице приняты следующие условные обозначения:
 — средняя групповая выборочная дисперсия :
— средняя групповая выборочная дисперсия :
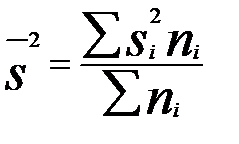 ;
;
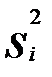 — внутригрупповая дисперсия данной (i-й) группы в выборочной совокупности;
— внутригрупповая дисперсия данной (i-й) группы в выборочной совокупности;
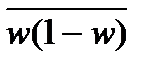 — средняя групповая выборочная дисперсия доли:
— средняя групповая выборочная дисперсия доли:
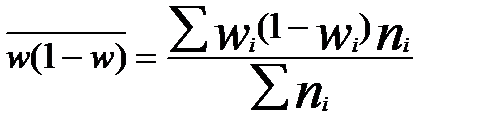 .
.
Таблица 6.3
Дата добавления: 2018-02-15; просмотров: 1195; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
