С помощью Поиска решения MS Excel
Исходные данные транспортной задачи приведены схематически: внутри прямоугольника заданы удельные транспортные затраты на перевозку единицы груза (cij), слева указаны мощности поставщиков (ai), а сверху – мощности потребителей (bj). Найти оптимальный план закрепления поставщиков за потребителями (xij).
| Мощности поставщиков | Мощности потребителей | |||
| 250 | 100 | 150 | 50 | |
| 80 | 6 | 6 | 1 | 4 |
| 320 | 8 | 30 | 6 | 5 |
| 100 | 5 | 4 | 3 | 30 |
| 50 | 9 | 9 | 9 | 9 |
В данной задаче суммарные запасы равны суммарным потребностям, т.е.
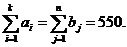
Таким образом, транспортная задача является закрытой.
Ввод условий задачи состоит из следующих основных шагов:
1. Создание формы для ввода условий задачи.
2. Ввод исходных данных.
3. Ввод зависимостей из математической модели.
4. Назначение целевой функции.
5. Ввод ограничений и граничных условий.
Изменяемые ячейки В3:Е6. В эти ячейки будет записан оптимальный план перевозок - xij.
Ввести исходные данные задачи (рис.8).
В ячейку А3 ввести формулу =СУММ(В3:Е3). Скопировать её в ячейки А4, А5, А6.
В ячейку В7 ввести формулу =СУММ(В3:В6). Скопировать её в ячейки С7, D7, E7.
Выражение для вычисления значения целевой функции в ячейке В15 получено с помощью функции СУММПРОИЗВ(В3:Е6; В10:Е13).
После вызова Поиска решения курсор подвести в поле «Установить целевую ячейку» и ввести адрес: В15. Ввести направление целевой функции «минимальному значению». Поместить курсор в поле «Изменяя ячейки». Ввести адреса изменяемых ячеек В3:Е6. Далее следует добавить ограничения.
|
|
|

Рис. 8. Создание формы для ввода условий задачи.
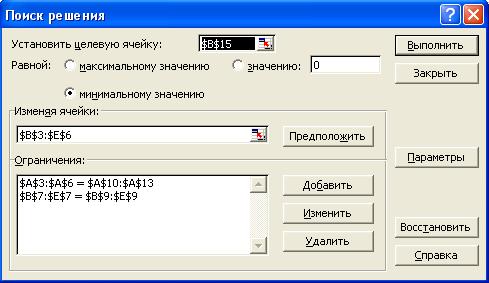
Рис. 9. Введены зависимости из математической модели.
Все грузы должны быть перевезены, т.е.

Все потребности должны быть удовлетворены, т.е.

После ввода последнего ограничения вместо добавить вести ОК. на экране появится окно Поиск решения с введёнными ограничениями (см. рис. 9).
Решение задачи
Решение задачи производится сразу же после ввода данных, когда на экране находится окно Поиск решения. С помощью окна Параметры можно вводить условия для решения оптимизационных задач. В нашей задаче следует установить флажок «неотрицательные значения» и флажок «линейная модель» (рис. 10). Нажать Ок, затем Выполнить.

Рис. 10. Установка параметров.
На экране появится диалоговое окно Результаты поиска решения и само решение. (рис.11)

Рис. 11. Оптимальный план перевозок.
В результате решения получен оптимальный план перевозок:
| Матрица перевозок (изменяемые ячейки)
| ||||||
| 80 320 100 50 | 0 200 0 50 | 0 0 100 2.13Е-14 | 80 70 0 0 | 0 50 0 0 | ||
| 550 | 250 | 100 | 150 | 50 | ||
Задачи для самостоятельного решения
Задача об ассортименте продукции


Задача о диете

Форма отчетности
Лабораторная работа сдается преподавателю за экраном монитора компьютера. Необходимо продемонстрировать результаты исследований и расчетов, показать на экране монитора ход выполнения работы, а также ответить на вопросы преподавателя.
Отчет должен содержать решение Примеров (1, 2) и Задач для самостоятельного решения (1, 2) в среде MS Excel.
Контрольные вопросы:
1. В чем состоит задача оптимизации?
2. Что такое линейное программирование?
3. Сформулируйте задачу линейного программирования.
4. Дайте определения понятиям целевая функция, ограничения, оптимальный план.
5. Для чего применяется надстройка «Поиск решения» MS Excel?
6. Опишите технологию нахождения оптимального плана при помощи MS Excel.
Дата добавления: 2018-02-15; просмотров: 1686; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
