ТЕОРИЯ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
Преподаватель: ст.преподаватель Ольга Вячеславовна Фукалова
E-mail: olga_1999em@mail.ru
Всего:
- практические занятия – 4 часа;
- лекции – 10 часов;
Контроль:
- экзамен
- контрольная работа
Элементы теории вероятностей и математической статистики
Варианты контрольной работы
Номер варианта контрольной работы, выполняемой студентом, должен совпадать с последней цифрой номера его зачетной книжки. Задание 5 смотреть в общей таблице.
Вариант 0
- Имеются 12 единиц товара в одинаковых упаковках. Известно, что в четырех из них товар первого сорта. Случайным образом отбирают 3 единицы товара. Вычислить вероятность того, что среди них: а) только упаковки с товаром первого сорта; б) ровно одна упаковка с товаром первого сорта.
- В магазин поступила обувь от двух поставщиков. Количество обуви, поступившей от первого поставщика, в 2 раза больше, чем от второго. Известно, что в среднем 20% обуви от первого поставщика и 35% обуви от второго поставщика имеют различные дефекты отделки. Из общей массы наугад отбирают одну упаковку с обувью. Оказалось, что она не имеет дефекта отделки. Какова вероятность, что её изготовил первый поставщик?
- Задан закон распределения дискретной случайной величины X:
| Х | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| Р | 0,01 | p | 0,23 | 0,2 | 0,1 | 0,1 | 0,06 |
Найти:
|
|
|
a) неизвестную вероятность p;
b) математическое ожидание М, дисперсию D и среднее квадратическое отклонение s данной случайной величины;
в) функцию распределения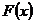 
и построить её график;
г) закон распределения случайной величины 
, если её значения заданы функциональной зависимостью 
- Известно, что в среднем 64% студентов потока выполняют контрольные работы в срок. Какова вероятность того, что из 100 студентов потока задержат представление контрольных работ:
а) 30 студентов; б) от 30 до 40 студентов?
Смотреть в общей таблице.
Вариант 1
1. В коробке 25 одинаковых по форме шоколадных конфет. Известно, что 15 штук из них сорта «Мишка на Севере», а остальные — сорта «Красная Шапочка». Случайным образом выбирают 3 конфеты. Вычислите вероятность того, что среди них: а). Все конфеты сорта «Мишка на Севере»; б). Только одна конфета этого сорта.
- В магазин поступил одноименный товар, изготовленный двумя предприятиями. С первого предприятия поступило 150 единиц, из них 30 единиц первого сорта, а со второго предприятия 200 единиц, из них 50 первого сорта. Из общей массы товара наугад извлекается одна единица товара 1-го сорта. Какова вероятность того, что она изготовлена на первом предприятии?
|
|
|
3. Задан закон распределения дискретной случайной величины X:
|
|
Найти:
a. неизвестную вероятность р;
b. математическое ожиданиеМ, дисперсию D и среднее квадратическое отклонение данной случайной величины;
в. функцию распределения 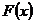и построить её график;
г. закон распределения случайной величины , если её значения заданы функциональной зависимостью 
- Известно, что в среднем 14% стаканов, изготовляемых на данном предприятии, имеет дефект. Какова вероятность того, что из 300 стаканов данной партии:
а) имеют дефект 45;
б) не имеют дефекта от 230 до 250?
Смотреть в общей таблице.
Вариант 2
1. В туристической группе 15 человек, среди которых только 5 человек хорошо говорят по-английски. В Лондоне группу случайным образом расселили в два отеля (3 человека и 12 человек соответственно). Вычислите вероятность того, что из членов группы в первом отеле: а) все туристы говорят хорошо по-английски; б). Только один турист хорошо говорит по-английски.
- Покупатель может приобрести нужный ему товар в двух магазинах. Вероятности обращения в каждый из двух магазинов зависят от их местоположения и соответственно равны 0,3 и 0,7. Вероятность того, что к приходу покупателя нужный ему товар не будет распродан, равна 0,8 для первого магазина и 0,4 для второго. Какова вероятность того, что покупатель приобретет нужный товар.
|
|
|
- Задан закон распределения дискретной случайной величины X:
| Х | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| Р | 0,0115 | 0,12 | 0,18 | 0,30 | Р | 0,12 | 0,05 |
Найти:
а) неизвестную вероятность р;
б) математическое ожидание М, дисперсию D и среднее квадратическое отклонение s данной случайной величины
в) функцию распределения 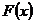и построить её график;
г) закон распределения случайной величины , если её значения заданы функциональной зависимостью 
4. Установлено, что предприятие бытового обслуживания выполняет в срок в среднем 60% заказов. Какова вероятность того, что из 150 заказов, принятых в течение некоторого времени, будут выполнены в срок:
а) 90 заказов; б) от 93 до 107 заказов?
Смотреть в общей таблице.
Вариант 3
1. К экзамену приготовлено 24 одинаковых ручки. Известно, что треть из них имеет фиолетовый стержень, остальные - синий стержень. Случайным образом отбирают три ручки. Вычислить вероятность того, что а) все ручки имеют фиолетовый стержень; б) только одна ручка имеет фиолетовый стержень.
|
|
|
2. Пассажир может приобрести билет в одной из двух касс. Вероятность обращения в первую кассу составляет 0,4, а во вторую - 0,6. Вероятность того, что к моменту прихода пассажира нужные ему билеты будут распроданы, равна 0,35 для первой кассы и 0,7 для второй. Пассажир посетил одну из касс и приобрел билет. Какова вероятность того, что он приобрел его во второй кассе?
3. Задан закон распределения дискретной случайной величины X:
| Х | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| Р | 0,05 | 0,12 | 0,13 | 0,30 | Р | 0,12 | 0,05 |
Найти:
а) неизвестную вероятность р;
б) математическое ожидание М, дисперсию D и среднее квадратическое отклонение s данной случайной величины;
в) функцию распределения 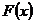и построить её график;
г) закон распределения случайной величины , если её значения заданы функциональной зависимостью 
4. Известно, что в данном технологическом процессе 10% изделий имеют дефект. Какова вероятность того, что в партии из 400 изделий:
а) не будут иметь дефекта342 изделия;
б) будут иметь дефект от 30 до 52 изделий.
Смотреть в общей таблице.
Вариант 4
1. В упаковке 12 одинаковых книг. Известно, что каждая третья книга имеет дефект обложки. Случайным образом выбирают 3 книги. Вычислите вероятность того, что среди них: а) все книги имеют дефект обложки; б). Только одна книга имеет этот дефект.
2. Два контролера производят оценку качества выпускаемых изделий. Вероятность того, что очередное изделие попадет к первому контролеру, равна 0,55; ко второму контролеру — 0,45.Первый контролёр выявляет дефект с вероятностью 0,8, а второй - с вероятностью 0,9. Вычислите вероятность того, что изделие с дефектом будет признано годным к эксплуатации.
3. Задан закон распределения дискретной случайной величины X эксплуатации.
| X | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| р | 0,42 | 0,23 | р | 0,10 | 0,06 | 0,03 | 0,01 |
Найти:
а) неизвестную вероятность р;
б) математическое ожидание М, дисперсию D и среднее квадратическое отклонение s данной случайной величины;
в) функцию распределения 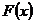и построить её график;
г) закон распределения случайной величины , если её значения заданы функциональной зависимостью 
4. По данным телеателье установлено, что в среднем 20% цветных телевизоров выходят из строя в течение гарантийного срока. Какова вероятность того, что из 225 проданных телевизоров будут работать исправно в течение гарантийного срока:
а) 164 телевизора;
б) от 172 до 184 телевизоров.
Смотреть в общей таблице.
Вариант 5
- В нижней палате парламента 40 депутатов, среди которых первая партия имеет 20 представителей, вторая — 12 представителей, третья 5 представителей, а остальные считают себя независимыми. Случайным образом выбирают трех депутатов. Вычислите вероятность того, что среди них: а). Только представители первой партии, б). Только один депутат из первой партии.
- Два специалиста ОТК проверяют качество выпускаемых изделий, причем каждое изделие с одинаковой вероятностью может быть проверено любым из них. Вероятность выявления дефекта первым специалистом равна 0,8, а вторым 0,9. Из массы проверенных изделий наугад выбрано одно, оно оказалось с дефектом. Какова вероятность того, что ошибку допустил второй контролер?
- Задан закон распределения дискретной случайной величины X:
| Х | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| Р | 0,05 | 0,12 | 0,12 | 0,30 | Р | 0,12 | 0,04 |
Найти:
а) неизвестную вероятность р;
б) математическое ожидание М, дисперсию D и среднееквадратическое отклонение s данной случайной величины;
в) функцию распределения F(x) и построить ей график;
г) закон распределения случайной величины , если её значения заданы функциональной зависимостью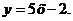 
- При оценке качества продукции было установлено, что в среднем третья часть выпускаемой фабрикой обуви имеет различные дефекты отделки. Какова вероятность того, что в партии из 200 пар, поступившей в магазин:
а) будут иметь дефекты отделки 60 пар;
б) не будут иметь дефектов отделки от 120 до 148 пар.
Смотреть в общей таблице.
Вариант 6
- В ящике 18 одинаковых бутылок пива без этикеток. Известно, что треть из них «Жигулевское». Случайным образом выбирают 3 бутылки. Вычислите вероятность того, что среди них: а) только пиво сорта «Жигулевское»; б) ровно одна бутылка этого сорта.
- В двух одинаковых коробках находятся карандаши "Конструктор". Известно, что треть карандашей в первой коробке и 0,25 во второй имеют твердость ТМ. Наугад выбирается коробка, из нее наугад извлекается один карандаш. Он оказывается твердости ТМ. Какова вероятность того, что он извлечен из первой коробки?
- Задан закон распределения дискретной случайной величины X:
| Х | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| Р | 0,05 | 0,09 | 0,15 | 0,30 | Р | 0,12 | 0,05 |
Найти:
а) неизвестную вероятность р;
б) математическое ожидание М, дисперсию D и среднее квадратическое отклонение s данной случайной величины;
в) функцию распределения F(x) и построить ей график;
г) закон распределения случайной величины , если её значения заданы функциональной зависимостью 
4. Известно, что вероятность рождения мальчика равна 0,51, а девочки 0,49. Какова вероятность того, что 300 новорожденных окажется:
а) 150 мальчиков;
б) от 150 до 200 мальчиков?
Смотреть в общей таблице.
Вариант 7
1. В студенческой группе 20 девушек. Известно, что 5 из них не любят читать детективы. Случайным образом выбирают трех девушек и дарят им по детективу. Вычислите вероятность того, что: а). Все девушки оценят этот подарок; б). Только одна девушка оценит этот подарок.
2. Товаровед плодоовощной базы определяет сорт поступившей от постоянного поставщика партии яблок. Известно, что в среднем 40% выращенного поставщиком урожая составляют яблоки первого сорта. Вероятность того, что товаровед признает первосортную партию первым сортом, равна 0,85. Кроме того, он может допустить ошибку, сочтя непервосортную партию первосортной, с вероятностью 0,2. Какова вероятность того, что он неверно установит сорт партии яблок?
3. Задан закон распределения дискретной случайной величины X:
| Х | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| Р | 0,01 | 0,15 | 0,16 | 0,30 | Р | 0,12 | 0,04 |
Найти:
а) неизвестную вероятность р;
б) математическое ожидание М, дисперсию D к среднее квадратическое отклонение s.
в) функцию распределения F(x) и построить ей график;
г) закон распределения случайной величины , если её значения заданы функциональной зависимостью 
4. Вероятность нормального расхода электроэнергии за день ша предприятии бытового обслуживания равна 0,7. Какова вероятность того, что из 90 дней предприятие нормально расходует электроэнергию:
а) в течение 60 дней; б) от 60 до 90 дней?
Смотреть в общей таблице.
Вариант 8
1. В коробке 30 одинаковых юбилейных монет. Известно, что 5 из них имеют нестандартный процент содержания золота. Случайным образом выбирают три монеты. Вычислите вероятность того, что: а). Все монеты имеют нестандартный процент содержания золота; б). Только одна монета имеет нестандартный процент содержания золота.
- Магазин получил две равные по количеству партии одноименного товара. Известночто, 25% первой партии и 40% второй партии составляет товар первого сорта. Какова вероятность того, что наугад выбранная единица товара будет не первого сорта?
- Задан закон распределения дискретной случайной величины X:
Найти:
а) неизвестную вероятность р;
б) математическое ожидание М, дисперсию D и среднее квадратическое отклонение s данной случайной величины.
в) функцию распределения F(x) и построить ей график;
г) закон распределения случайной величины , если её значения заданы функциональной зависимостью 
4. Известно, что вероятность опоздания ежедневного поезда на станцию равна 0,2. Какова вероятность того, что в течение 200 дней поезд опоздает на станцию:
а) 50 раз;
б) от100 до 150 раз?
Смотреть в общей таблице.
Вариант 9
- На витрине 32 одинаковых булочки. Известно, что среди них четверть булочек с изюмом, остальные с корицей. Случайным образом отбирают три булочки. Вычислите вероятность того, что: а). Все выбранные булочки с изюмом; б). Только одна булочка с изюмом.
- Укупорка банок производится двумя автоматами с одинаковой производительностью. Доля банок с дефектом укупорки для первого автомата составляет 1%, а для второго 0,5%. Какова вероятность того, что наугад взятая банка будет иметь дефект укупорки?
- Задан закон распределения дискретной случайной величины X:
| х | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| р | 0,08 | 0,1 | 0,14 | 0,17 | 0,1 | 0,1 | р |
Найти:
а) неизвестную вероятность р;
б) математическое ожидание М, дисперсию D и среднее квадратическое отклонение s данной случайной величины.
г) закон распределения случайной величины , если её значения заданы функциональной зависимостью 
4. Установлено, что третья часть покупателей, при посещении модного магазина приобретает себе одежду. Какова вероятность того, что из 150 посетителей магазина:
а) ровно 50 человек приобретут товар;
б) от 100 до 120 человек приобретут товар?
Смотреть в общей таблице.
Задание 5
После обработки результатов эксперимента составлена таблица, в первой строке которой указаны группы возможных значений некоторой случайной величины 
, а во второй строке – численность каждой группы значений 
. Найти объем выборки 
;относительные частоты 
, соответствующие каждой отдельной группе значений случайной величины; составить вариационный ряд распределения данной случайной величины. Найти числовые характеристики выборки: среднее арифметическое, выборочную дисперсию и среднеквадратическое отклонение (см. табл.):
| Вариант 0 | 
| 53 | 54 | 56 | 58 |
|
| 12 | 10 | 4 | 1 | |
| Вариант 1 |
| 73 | 75 | 76 | 79 |
|
| 5 | 12 | 11 | 3 |
| Вариант 2 |
| 38 | 40 | 44 | 45 |
|
| 1 | 6 | 12 | 13 | |
| Вариант 3 |
| 21 | 24 | 26 | 27 |
|
| 13 | 10 | 4 | 6 | |
| Вариант 4 |
| 27 | 30 | 33 | 40 |
|
| 5 | 6 | 11 | 10 | |
| Вариант 5 |
| 63 | 65 | 68 | 70 |
|
| 4 | 12 | 15 | 9 | |
| Вариант 6 |
| 17 | 21 | 23 | 25 |
|
| 2 | 11 | 13 | 12 | |
| Вариант 7 |
| 42 | 45 | 48 | 52 |
|
| 13 | 2 | 14 | 3 | |
| Вариант 8 |
| 56 | 60 | 63 | 65 |
|
| 11 | 10 | 3 | 7 | |
| Вариант 9 |
| 28 | 32 | 36 | 42 |
|
| 12 | 5 | 11 | 6 |
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ КВЫПОЛНЕНИЮ КОНТРОЛЬНОЙ РАБОТЫ
ЗАДАЧА 1
Наскладе университетахранится 28 одинаковых упаковок писчейбумаги. Известно, что в четырехиз нихсодержитсябумага более низкого качества. Случайнымобразомвыбирают три упаковкибумаги, Вычислить вероятность того, что среди них;
нет упаковок с бумагой более низкого качества,
есть однаупаковкатакой бумаги.
Решение. Общеечисло возможныхэлементарныхисходов для данных испытанийравно числуспособов, которымиможноизвлечь 3 упаковки бумаги из28 упаковок,то есть
= 
= 
= 
=13·9·28=3276 – числу сочетаний из 28 элементов по 3.
а)Подсчитаемчисло исходов, благоприятствующих интересующему нас событию (нет упаковокс бумагой более низкого качества). Это число исходов ровно числуспособов, которыми можно извлечь 3 упаковки бумаги из 24 упаковок (столько упаковок содержит бумагу высшего сорта), то есть
= 
= 
= 
=11·23·8=2024
искомая вероятностьравна отношению числа исходов, благоприятствующихсобытию, к числу всех элементарных исходов:
P1=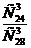 
= 
≈0,62
б) Подсчитаем число исходов,благоприятствующих данному событию (среди трех упаковокбумаги ровно 1 упаковкасодержитбумагу болеенизкого качества): две упаковкиможно выбрать из 24 упаковок: 
= 
= 
= 
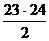=276 способами, при этом одну упаковку нужно выбирать из четырех: 
= 
= 
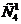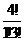=4 способами. Следовательно,число благоприятствующих исходов равно
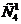· =276·4=1104
Искомая вероятность равна отношению числа исходов, благоприятствующих данному событию, к числу всехэлементарныхисходов p2= 
= 
≈0,34
Ответ: а)p1 =0,62;б) р2 =0,34.
ЗАДАЧА 2
Магазинполучает электролампочкис двух заводов,причем доля первого завода составляет 25 %. Известно,чтодоля брака на этих заводах равна соответственно5 % и 10 % от всей выпускаемой
продукции. Продавец наугад берет одну лампочку. Какова вероятность того,что она окажется бракованной?
Решение: Обозначим черезАсобытие - «лампочкаокажетсябракованной».Возможны следующие гипотезы о происхождении этой лампочки:H1-лампочка поступила с первого завода,H2-лампочка поступила со второгозавода.Так как доля первого завода составляет 25 %, то вероятности этих гипотез равнысоответственно p(H1)=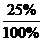 
=0,25; p(H2)= 
=0,75.
Условная вероятность того, что бракованнаялампочка выпущенапервымзаводом–p(A/H1)= 
=0,05, вторымзаводом- p(A/H2)= 
=0,10 искомую вероятностьтого, что продавец взял бракованную лампочку, находим по формуле полной вероятности
р(А) = P(H1)· p(A/H1)+P(H2)·(A/H2)=0,25·0,05+0,75·0,10=0,0125+0,075=0.0875
Ответ: р(А) = 0,0875.
Для решениязадачи5 см.[5]глава6 § 1—3, глава 7 § 1-2, глава8 § J—3.
ЗАДАЧА 3.
Задан закон распределения дискретной случайной величеныX:
|
Найти:
а) неизвестную вероятность р.
б) математическое ожидание М, дисперсию D исреднее квадратическоеотклонение σ данной случайной величены;
Решение:
а) так как сумма всех, вероятностей должна равняться единице, тополучим уравнение
0,05-p + 0,12 + 0,23-0,32 + 0,14+0,04 = 1.
Отсюда р+0,9 = 1и р=0,1.
б)Математическое ожидание М это сумма всех произведенийзначенийслучайной величины на их вероятности:
М = (-4)·0,05+(-2)·0,1 + 0·0,12 + 2·0,23 + 4·0,32 + 6·0,14 + +8·0,04-0,2-0,2+0 + 0,46 + 1,28 + 0,84 + 0.32 = -0,4 + 2,9 = 2,5.
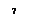Дисперсия D=∑(x1)2·p1-M2=
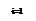
=(-4)·0.05+(-2)2·0,1+02·0,12+22·0,23+42·0,32+62·0,14+82·0,04-(2,5)2=
=0,8+0+0,92+5,12+5,04+2,56-6,25=8,59
Среднее квадратическое отклонение σ = 
= 
≈2,9
в) Если 
Если 
Если 
Если 
Если 
Если 
Если 
Если 
Итак, функция распределения может быть записана так:
График этой функции приведен на рисунке:
г) Сначала найдем значения случайной величины .
По условиям задачи 
Поэтому 
Составим таблицу вида:
| Y | 7 | 3 | -1 | 3 | 7 | 11 | 15 |
| 0,05 | 0,1 | 0,12 | 0,23 | 0,32 | 0,14 | 0,04 |
Чтобы получить закон распределения случайной величины необходимо:
1) рассмотреть её значения;
2) сложить вероятности, соответствующие совпадающим значениям данной таблицы.
Итак, закон распределения случайной величины :
| Y | -1 | 3 | 7 | 11 | 15 |
| P | 0,12 | 0,33 | 0,37 | 0,14 | 0,04 |
ЗАДАЧА 4.
Известно, что вероятность положительного исхода некоторого опыта равна 0,125. Найдите вероятность того, что в серии из 128 опытов положительный исход произойдет
а) в 20 опытах
б) от 12 до 20 опытов.
Решение:
а) воспользуемся локальной теоремой Лапласа. Вероятность того, что в 
испытаниях, в каждом из которых вероятность появления события равна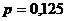 
,равна 
раз (безразлично, в какой последовательности) приближенно равна
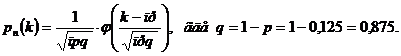
Так как 
.
Значение функции 
находим в таблице: 
Итак, 
Отметим, что таблица функции 
приведена только для положительных значений. Если же значение х получилось отрицательным, точки знак минус можно просто опустить в силу четности функции .
б) воспользуемся интегральной теоремой Лапласа. Вероятность того, что в независимых испытаниях событие наступит от 
до 
раз приближенно равна
Так как 
,
где 
Значение функции 
также находим в специальной таблице. В таблице 
. Для отрицательных значений х используют эту же таблицу, учитывая, что является нечетной функцией, то есть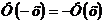 
. Итак, 
Отсюда
Ответ: 
ТЕОРИЯ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
Дата добавления: 2018-02-15; просмотров: 2791; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!