Преподаватель: ст.преподаватель Ольга Вячеславовна Фукалова
E-mail: olga_1999em@mail.ru
Всего
- практические занятия – 5 часа;
- лекции – 9 часов;
Контроль:
- контрольная работа
- экзамен
ВОПРОСЫ К ЭКЗАМЕНУ:
1. Кривые второго порядка: окружность, эллипс.
2. Кривые второго порядка: гипербола, парабола.
3. Различные уравнения прямой на плоскости. Основные задачи.
4. Различные уравнения прямой в пространстве. Основные задачи.
5. Различные уравнения плоскости в пространстве. Основные задачи.
6. Векторы. Действия над векторами. Координаты вектора. Базис и ранг системы векторов.
7. Скалярное произведение векторов. Ортобазис, ортонормированный базис.
8. Линейно зависимые и линейно независимые системы векторов.
9. Коллинеарные и компланарные векторы.
10. Векторное произведение векторов.
11. Смешанное произведение векторов.
12. Системы линейных неравенств с двумя переменными.
13. Основная задача линейного программирования (ЛП). Геометрический метод решения задач ЛП с двумя переменными.
14. Транспортная задача.
15. Понятие экономико-математической модели. Этапы создания модели. Классификация ЭММ.
16. Действия, предполагаемые при построении ЭММ. Особенности ЭММ.
17. Закон Ирвинга Фишера.
18. Детерминированная однопродуктовая модель управления текущими запасами.
19. Эластичность спроса.
20. Игровые модели.
21. Задача управления запасами при случайном спросе.
22. Основные понятия и методы нелинейного программирования.
23. Понятие о динамическом программировании и его методах.
КОНТРОЛЬНЫЕ ЗАДАНИЯ:
ЗАДАНИЕ 1
Даны вершины треугольника 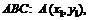

 .
.
Найти:
1. Уравнения всех сторон треугольника в общем виде, привести их к уравнению с угловым коэффициентом, построить.
2. Уравнение высоты 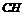 , построить.
, построить.
3. Уравнение медианы  построить.
построить.
4. Точку  пересечения высоты
пересечения высоты 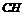 и стороны
и стороны  .
.
5. Расстояние от точки  до прямой
до прямой 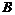 .
.
6. Периметр треугольника 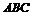 .
.
7. Угол между прямыми  и
и  .
.
| ВАРИАНТ | А | В | С |
| 1 | (– 2; 4) | (3; 1) | (10; 7) |
| 2 | (– 3; – 2) | (14; 4) | (6; 8) |
| 3 | (1; 7) | (– 3; –1) | (11; – 3) |
| 4 | (1; 0) | (– 1; 4) | (9; 5) |
| 5 | (1; – 2) | (7; 1) | (3; 7) |
| 6 | (– 2; – 3) | (1; 1) | (6; 1) |
| 7 | (– 4; 2) | (– 6; 6) | (6; 2) |
| 8 | (4; – 3) | (7; 3) | (1; 10) |
| 9 | (4; – 4) | (8; 2) | (3; 8) |
| 10 | (– 3; – 3) | (5; 27) | (7; 7) |
ЗАДАНИЕ 2
Привести уравнение кривой второго порядка к каноническому виду, определить геометрический образ и построить кривую.
ВАРИАНТ 1
а) 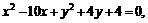
б) 
в) 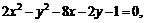
г) 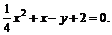
ВАРИАНТ 2
а) 
б) 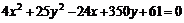 ,
,
в)  ,
,
г) 
ВАРИАНТ 3
а) 
б) 
в) 
г) 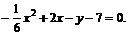
ВАРИАНТ 4
а) 
б) 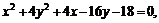
в) 
г) 
ВАРИАНТ 5
а) 
б)  ,
,
в) 
г) 
ВАРИАНТ 6
а) 
б) 
в) 
г) 
ВАРИАНТ 7
а) 
б) 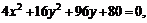
в)  ,
,
г) 
ВАРИАНТ 8
а) 
б) 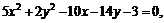
в) 
г) 
ВАРИАНТ 9
а) 
б) 
в) 
г) 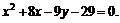
ВАРИАНТ 10
а) 
б) 
в) 
г) 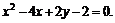
ЗАДАНИЕ 3
ВАРИАНТ 1
1. Найти величины отрезков, отсекаемых на осях координат плоскостью, проходящей через точку  параллельно плоскости
параллельно плоскости  .
.
2. Доказать параллельность прямых

ВАРИАНТ 2
1. Составить уравнение плоскости, проходящей через середину отрезка АВ перпендикулярно к этому отрезку, если  ,
,  .
.
2. Доказать, что прямая  параллельна плоскости
параллельна плоскости  , а прямая
, а прямая  лежит в этой плоскости.
лежит в этой плоскости.
ВАРИАНТ 3
1. Найти расстояние от точки  до плоскости
до плоскости  .
.
2. Составить уравнение прямой, проходящей через точку  и образующей с осями координат углы, соответственно равные
и образующей с осями координат углы, соответственно равные  .
.
ВАРИАНТ 4
1. Составить уравнение плоскости, проходящей через точку  параллельно плоскости
параллельно плоскости  .
.
2. Доказать, что прямая  перпендикулярна к прямой
перпендикулярна к прямой 
ВАРИАНТ 5
1. Составить уравнение плоскости, проходящей через ось  и точку
и точку  .
.
2. Составить параметрические уравнения медианы  треугольника с вершинами
треугольника с вершинами  ,
,  ,
,  .
.
ВАРИАНТ 6
1. Составить уравнение плоскости, проходящей через точки  ,
,  параллельно оси
параллельно оси  .
.
2. При каком значении  прямая
прямая  параллельна прямой
параллельна прямой 
ВАРИАНТ 7
1. Составить уравнение плоскости, проходящей через точку  и прямую
и прямую 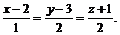
2. Найти точку пересечения прямой  и плоскости
и плоскости  .
.
ВАРИАНТ 8
1. Составить уравнение плоскости, проходящей через две параллельные прямые 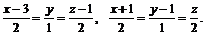
2. Найти проекцию точки  на плоскость
на плоскость  .
.
ВАРИАНТ 9
1. Составить уравнения прямой, образованной пересечением плоскости  с плоскостью, проходящей через ось
с плоскостью, проходящей через ось  и точку
и точку  .
.
2. При каком значении  плоскости
плоскости  и
и  перпендикулярны?
перпендикулярны?
ВАРИАНТ 10
1. Составить уравнение плоскости в отрезках, если она проходит через точку  и отсекает на оси
и отсекает на оси  отрезок
отрезок  , а на оси
, а на оси 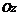 отрезок
отрезок 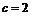 .
.
2. При каком значении 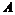 плоскость
плоскость  параллельна прямой
параллельна прямой 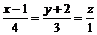 ?
?
ЗАДАНИЕ 4
ВАРИАНТ 1
Построить выпуклый многоугольник, заданный системой неравенств:

Пользуясь графическим методом, найти минимум и максимум линейной формы
L=2 x1+ x2-3
ВАРИАНТ 2
Построить выпуклый многоугольник, заданный системой неравенств:
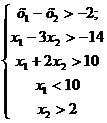
Пользуясь графическим методом, найти минимум и максимум линейной формы
L=2 x1+ x2-3
ВАРИАНТ 3
Построить выпуклый многоугольник, заданный системой неравенств:
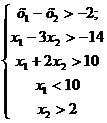
Пользуясь графическим методом, найти минимум и максимум линейной формы
L=2 x1+ x2-3
ВАРИАНТ 4
Построить выпуклый многоугольник, заданный системой неравенств:

Пользуясь графическим методом, найти минимум и максимум линейной формы
L=2 x1+ x2-3
ВАРИАНТ 5
Построить выпуклый многоугольник, заданный системой неравенств:

Пользуясь графическим методом, найти минимум и максимум линейной формы
L=2 x1+ x2-3
ВАРИАНТ 6
Построить выпуклый многоугольник, заданный системой неравенств:
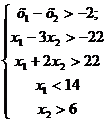
Пользуясь графическим методом, найти минимум и максимум линейной формы
L=2 x1+ x2-3
ВАРИАНТ 7
Построить выпуклый многоугольник, заданный системой неравенств:
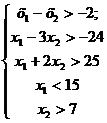
Пользуясь графическим методом, найти минимум и максимум линейной формы
L=2 x1+ x2-3
ВАРИАНТ 8
Построить выпуклый многоугольник, заданный системой неравенств:

Пользуясь графическим методом, найти минимум и максимум линейной формы
L=2 x1+ x2 - 3
ВАРИАНТ 9
Построить выпуклый многоугольник, заданный системой неравенств:

Пользуясь графическим методом, найти минимум и максимум линейной формы
L=2 x1+ x2-3
ВАРИАНТ 10
Построить выпуклый многоугольник, заданный системой неравенств:

Пользуясь графическим методом, найти минимум и максимум линейной формы
L=2 x1+ x2-3
ЗАДАНИЕ 5
Затраты четырех видов сырья (A, B, C, D), на производство единицы каждого из четырех видов продукции (1,2,3,4) и запасы каждого вида сырья задачи даны в таблице. Найти такой план выпуска продукции (план производства), при котором полностью используются запасы каждого вида сырья. При решении задачи требуется:
1. Составить экономико-математическую модель задачи;
2. Решить систему линейных уравнений методом полного исключения переменных;
3. Дать экономическую интерпретацию полученного плана производства.
| ВАРИАНТ | ВИД СЫРЬЯ | ЗАТРАТЫ СЫРЬЯ НА ЕДИНИЦУ ПРОДУКЦИИ | ЗАПАСЫ СЫРЬЯ | |||
| 1 | 2 | 3 | 4 | |||
| 1 | A | 3 | 2 | 7 | 4 | 95 |
| B | 4 | 3 | 5 | 2 | 75 | |
| C | 5 | 4 | 3 | 3 | 79 | |
| D | 2 | 1 | 5 | 3 | 67 | |
| 2 | A | 3 | 2 | 7 | 3 | 107 |
| B | 4 | 3 | 5 | 1 | 84 | |
| C | 5 | 4 | 3 | 1 | 81 | |
| D | 2 | 6 | 5 | 1 | 87 | |
| 3 | A | 2 | 2 | 7 | 8 | 144 |
| B | 3 | 3 | 5 | 2 | 83 | |
| C | 7 | 4 | 3 | 2 | 94 | |
| D | 12 | 1 | 5 | 3 | 115 | |
| 4 | A | 3 | 4 | 7 | 5 | 127 |
| B | 4 | 5 | 5 | 7 | 133 | |
| C | 5 | 2 | 3 | 9 | 103 | |
| D | 2 | 6 | 5 | 11 | 148 | |
| 5 | A | 3 | 4 | 10 | 5 | 104 |
| B | 4 | 5 | 6 | 7 | 102 | |
| C | 5 | 2 | 4 | 9 | 94 | |
| D | 2 | 6 | 3 | 11 | 95 | |
| 6 | A | 3 | 4 | 1 | 5 | 67 |
| B | 4 | 5 | 5 | 7 | 134 | |
| C | 5 | 2 | 4 | 9 | 125 | |
| D | 2 | 6 | 3 | 5 | 96 | |
| 7 | A | 3 | 4 | 1 | 2 | 61 |
| B | 3 | 5 | 5 | 4 | 89 | |
| C | 5 | 2 | 4 | 8 | 97 | |
| D | 2 | 6 | 3 | 7 | 106 | |
| 8 | A | 0 | 4 | 11 | 2 | 127 |
| B | 7 | 3 | 5 | 4 | 127 | |
| C | 5 | 2 | 4 | 13 | 143 | |
| D | 2 | 6 | 3 | 7 | 128 | |
| 9 | A | 5 | 4 | 11 | 2 | 133 |
| B | 7 | 0 | 5 | 4 | 89 | |
| C | 5 | 8 | 4 | 13 | 137 | |
| D | 2 | 6 | 10 | 7 | 133 | |
| 10 | A | 3 | 12 | 7 | 11 | 86 |
| B | 4 | 3 | 5 | 2 | 46 | |
| C | 5 | 4 | 3 | 3 | 46 | |
| D | 2 | 1 | 0 | 3 | 16 | |
ЛИТЕРАТУРА:
| Основная: | |
| 1 | Общий курс высшей математики для экономистов : учебник / Под ред. В. И. Ермакова. - М. : ИНФРА-М, 2007. - 656 с. - Г / МО. |
| 2 | Сборник задач по высшей математике для экономистов : учеб. пособие / Под ред. В. И. Ермакова. - 2-е изд., испр. - М. : ИНФРА-М, 2008. - 575 с. - (100 лет РЭА им. Г. В. Плеханова). - Г / УМО. |
| Дополнительная: | |
| 1 | Алескеров, Ф. Т. Бинарные отношения, графы и коллективные решения : учеб. пособие / Ф. Т. Алескеров, Э. Л. Хабина, Д. А. Шварц. - М. : Издательский дом ГУ ВШЭ, 2006. - 298 с. - (Учебники Высшей школы экономики). - Г / МО. |
| 2 | Баврин, И. И. Высшая математика : учебник / И. И. Баврин, В. Л. Матросов. - М. : Гуманит. изд.центр ВЛАДОС, 2003. - 400 с. - (Учебник для вузов). - Г / МО. |
| 3 | Высшая математика для экономистов : курс лекций / Под ред. П. С. Геворкяна. - М. : Экономика, 2010. - 351 с. - (Высшее образование). - Г / МО. |
| 4 | Высшая математика для экономистов : учебник / Под ред. Н. Ш. Кремера. - 3-е изд. - М. : ЮНИТИ-ДАНА, 2008. - 479 с. - (Золотой фонд российских учебников). - Г / МО. |
| 5 | Высшая математика для экономистов : учебник / Под ред. проф. Н. Ш. Кремера. - 3-е изд. - М. : ЮНИТИ, 2007. - 479 с. - (Золотой фонд российских учебников). - Г / МО. |
| 6 | Высшая математика для экономических специальностей : учебник и практикум / Под ред. Н. Ш. Кремера. - 3-е изд., перераб. и доп. - М. : Юрайт, Высшее образование, 2010. - 909 с. - (Основы наук). - Г / МО. |
| 7 | Кремер, Н. Ш. Математика для экономистов: от Арифметики до Эконометрики : учеб. пособие / Н. Ш. Кремер, Б. А. Путко, И. М. Тришин ; Под ред. Н. Ш. Кремера. - 2-е изд., перераб. и доп. - М. : Юрайт; ИД Юрайт, 2011. - 646 с. - (Основы наук). - Г / УМО. |
| 8 | Письменный, Д. Т. Конспект лекций по высшей математике : тридцать шесть лекций. Ч. 1 / Д. Т. Письменный. - 3-е изд. - М. : Айрис - пресс, 2004. - 288 с. |
| 9 | Письменный, Д. Т. Конспект лекций по высшей математике: полный курс : курс лекций / Д. Т. Письменный. - 9-е изд. - М. : Айрис-пресс, 2009. - 608 с. - (Высшее образование). |
Программное обеспечение:
1.Макаров, С. И. Математика для экономистов : электронный учебник / С. И. Макаров. - М. : КНОРУС, 2009. - 1 электрон. опт. диск. - Г / УМО.
2. Макаров, С. И. Математика для экономистов : электронный учебник / С. И. Макаров. - М. : КНОРУС, 2010. - 1 электрон. опт. диск. - Г / УМО.
3. Электронная библиотечная система «Ай Пи Ар Букс» - электронная библиотека
полнотекстовых изданий.
Информационно-справочная и поисковая система:
1. Справочник по математике для экономистов : учеб. пособие / Под ред. В. И. Ермакова. - 3-е изд., перераб. и доп. - М. : ИНФРА-М, 2007. - 464 с. - (100 лет РЭА им.Г.В. Плеханова). - Г / УМО.
Дата добавления: 2018-02-15; просмотров: 677; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
