Подходящие дроби и их свойства
 - конечная цепная дробь.
- конечная цепная дробь.
Определение. Подходящей дробью k – го порядка к конечной цепной дроби называется дробь, которая остается после отбрасывания элементов, начиная с 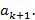
Обозначается 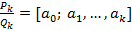 .
.
Из определения следует, что всякая конечная цепная дробь равна своей последней подходящей дроби,  .
.
Свойства подходящих дробей:
1) 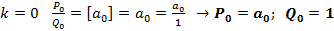 ;
;

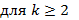
 ;
;


2) При  справедливо равенство
справедливо равенство 
3) Подходящие дроби несократимы, т.е. ( 
4) Знаменатели подходящих дробей, начиная с 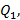 образуют возрастающую последовательность.
образуют возрастающую последовательность.
5) Для  справедливо равенство
справедливо равенство 
6) Для  справедливо равенство
справедливо равенство 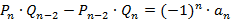
7) Подходящие дроби с четными индексами образуют возрастающую последовательность, а с нечетными – убывающую
8) Всякая четная подходящая дробь меньше любой нечетной подходящей дроби.
Замечание. Из свойства 3 следует, что если дробь  разложить в конечную цепную дробь, то ее последняя подходящая дробь будет несократимой и равной
разложить в конечную цепную дробь, то ее последняя подходящая дробь будет несократимой и равной  .
.
Пример. Сократите дробь, разлагая ее в конечную цепную дробь  .
.
Решение.
С помощью алгоритма Евклида разложим дробь в конечную цепную дробь:
1043=3427 
3427=1043  3+298
3+298
104298  3+149
3+149
298=149  2
2

Подходящие дроби удобно вычислять по следующей схеме с помощью таблицы:
| k | 0 | 1 | 2 | 3 |

| 0 | 3 | 3 | 2 |
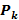
| 
| 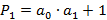 =0 =0  3+1=1 3+1=1
| 
| 
|
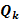
| 
| 
|   =10 =10
|  
|
Таким образом, 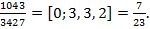
Неопределенные уравнение первой степени с двумя неизвестными
|
|
|
Определение . Алгебраические уравнения или системы алгебраических уравнений с целыми коэффициентами, решения которых отыскиваются в целых или рациональных числах, называются диофантовыми (неопределенными).
Рассмотрим линейное уравнение  (1), где
(1), где 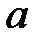 ,
,  - ненулевые целые числа, с – любое целое число.
- ненулевые целые числа, с – любое целое число.
Определение. Решением уравнения (1) называется упорядоченная пара целых чисел, удовлетворяющая уравнению.
Теорема 1. Если в уравнении ах+ by = c , ( a , b )= d >1 и c не  d , то уравнение (1) не имеет решений.
d , то уравнение (1) не имеет решений.
Теорема 2. Если в уравнении ах+ by = c , ( a , b )= d >1 и c  d , то оно равносильно уравнению a 1 х+ b 1 y = c 1 , в котором ( a 1 , b 1 )=1.
d , то оно равносильно уравнению a 1 х+ b 1 y = c 1 , в котором ( a 1 , b 1 )=1.
Рассмотрим уравнение ах+ by = c , ( a , b )=1. (1)
Пусть  и
и  удовлетворяют уравнению (1), т.е. а
удовлетворяют уравнению (1), т.е. а  + b
+ b  = c верное равенство. Тогда
= c верное равенство. Тогда  ,
, 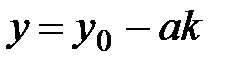 с целым параметром
с целым параметром  задают все решения уравнения. Основной проблемой решения уравнения (1) является нахождение частного решения (
задают все решения уравнения. Основной проблемой решения уравнения (1) является нахождение частного решения (  ,
,  ).
).
Разложим отношение коэффициентов 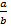 в конечную цепную дробь и найдем ее подходящие дроби
в конечную цепную дробь и найдем ее подходящие дроби  =
= 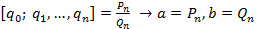 .
.
По свойству подходящих дробей

 .
.
Следовательно,  =
= 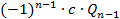 ,
,  =
= 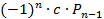 .
.
Таким образом, общее решение уравнения (1) находится по формулам
|
|
|

 .
.
Пример. Решить уравнение в целых числах  .
.
Решение.
(31, 42)=1, значит уравнение имеет бесконечное множество целочисленных решений. Разложим в непрерывную дробь отношение коэффициентов 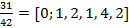 и найдем подходящие дроби
и найдем подходящие дроби
| k | 0 | 1 | 2 | 3 | 4 | 5 |

| 0 | 1 | 2 | 1 | 4 | 2 |

| 0 | 1 | 2 | 3 | 14 | 31 |

| 1 | 1 | 3 | 4 | 19 | 42 |

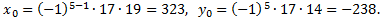
Ответ. x 
y  .
.
Пример. Решить уравнение в целых числах  .
.
Решение.
Перепишем уравнение в виде  и решим это уравнение относительно неизвестных x и - y.
и решим это уравнение относительно неизвестных x и - y.
(10, 17)=1, значит уравнение имеет бесконечное множество целочисленных решений. Разложим в непрерывную дробь отношение коэффициентов 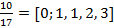 и найдем подходящие дроби
и найдем подходящие дроби
| k | 0 | 1 | 2 | 3 | 4 |

| 0 | 1 | 1 | 2 | 3 |

| 0 | 1 | 1 | 3 | 10 |

| 1 | 1 | 2 | 5 | 17 |


x 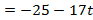
 y
y  .
.
Ответ. x 
y  .
.
Дата добавления: 2021-05-18; просмотров: 286; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
