Наибольший общий делитель нескольких чисел
Лекция 1
Теория чисел – раздел математики, посвященный изучению свойств целых, рациональных и алгебраических чисел. Теория чисел изучает также и свойства произвольных чисел, вытекающие из возможности приближения этих чисел рациональными. Целое число, наряду с простейшими геометрическими фигурами, является первым и древнейшим математическим понятием.
В теории чисел, естественно, выделяются и рассматриваются в первую очередь те проблемы, которые глубоко и достаточно непосредственно связаны с изучаемыми объектами и важны для построения математики в ее целом. Некоторые теоретико-числовые задачи возникают уже в рамках школьного курса арифметики. Исторически теория чисел возникла как непосредственное развитие арифметики. В настоящее время в теорию чисел включают значительно более широкий круг вопросов, выходящих за рамки изучения натуральных чисел. В теории чисел рассматриваются не только натуральные числа, но и множество всех целых чисел, а также множество рациональных чисел.
В теорию чисел включают также вопросы, связанные с приближением действительных чисел рациональными дробями. Такие приближения называют, обычно, диофантовыми приближениями, по имени великого греческого математика Диофанта.
Для современной теории чисел характерно применение весьма разнообразных методов исследований; так, например, многие проблемы теории чисел могут быть, естественно, сформулированы в геометрической форме, и к решению такого рода задач применяют геометрические соображения (геометрическая теория чисел). В современной теории чисел широко пользуются методами математического анализа; в частности, при изучении вопросов, связанных с распределением простых чисел, особенно часто приходится применять теорию функций комплексного переменного.
|
|
|
Развитие теории чисел тесно и непосредственно связано с развитием целого ряда разделов математики.
Теория чисел не только широко использует методы, разработанные в смежных математических дисциплинах, но и сама влияет на формирование этих дисциплин. Так, например, начало глубоких исследований в теории алгебраических чисел было связано с так называемой проблемой Ферма о возможности существования целых положительных решений неопределенного уравнения 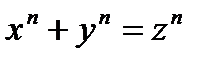 при
при 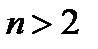 ; дальнейшее развитие этой теории оказало решающее влияние на современную алгебру, а возникшие в теории чисел понятия «кольца», «идеала» являются одними из основных понятий всей математики нашего времени. Ряд вопросов теории чисел находит себе применение на практике, например, в теории телефонных сетей (кабелей), в кристаллографии, при решении некоторых задач теории приближенных вычислений.
; дальнейшее развитие этой теории оказало решающее влияние на современную алгебру, а возникшие в теории чисел понятия «кольца», «идеала» являются одними из основных понятий всей математики нашего времени. Ряд вопросов теории чисел находит себе применение на практике, например, в теории телефонных сетей (кабелей), в кристаллографии, при решении некоторых задач теории приближенных вычислений.
|
|
|
Дисциплина «Теория чисел» состоит из двух разделов:
1. Теория делимости в кольце целых чисел;
2. Числовые сравнения. Сравнения с неизвестной величиной.
Форма отчетности – экзамен.
В рамках дисциплины используется балльно-рейтинговая система оценивания индивидуальных результатов обучения.
Деление в кольце целых чисел
Определение. Говорят, что целое число а делится на целое число b ¹ 0, если существует целое число с такое, что а = b × с
Свойства делимости:
1. " а 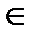 Z, а ¹ 0 а ∶ а (свойство рефлексивности)
Z, а ¹ 0 а ∶ а (свойство рефлексивности)
2. " а 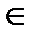 Z, а ∶ 1
Z, а ∶ 1
3. Если а ∶ b, то при любой комбинации знаков ( ± а) ∶ ( ± b)
3. а ∶ b ۸ b ∶ с Þ а ∶ с (свойство транзитивности)
4. а ∶ b ۸ b ∶ а Þ а = 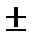 b
b
5. а ∶ с ۸ b ∶ с Þ (а + b) ∶ с ۸ (а - b) ∶ с
6. (а + b) ∶ с ۸ а ∶ с Þ b ∶ с
7. а ∶ b , с Î Z Þ (а · с) ∶ b
8. а 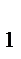 ∶ b , а
∶ b , а  ∶ b, …, а k ∶ b, с
∶ b, …, а k ∶ b, с 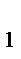 , с
, с 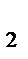 , …, с k Î Z Þ (а
, …, с k Î Z Þ (а 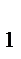 с
с 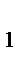 + а
+ а 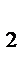 с
с 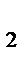 + …+ а k с k ) ∶ b
+ …+ а k с k ) ∶ b
9. (а · b) ∶ с ۸ (b, с) = 1 Þ а ∶ с
10. а ∶ b Þ 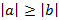
Замечание. В силу свойства 2 делитель можно считать натуральным числом.
Деление с остатком
Определение. Говорят, что число а Î Z при делении на целое число b ≠ 0 дает частное q и остаток r, если а = b · q + r
|
|
|
Например: 19=5·3+4; 49=7·7+0
Теорема (о существовании и единственности частного и остатка.)
Для любого целого числа а и целого числа b ≠ 0 найдется и притом единственная пара целых чисел q и r, удовлетворяющая условию а = b · q + r, где 0 £ r< ½b½
Доказательство: (Доказательство проведем для случая а Î Z и b Î N.)
Доказательство существования.
1. а ∶ b Þ $ q Î Z : а = b · q = b · q + 0, 0 £ 0 < b.
2. а не делится на b. Рассмотрим кратные числа b:
… -2·b, - 1·b, 0·b, b·1, b·2, b·3,…,b·к,…
Если а > 0, то найдется целое число q такое, что b · q < а < b · (q+1) Þ
0 < (а – b) · q < b. Обозначим (а – b) · q) = r. Тогда а = b · q + r, 0 < r < b.
Если а < 0, то найдутся целые числа q 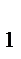 и r
и r 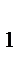 такие, что – а = b · q
такие, что – а = b · q 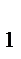 + r
+ r 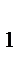 , 0 < r
, 0 < r 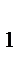 < b
< b
a = b (-q1) - r1= b (-q 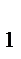 ) - b + b - r
) - b + b - r 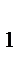 = b (-q
= b (-q 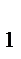 - 1) + (b – r
- 1) + (b – r 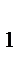 )
)
Обозначим – q 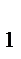 -1= q, b - r
-1= q, b - r 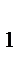 = r, тогда получим
= r, тогда получим
a = b·q+r, 0 < r < b, т.к. 0 < r 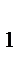 < b Þ 0 > - r
< b Þ 0 > - r 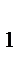 > -b Þ 0 < b- r
> -b Þ 0 < b- r 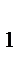 < b.
< b.
Доказательство единственности.
Предположим, что существуют две пары чисел q, r и q 1 , r 1, удовлетворяющие условию теоремы, т.е. а = b· q + r, 0 ≤ r < b и а = b ·q 1 + r 1 , 0 ≤ r 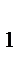 < b.
< b.
Тогда b + r = b·q 1 + rÞ b·(q-q 1 ) = r1 - r .
1. Если q = q 1, то q 1 -q = 0 Þ r 1 -r = 0 Þ r 1 -r=0 Þ r 1 = r
2. Если q ¹ q 1, то r1-r ¹ 0 и (r1 - r) ∶ b.
|
|
|
Но ½ r 1 -r ½ < b и ½ r 1 -r ½ ∶ b Þ ½ r 1 - r ½ = 0 Þ r 1 -r=0. Что противоречит r 1 -r ¹ 0.
Значит, наше предположение не верно и пара чисел q и r является единственной.
Теорема о существовании и единственности частного и остатка является теоретической основой метода остатков При решении задач методом остатков используются свойства делимости целых чисел.
Теорема о делении с остатком позволяет разбить бесконечное множество целых чисел Z на конечное число классов равноостаточных чисел. Множество Z-счетное, его элементы нельзя перебрать непосредственно, но их можно распределить по конечному числу классов и перебрать по классам, используя общий вид представителей данного класса
| 0 | 1 | 2 | … | m-1 |
| b · q | bq +1 | bq +2 | … | bq +(m-1) |
Задача.
Доказать, что произведение 3-х последовательных целых чисел делится
на 3.
Решение.
Пусть а Î Z. Доказать, что а(а+1)(а+2) ∶ 3
По теореме о делении с остатком для любых целых чисел а и 3 найдутся числа q и r такие, что а = 3 q + r, где 0 £ r < 3
r = 0 Þ а = 3 qÞ а(а+1) (а+2) = 3 q (3 q +1) (3 q +2) ∶ 3
r = 1Þ а = 3 q +1Þ а(а+1)(а+2)=(3 q +1)(3 q +2)3( q +1) ∶ 3
r = 2 Þ а = 3 q +2Þ а(а+1)(а+2)=(3 q +2)3( q +1)(3 q +4) ∶ 3
Значит, для " а Î Z а(а+1)(а+2) ∶ 3.
Замечание: аналогично можно доказать, что произведение n последовательных целых чисел делится на n.
Наибольший общий делитель нескольких чисел
Определение. Число D называется общим делителем чисел 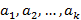 , если каждое из этих чисел делится на D.
, если каждое из этих чисел делится на D.
Определение. Наибольшим общим делителем чисел 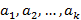 называется такой их общий делитель, который делится на любой общий делитель этих чисел.
называется такой их общий делитель, который делится на любой общий делитель этих чисел.
Обозначается: 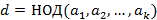 или
или 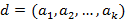 .
.
Теорема. НОД( 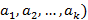 определяется однозначно с точностью до знака.
определяется однозначно с точностью до знака.
Поэтому будем считать, что 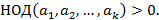
Алгоритм Евклида
Теорема 1. Если 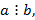 то НОД(a , b )= b .
то НОД(a , b )= b .
Теорема 2. Если 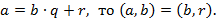
Таким образом, наибольший общий делитель двух чисел равен последнему отличному от 0 остатку в алгоритме Евклида.
Пример.
Пусть 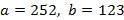 . Запишем деление уголком, и каждый раз то, что было в уголке, т.е. делитель приписывается к остатку от деления с левой стороны, а остаток, как новый делитель, берется в уголок.
. Запишем деление уголком, и каждый раз то, что было в уголке, т.е. делитель приписывается к остатку от деления с левой стороны, а остаток, как новый делитель, берется в уголок.
252|123
246|2
123|6
12 |20
6| 3
6|2
0
Запись того же самого процесса деления в виде цепочки равенств:
252=123∙2+6
123=6∙20+3
6=3∙2
Таким образом, (252, 123)=3.
Свойства НОД
1) 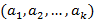
 .
.
2) Наибольший из общих делителей чисел 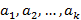 является их НОД.
является их НОД.
3) 
4) НОД двух чисел линейно выражается через эти числа, т.е.
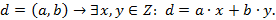
Взаимно простые числа
Определение. Числа 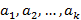 называются взаимно простыми, если их НОД равен 1.
называются взаимно простыми, если их НОД равен 1.
Определение. Числа 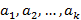 называются попарно взаимно простыми, если при любых
называются попарно взаимно простыми, если при любых
 .
.
Свойства взаимно простых чисел
1) Характеристическое свойство: 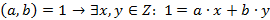
2) 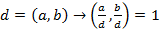
3) 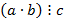 и (a, c)=1
и (a, c)=1 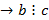
4) 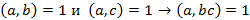
5) Если а ∶ b 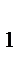 , а ∶ b
, а ∶ b 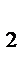 , …, а ∶ b k и числа b
, …, а ∶ b k и числа b 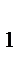 , b
, b 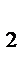 , …b k попарно взаимно простые, то а ∶ (b
, …b k попарно взаимно простые, то а ∶ (b 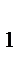 · b
· b  · … · b k )
· … · b k )
Дата добавления: 2021-05-18; просмотров: 154; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
