Наименьшее общее кратное чисел
Пусть 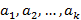 - целые числа, отличные от 0.
- целые числа, отличные от 0.
Определение. Число М называется общим кратным чисел 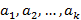 , если оно делится на каждое из этих чисел.
, если оно делится на каждое из этих чисел.
Определение. Наименьшим общим кратным чисел 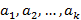 называется такое их положительно общее кратное, на которое делится любое общее кратное этих чисел.
называется такое их положительно общее кратное, на которое делится любое общее кратное этих чисел.
Обозначается:  или
или 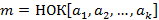 .
.
Свойства наименьшего общего кратного
1) Произведение НОД двух чисел на их НОК равно произведению этих чисел, т.е. 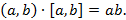
2) 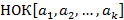 есть наименьшее из положительных общих кратных этих чисел
есть наименьшее из положительных общих кратных этих чисел
3) 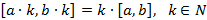
4) 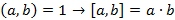 .
.
Простые и составные числа
Определение. Число  ,
, 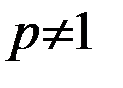 , называется простым, если
, называется простым, если 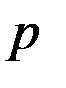 имеет
имеет
только два натуральных делителя: 1 и 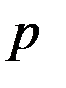 .
.
Пример: 2, 3, 5, 7, 11, 13, 17, …
Определение. Число  ,
, 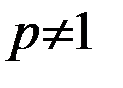 , называется составным, если оно имеет больше двух натуральных делителей.
, называется составным, если оно имеет больше двух натуральных делителей.
Пример: 4, 6, 8, 9, 10, 12, 14, 16, …
Число 1 – ни простое, ни составное.
Свойства простых и составных чисел
1) Наименьший положительный делитель натурального числа n>1 есть простое число
2) Если  .
.
3) Если 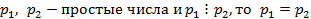 .
.
4) Если произведение нескольких чисел делится на простое число, то хотя бы один из множителей делится на это простое число
5) Если натуральное число n>1 не делится ни на одно простое число, не превосходящее 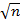 , то оно простое (критерий простого числа)
, то оно простое (критерий простого числа)
6) Множество простых чисел бесконечно.
7) Для составления простых чисел Эратосфен придумал процедуру, которая получила название «решето Эратосфена»:
|
|
|
2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,…
Идем по натуральному ряду слева направо. Обводим первое число, а из дальнейшего ряда вычеркиваем числа, кратные ему. Процедуру повторяем многократно. Оставшиеся не вычеркнутыми числа – простые.
Основная теорема арифметики: каждое натуральное число, отличное от 1 либо является простым, либо представимо в виде произведения простых чисел и такое представление единственно с точностью до порядка следования множителей.
(доказать существование можно методом спуска или методом математической индукции; доказательство единственности – методом от противного).
Следствия:
1.Всякое натуральное число n однозначно представимо в виде
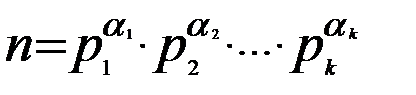 , где
, где 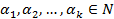 .
.
Определение. Каноническим разложением натурального числа n > 1 называется его представление в виде произведения степеней различных простых чисел.
2. Если 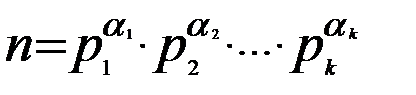 и
и 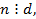 то
то 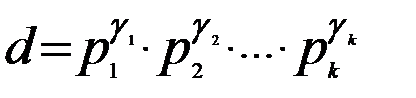 , где
, где 
3. Если 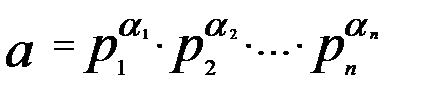 ,
,  - натуральные числа, то наибольший общий делитель a и b равен
- натуральные числа, то наибольший общий делитель a и b равен 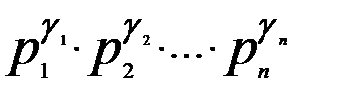 , а наименьшее общее кратное a и b равно
, а наименьшее общее кратное a и b равно  , где
, где 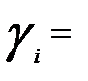 min{
min{  ,
,  },
}, 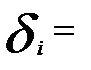 max{
max{ 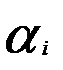 ,
,  }.
}.
Арифметические функции: целая и дробная часть числа
Определение. Пусть 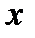 - действительное число. Целой частью
- действительное число. Целой частью 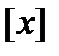
числа 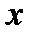 называется наибольшее целое число, не превосходящее
называется наибольшее целое число, не превосходящее 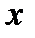 ; дробной частью {
; дробной частью { 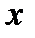 } числа
} числа 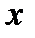 называется число {
называется число { 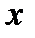 }=
}= 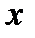 - [
- [ 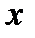 ].
].
|
|
|
Например, [2,25]=2; {2,25}=0,25; [-0,3]=-1; {-0,3}=0,7.
Целая часть – неубывающая функция, дробная часть – периодическая функция с периодом 1; дробная часть всегда неотрицательна, но меньше единицы; обе эти функции разрывны при целых значениях 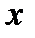 , но непрерывны при этих
, но непрерывны при этих 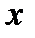 справа.
справа.
Теорема. Показатель, с которым простое число 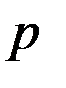 входит в разложение
входит в разложение 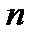 !,
!,
равен 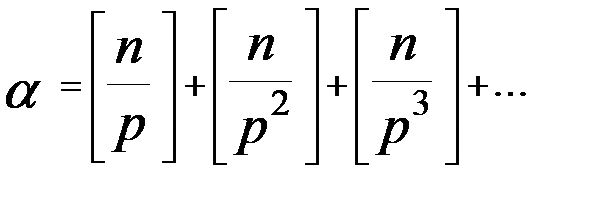

Ряд обрывается на том месте 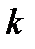 , на котором
, на котором 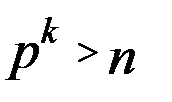 .
.
Например, показатель, с которым 5 входит в разложение 126! равен 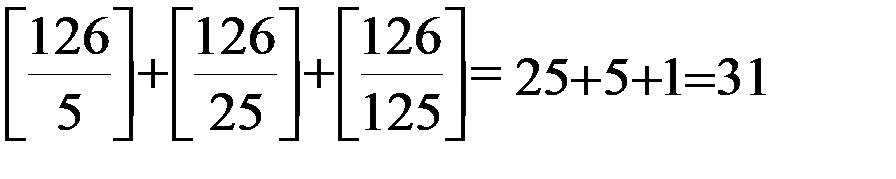
В теории чисел рассматриваются разнообразные функции, значения которых при натуральных значениях аргумента n связаны c арифметической природой числа n. Множество рассматриваемых функций не ограничивают какими-либо требованиями, кроме того, чтобы каждая функция была определена для всех натуральных значений аргумента. Такие функции называют числовыми функциями. Рассмотрим числовые функции  , зависящие от делителей аргумента.
, зависящие от делителей аргумента. 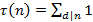 определяется как число натуральных делителей натурального числа n,
определяется как число натуральных делителей натурального числа n, 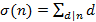 определяется как сумма натуральных делителей натурального числа n. Например,
определяется как сумма натуральных делителей натурального числа n. Например,  , так как 6 делится на 1, 2, 3, 6.
, так как 6 делится на 1, 2, 3, 6.
Свойства функций 
1) 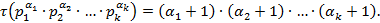
2)  .
.
3) Функции  - мультипликативны, т.е. если
- мультипликативны, т.е. если 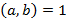 , то
, то  =
= 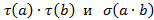 =
= 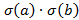 .
.
|
|
|
Конечные цепные дроби
Определение. Конечной цепной ( непрерывной) дробью называется число, записанное в виде:
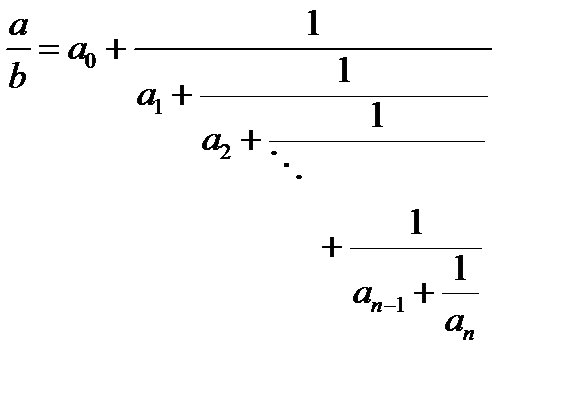 где
где 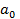 – целое число,
– целое число, 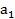 ,
, 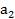 , …,
, …, 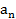 - натуральные числа, неполные частные и
- натуральные числа, неполные частные и 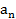 ≠1,
≠1, 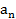 >1.
>1.
Числа 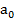 ,
, 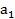 , …,
, …, 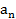 называют элементами цепной дроби.
называют элементами цепной дроби.
Условимся в целях технического удобства писать в дальнейшем конечную цепную дробь в виде [a 0; a 1, a 2, …, an] .
Цепная дробь может быть как конечной (содержащей конечное число дробных линий и неполных частных), так и бесконечной вниз и вправо. В первом случае –это некоторое рациональное число.
Теорема. Любое рациональное число может быть представлено в виде конечной цепной дроби.
Доказательство.
Любое рациональное число можно представить в виде  , где a и b целые, причем b≥l. Алгоритм Евклида для таких чисел a и b дает цепь равенств:
, где a и b целые, причем b≥l. Алгоритм Евклида для таких чисел a и b дает цепь равенств:
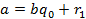
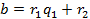
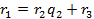 (1)
(1)
……………….
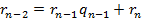
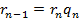
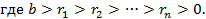
Равенства (1) можно записать в следующем виде:
Последовательность равенств (1) можно записать в виде равносильной цепочки
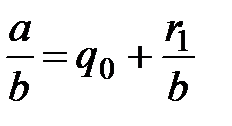 ,
, 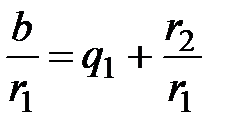 ,
, 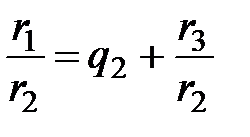 , …
, …
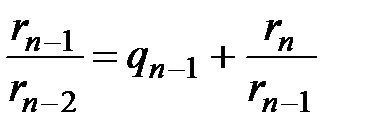 ,
,  . (2)
. (2)
Выразим отношение 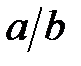 через одни только числа
через одни только числа 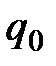 ,
, 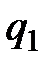 , …,
, …,  ,
, 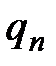 . На основании равенств (2) находим:
. На основании равенств (2) находим:
|
|
|
 (3)
(3)
В этом равенстве 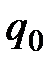 - целое число,
- целое число, 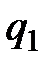 ,
, 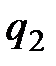 , …,
, …, 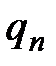 - целые положительные числа.
- целые положительные числа.
Итак,  – элементами конечной цепной дроби являются неполные частные в алгоритме Евклида, записанные в том порядке, в котором они получены.
– элементами конечной цепной дроби являются неполные частные в алгоритме Евклида, записанные в том порядке, в котором они получены.
Пример 1. Разложить дробь в непрерывную 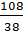 .
.
Используем алгоритм Евклида:
105 = 38 · 2 + 29,
38 = 29 · 1 + 9,
29 = 9 · 3 + 2,
9 = 2 · 4 + 1,
2 = 1 · 2.
Неполные частные специально подчеркнуты потому, что теперь для написания ответа нужно аккуратно расположить их подряд на этажах цепной дроби перед знаками плюс:
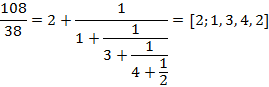
Получили представление данной дроби в виде непрерывной цепной дроби.
Пример 2. Разложить в непрерывную дробь 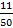 .
.
Аналогично предыдущему примеру:
11 = 50 · 0 +11,
50 = 11 · 4 + 6,
11 = 6 · 1 + 5,
6 = 5 · 1 + 1,
5 = 1 · 5.
Получили: 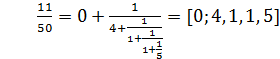
Алгоритм Евклида дает возможность найти представление любого рационального числа в виде цепной дроби. В качестве элементов цепной дроби берутся неполные частные последовательных делений, поэтому элементы цепной дроби называются также неполными частными.
Разложение рационального числа имеет, очевидно, конечное число элементов, так как алгоритм Евклида является конечным.
Дата добавления: 2021-05-18; просмотров: 51; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
