МЭ олимпиады. 2016 год. Решения. 10 Класс
1. Обозначим число 2015 за a . Тогда 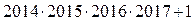 =
=
= (a – 1)a(a + 1)(a + 2) + 1 =  =
= 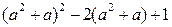 = =
= = 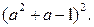
Поэтому, 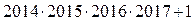 =
= 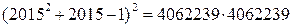 .
.
2. Заметим, что все члены последовательности, начиная с sin 1000º, равны между собой, так как разность между числами 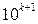 и
и 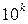 при натуральных k > 2 кратна 360. Действительно
при натуральных k > 2 кратна 360. Действительно 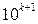 -
- 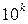 =
= 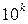 (10 – 1) = 9∙
(10 – 1) = 9∙ 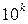 =
= 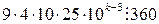 . Непосредственной проверкой убеждаемся, что sin 1º > 0, sin 10º > 0, sin 100º > 0, sin 1000º = sin (360º∙3 - 80º) = sin (-80º) < 0. Значит, и остальные члены последовательности будут отрицательные. Таким образом, положительных членов среди первых 100 членов последовательности будет ровно три.
. Непосредственной проверкой убеждаемся, что sin 1º > 0, sin 10º > 0, sin 100º > 0, sin 1000º = sin (360º∙3 - 80º) = sin (-80º) < 0. Значит, и остальные члены последовательности будут отрицательные. Таким образом, положительных членов среди первых 100 членов последовательности будет ровно три.
Ответ:3.
3. Так как M и K являются серединами сторон, то продолжим отрезки NM и NK за указанные точки на такое же расстояние и соединим точки L , B , A , N; а также F , B , N , C . Тогда четырехугольники ALBN , NBFC являются параллелограммами. Так как в параллелограмме сумма квадратов диагоналей равна сумме квадратов его сторон, то имеем:
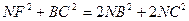 (для параллелограмма NBFC) и
(для параллелограмма NBFC) и
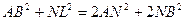 (для параллелограмма ALBN).
(для параллелограмма ALBN).
Выразим из первого равенства 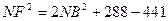 и, учитывая, что MN = KN , получим:
и, учитывая, что MN = KN , получим: 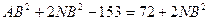 , откуда AB = 15 см.
, откуда AB = 15 см.

Ответ:15 см.
4. Первый способ. Рассмотрим различные случаи:
1) Если x  0, то левая часть уравнения будет положительная, поэтому уравнение не имеет корней.
0, то левая часть уравнения будет положительная, поэтому уравнение не имеет корней.
2) Преобразуем уравнение 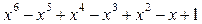 = 0 к виду:
= 0 к виду:  . Данное уравнение не имеет решений при 0 < x < 1.
. Данное уравнение не имеет решений при 0 < x < 1.
3) Преобразуем уравнение 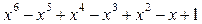 = 0 к виду:
= 0 к виду: 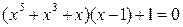 . Данное уравнение не имеет решений при x
. Данное уравнение не имеет решений при x 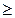 1.
1.
Таким образом, ни при каком действительном x данное уравнение не имеет решений.
|
|
|
Второй способ. Домножим обе части уравнений 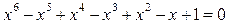 на x + 1. Тогда получим уравнение
на x + 1. Тогда получим уравнение 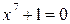 , которое имеет корень x = - 1. Но проверкой убеждаемся, что число x = - 1 не является корнем исходного уравнения.
, которое имеет корень x = - 1. Но проверкой убеждаемся, что число x = - 1 не является корнем исходного уравнения.
5. Заметим, что нечетное полупростое число может быть лишь суммой двойки и нечетного простого числа.
Покажем, что три подряд идущих нечетных числа 2n + 1, 2n + 3, 2n + 5, больших 25, не могут быть полупростыми одновременно. Предположим противное. Тогда получим, что числа 2n – 1, 2n + 1, 2n + 3 – простые, и все они больше 3. Но одно из этих трех чисел делится на 3. Получаем противоречие. Поэтому три подряд идущих нечетных числа 2n + 1, 2n + 3, 2n + 5, больших 25, не могут быть полупростыми одновременно.
Заметим, что среди любых шести последовательных натуральных чисел есть три подряд идущих нечетных числа, значит, последовательных полупростых чисел не может быть больше пяти. Пять подряд идущих чисел могут быть полупростыми; например, 30 = 17 +13, 31 = 29 + 2, 32 = 19 + 13, 33 = 31 + 2, 34 = 23 + 11. Существуют и другие примеры.
Ответ: 5.
ШЭ олимпиады. Решение.10 класс. 2017г.
1.Пусть x- первоначальное число учащихся в лицее, тогда мальчиков из них было 0,5x. После указанных событий учащихся стало 0,9x, а мальчиков 0,9x· 0,55=0,495x. Так как 0,495x< 0,5x, то мальчиков стало меньше.
|
|
|
Ответ. Количество мальчиков уменьшилось.
2. Если x – число лошадей, y – число быков, то 31x+ 21y = 1770.
Из уравнения получаем 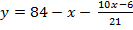 . Выражение
. Выражение 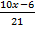 должно быть целым числом, оканчивающимся на 4. Таких чисел, удовлетворяющих условию задачи, всего три: 4, 14, 24. Далее находим x и y.
должно быть целым числом, оканчивающимся на 4. Таких чисел, удовлетворяющих условию задачи, всего три: 4, 14, 24. Далее находим x и y.
Ответ. 9 лошадей, 71 бык; 30 лошадей, 40 быков; 51 лошадь, 9 быков.
3. Решение. 1. D=22- 4а*1=4-4а
2. По теореме Виета х1+х2 =  ; х1х2 =
; х1х2 = 
3. (х1-х2)2 = х12-2х1х2 + х22=(х12+2х1х2 + х22)-4х1х2=(х1+х2)2-4х1х2=
= 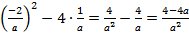
4. Дискриминант уравнения в 9 раз больше квадрата разности двух его различных корней, тогда

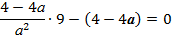
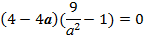
а=1, а=3, а=-3
5. Уравнение имеет два различных корня, тогда D>0.
4 - 4a> 0, тогда a<1
Ответ: а=-3
4.
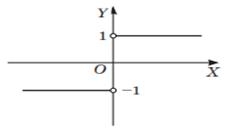
5.

Дата добавления: 2021-04-15; просмотров: 55; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
