МЭ олимпиады. Решения. 10 класс. 2017 год.

МЭ олимпиады. 10класс. 2015 год

1.Натуральные числа от 1 до 127 разбили на несколько (больше одной) групп. Оказалось, что во всех группах суммы чисел равны. Доказать, что число групп чётно.

2.Рациональные числа x и y таковы, что для них справедливо равенство x³+y³=2xy. Доказать, что число 1–xy является квадратом рационального числа.

3.Укажите все точки координатной плоскости xOy, через которые график функции 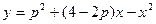не проходит ни при одном значении параметра p.

4.Четырёхугольник ABCD вписан в окружность с центром O. Точка P – точка пересечения диагоналей, точки K, L, M и N – соответственно, центры описанных окружностей треугольников AOP, BOP, COP и DOP. Доказать, что KL = MN.

5.Можно ли на плоскости можно расположить 2016 треугольников так, чтобы любые два из них имели непустое пересечение, но никакие три не имели общих точек?

МЭ олимпиады. 10класс. 2013год

1.Направление вращения Земли вокруг своей оси совпадает с направлением её вращения вокруг Солнца. Земной год составляет 365,25 суток. Сколько суток было бы в году, если бы Земля вращалась вокруг своей оси с той же скоростью, но в противоположном направлении? Земную ось считать перпендикулярной плоскости орбиты.

2.Решить в целых числах уравнение: 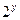= 1 + x + x²+ x³.

3.Три окружности k₁, k₂ и k₃ попарно касаются друг друга в трёх различных точках, не лежащих на одной прямой. Соединим точку касания окружностей k₁ и k₂ прямыми линиями с двумя другими точками касания. Доказать, что эти прямые пересекают k₃ в диаметрально противоположных точках.

4.Восемь мух, сидевших в восьми вершинах куба, одновременно взлетели, а через минуту снова сели в некотором новом порядке в разные вершины этого куба. Доказать, что среди этих мух найдутся такие три, которые до взлёта и после посадки образуют равные треугольники.

5.Даны два натуральных числа m и n. Доказать, что существует такое действительное число x, что дробные части чисел mx и nx лежат на отрезке [1/3; 2/3].

МЭ олимпиады. 10класс. 2016 год.

1.Докажите, что число 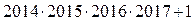является составным.

2.Сколько положительных чисел среди первых 100 членов последовательности: sin 1º, sin 10º, sin 100º, sin 1000º, …?

3.В треугольнике ABC AC = 18 см, BC = 21 см. Точка K является серединой стороны BC, а точка M серединой стороны AB, точка N лежит на стороне AC и AN = 6см. При этом MN = KN . Найдите длину стороны AB .

4.Докажите, что уравнение = 0 не имеет действительных корней.

5.Назовем число, большее 25, полупростым, если оно является суммой каких-то двух различных простых чисел. Какое наибольшее количество последовательных полупростых чисел могут оказаться полупростыми?

ШЭ олимпиады. 10 класс 2017 год

1.Несколько учащихся ушли из лицея и несколько пришли. В результате число учащихся уменьшилось на 10%, а доля мальчиков в лицее увеличилась с 50% до 55%. Увеличилось или уменьшилось число мальчиков?

2.Решите задачу Л. Эйлера: некий чиновник купил лошадей и быков за 1770 талеров. За каждую лошадь он уплатил по 31 талеру, а за каждого быка – по 21 талеру. Сколько лошадей и быков купил чиновник?

3.Найти множество значений параметра a, при которых дискриминант уравнения

ax²+2x+1 = 0 в 9 раз больше квадрата разности двух его различных корней.

4.Постройте график уравнения: .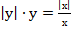

5.В окружность радиуса R вписан треугольник, вершины которого делят окружность в отношении 2:5:17. Найдите площадь треугольника.

МЭ олимпиады. Решения. 10 класс. 2017 год.

1. Сколько существует четырехзначных чисел, которые делятся на 17 и оканчиваются на 17?

2. В бесконечную арифметическую прогрессию с положительной разностью входят числа 25, 41, 65 (не обязательно стоящие рядом). Является ли членом этой последовательности число 2017? Обоснуйте.

3. В равнобедренной трапеции основания равны 9 см и 21 см, а высота 8 см. Найдите радиус описанной около трапеции окружности.

4. Пусть 0 < a < b < c < d . Могут ли уравнения 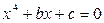и иметь общие корни?

5. Игра начинается с числа 2. За ход разрешается прибавить к имеющемуся числу любое натуральное число, меньшее его. Выигрывает тот, кто получит число 1000. Кто выиграет при правильной игре?

Год. Решения. 10 класс

1. Сумма S всех чисел равна S = 127×64. Число 127 – простое, а все делители числа 64, отличные от единицы – чётные. Поскольку во всех группах суммы чисел равны, общее число N групп является делителем числа S, то есть либо N=127, либо N чётно. Но равенство N = 127 означает, что в каждой группе ровно одно число, и поскольку все числа различны, такая ситуация невозможна.

2. Если x = 0, то 1 – xy = 1. Пусть x ¹ 0. Преобразуем величину 1 – xy, чтобы выделить комбинацию вида x³+y³. Для этого сначала домножим её на x²:

x²(1 – xy) = x² – x³y.

Вычитая и прибавляя y⁴, получим

x²(1 – xy) = x² – x³y – y⁴ + y⁴ = x² – y(x³ + y³) + y⁴ = x² – 2xy² + y⁴ = (x – y²)².

Из полученного равенства имеем: .

3.Рассмотрим данное уравнение как уравнение относительно неизвестного p при параметрах x и y. Преобразуя его, получим и . Это уравнение имеет решения в том и только том случае, когда левая часть неотрицательна, откуда следует ответ.

Ответ:все точки, для которых y < 4x – 2x².

4.Точки K, L, M и N лежат на серединном перпендикуляре m к отрезку OP. В частности, точка K получается как точка пересечения прямой m с серединным перпендикуляром к отрезку AP, остальные три точки получаются аналогично. Покажем, что середина F отрезка OP является также и серединой отрезка KM. Для этого опустим перпендикуляры KK₁, MM₁, FG и OH на прямую AC. Точка K1 – середина отрезка AP, M1 – середина PC, G – середина PH, а точка H – середина AC.

Получаем

По теореме Фалеса KF = FM.

Аналогично, F является и серединой отрезка LN, откуда следует требуемое утверждение.

5.Построим пример. Для этого рассмотрим на плоскости дугу единичной окружности w с угловой мерой p/2 и разделим её точками на 2015 равных дуг. В двух концевых точках и в 2014 точке деления проведём касательные, на которых отложим отрезки длины 4 так, что точки касания являются серединами построенных 2016 отрезков. Все построенные отрезки попарно пересекаются, при этом никакая точка пересечения двух отрезков не принадлежит никакому третьему отрезку, так как из одной точки плоскости можно провести только две касательных к данной окружности. Всего построенные отрезки имеют 2015×1008 точек попарного пересечения. Для отрезка s_i с номером i и точки пересечения M_jk отрезков с номерами j и k обозначим r_ijk расстояние от M_jk до s_i. Всего получается 2014×2015×1008 положительных чисел r_ijk, некоторые из которых равны. Среди перечисленных чисел есть наименьшее (это число – чрезвычайно мало, но оно всё-таки больше нуля). Обозначим его m. Теперь на каждом из построенных отрезков s_i как на катете построим прямоугольный треугольник D_i, второй катет которого равен m/2. Построение выполним так, чтобы прямая, содержащая больший катет, разделяла исходную единичную окружность и построенный треугольник. Все треугольники D_i, очевидно, попарно пересекаются. На рисунке представлена система из трёх таких треугольников. В полной системе треугольники ещё тоньше и примыкают друг к другу ещё плотнее.

Покажем, что никакие три из треугольников D_i не имеют общей точки. Действительно, никакая точка M_jk не содержится в треугольнике, построенном на отрезке s_i, для которого i ¹ j и i ¹ k. При этом, если прямая, содержащая катет s_i, отделяет окружность w от точки M_jk, то она отделяет от w также и пересечение треугольников, построенных на отрезках s_j и s_k. Поскольку точка M_jk удалена от s_I на расстояние, большее m, то как она сама, так и всякая точка пересечения треугольников D_j и D_k удалена от треугольника D_i на расстояние, большее m/2. Ответ: Да.

Год. МЭ. Решения. 10класс

1.Скорость вращения Земли вокруг своей оси можно измерять числом полных оборотов в год. При этом следует учитывать направление вращения. Будем считать, что направление вращения, совпадающее с направлением вращения вокруг Солнца положительно, а обратное ему – отрицательно. В такой интерпретации число суток в году, рассчитанное со знаком, зависит от скорости вращения Земли вокруг оси как линейная функция. Если бы Земля, вращаясь вокруг Солнца, совсем не вращалась вокруг своей оси, то Солнце в системе координат, связанной с Землёй, делало бы в год также ровно один оборот вокруг Земли, но в направлении с запада на восток. То есть, число суток в году уменьшилось бы на 366,25 и составило бы –1 сутки. Изменив скорость вращения ещё на такую же величину, мы ещё раз уменьшим число суток на 366,25. Получится –367,25. Знак минус означает, что в течение суток Солнце вращается с запада на восток. Абсолютная величина числа суток в году в этом случае равна 367,25.

Ответ: 367,25.

2.Разложив правую часть на множители, получим: 2^y = (1+x)(1+x²).Поскольку левая часть строго положительна, x ≥ 0. Решения (0; 0) и (1; 2) очевидны. Покажем, что других решений нет. Правая часть – произведение двух натуральных чисел, левая – степень двойки. Значит каждый из сомножителей в правой части – степень двойки. При x > 0 каждое из них чётно. Значит x нечётно. Нечётное число, возведённое в квадрат при делении на 4 даёт в остатке 1. Следовательно, при некотором целом k ≥ 0 выполняется равенство

1 + x² = 4k +2 = 2(2k+1). Правая часть может быть степенью двойки только при k = 0

Ответ: (0; 0), (1, 2).

3. Возможны два случая взаимного расположения окружностей. В одном случае все три окружности касаются друг друга внешним образом (рис. 1), в другом две окружности касаются между собой внешним образом и касаются третьей изнутри (рис. 2). На рисунках окружности k₁, k₂ и k₃ имеют центры соответственно в точках О₁, О₂ и О₃. Второй случай разбивается на два подслучая: точка касания k₁ и k₂ может быть точкой внешнего или внутреннего касания. Рисунок 2 соответствует второму подслучаю. Дальнейшее решение можно провести с применением гомотетии, или рассматривая треугольники. Первый способ позволяет не заботиться о разных случаях расположения окружностей.

Рис.1

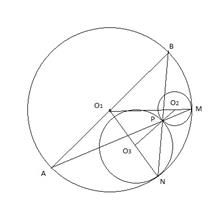
Рис.2

1 способ. Рассмотрим композицию трёх гомотетий H₁, H₂ и H₃. Гомотетия H₁ с центром в точке M касания окружностей k₁ и k₂ переводит k₁ в k₂; гомотетия H₂ с центром в точке P касания k₂ и k₃ переводит k₂ в k₃, и гомотетия с центром в точке N касания k₃ и k₁ переводит k₃ в k₁. В любом допустимом случае композиция H₃×H₂×H₁ является центральной симметрией с центром в точке O₁ – центре k₁. При этом точка A переходит при гомотетии H₁ в точку P касания k₂ и k₃, затем остаётся неподвижной, и на третьем шаге переходит в B. То есть точки A и B симметричны относительно O₁.

2 способ. Треугольник O₁MA подобен треугольнику O₂MP (равнобедренные треугольники с равными углами при основании). Из равенства углов ÐMO₁A=ÐMO₂P следует параллельность отрезков O₁A || O₂P. При этом лучи [O₁A) и [O₂P) противоположно направлены в случае внешнего касания окружностей k₁ и k₂, или сонаправлены в случае их внутреннего касания. Аналогично, из подобия треугольников O₁NB и O₃NP следует параллельность отрезков O₁B || O₃P. Лучи [O₂P) и [O₃P) либо сонаправлены, либо один из них является частью второго. Отсюда параллельность отрезков [O₁A] || [O₁B]. В любой из возможных конфигураций для попарного касания окружностей несложно убедиться, что лучи [O₁A) и [O₁B) противонаправлены. Отсюда утверждение задачи.

4. Рассмотрим двух мух, сидящих в вершинах на диагонали куба. Любая из оставшихся шести мух дополняет эту пару так, что три мухи сидят в трёх вершинах прямоугольного треугольника, причём все шесть таких возможных треугольников равны друг другу. Если выбранные две мухи после посадки окажутся снова на диагонали, то в качестве искомой тройки можно выбрать произвольную тройку, содержащую это пару. В противном случае следует выбрать третьей ту муху, которая после посадки оказалась по диагонали напротив первой из двух выбранных мух.

5.Если m = n, то можно взять x = 1/(2m). Пусть m < n. Если m = 1 и n = 2, то можно взять x = 1/3. Далее достаточно рассматривать случай, когда m и n – взаимно простые числа. Если m и n не взаимно просты, то поделив их на их наибольший общий делитель, мы сведём задачу к случаю взаимно простых чисел, после чего, поделив найденное значение x на НОД(m, n) получим решение задачи в общем случае.

Пусть 1 ≤ m < n, n ≥ 3 и числа m и n взаимно просты. В этом случае существуют такие целые числа p и q, что pm + qn = 1. Числа m/(2n), (m+2)/(2n), …, (m+2n)/(2n) разбивают на n равных частей числовой отрезок [m/(2n), (m+2n)/2n] длины 1, содержащий внутри себя число ½,. Каждая часть имеет длину 1/n. Выберем точку деления, ближайшую к числу ½. Пусть такая точка – это число (m+2k)/(2n). Тогда модуль разности |½ – (m + 2k)/(2n)| не превосходит 1/(2n) ≤ 1/6. Обозначим p’=kp и q’ = kq. Тогда

p’m+q’n = k;

p’m = k – q’n;

{(p’m)/n} = k/n.

Для

x = p’/n + 1/(2n)

получаем

{nx} = ½

{mx} = {(2p’m+m)/(2n)} = {(2k+m)/(2n)} Î [1/3, 2/3]. Требуемое число x найдено.

Геометрическая интерпретация решения. В системе координат (u,v) построим график функции u = (m/n)v с областью задания u ≤ n. Это отрезок прямой с угловым коэффициентом m/n, соединяющий точки (0,0) и (m, n).

Для каждого единичного квадрата координатной сетки, имеющего непустое пересечение с графиком, выполним его параллельный перенос так, чтобы левый нижний угол квадрата совместился с началом координат. Тогда единичный квадрат 0 ≤ u, v ≤ 1 разобьётся образами кусков графика на полосы со сторонами, параллельными графику. При таком разбиении существует точка, принадлежащая линиям разбиения, и удалённая от центра единичного квадрата как по оси u, так и по оси v, не более чем на 1/6. В качестве числа x выбирается абсцисса прообраза такой точки, поделённая на n.

Дата добавления: 2021-04-15; просмотров: 244; Мы поможем в написании вашей работы!

Поделиться с друзьями:

12 3 Следующая ⇒

Мы поможем в написании ваших работ!