Эмпирическая функция распределения

⇐ ПредыдущаяСтр 3 из 4Следующая ⇒

Пусть п_х — число наблюдений, при которых значение признака X меньше х. При объеме выборки, равном п, относительная частота события X < x равна n_х/n.

Определение 8. Функция F *( x ) = n_x / n , (15.49)

определяющая для каждого значения х относительную частоту события X < х, называется эмпирической функцией распределения или функцией распределения выборки.

В отличие от эмпирической функции распределения F *( x ) выборки функция распределения F ( x ) генеральной совокупности называется теоретической функцией распределения. Различие между ними состоит в том, что функция F ( x ) определяет вероятность события X < х, a F *( x ) — относительную частоту этого события. Из теоретических результатов общей теории вероятностей (закон больших чисел) следует, что при больших п вероятность отличия этих функций друг от друга близка к единице:

Нетрудно видеть, что F *( x ) обладает всеми свойствами F ( x ), что вытекает из ее определения (15.49):

• значения F *(х) принадлежат отрезку [0,1];

• F *( x ) является неубывающей функцией;

• если х₁ — наименьшая варианта, то F *( x ) = 0 при х ≤ x ₁;

• если х_к — максимальная варианта, то F *( x ) = 1 при х > х_к.

Сама же функция F *( x ) служит для оценки теоретической функции распределения F ( x ) генеральной совокупности.

Пример 3. Построить эмпирическую функцию по заданному распределению выборки:

Решение. Находим объем выборки: п =10 +15 + 25 = 50. Наименьшая варианта равна 2, поэтому F *( x ) = 0 при х ≤ 2. Значение X < 4 (или х₁ = 2) наблюдалось 10 раз, значит, F (x) = 10/50 = 0,2 при 2 < х < 4. Значения X < 6 (а именно х₁ = 2 и x₂ =4) наблюдались 10 + 15 = 25 раз, значит, при 4 < x < 6 функция F *( x ) = 25/50 = 0,5. Поскольку X= 6 – максимальная варианта, то F *( x )= 1 при х>6. Напишем формулу искомой эмпирической функции:

График этой функции показан на рисунке 15.8

Полигон и гистограмма

Каждую пару значений (х _i , n_i ) из распределения выборки можно трактовать как точку на координатной плоскости. Точно так же можно рассматривать и пары значений (x_i, Wi ) относительного распределения выборки. Ломаная, отрезки которой соединяют точки (х _i , n_i ), называется полигоном частот.

Ломаная, соединяющая на координатной плоскости точки (x_i , Wi), называется полигоном относительных частот. На рис. 15.9 показан полигон относительных частот для распределения, приведенного в примере 2.

Для случая непрерывного признака X удобно разбить интервал ( x_min , x_max ) его наблюдаемых значений на несколько частичных интервалов длиной h каждый и найти для каждого из этих интервалов сумму частот n_j, попавших в него.

Ступенчатая фигура, состоящая из прямоугольников с основаниями длиной h и высотами n_j / h (плотность частоты), называется гистограммой частот. Геометрический смысл гистограммы: нетрудно видеть, что площадь ее равна сумме всех частот или объему выборки. На рис. 15.10 изображена гистограмма объема п = 100.

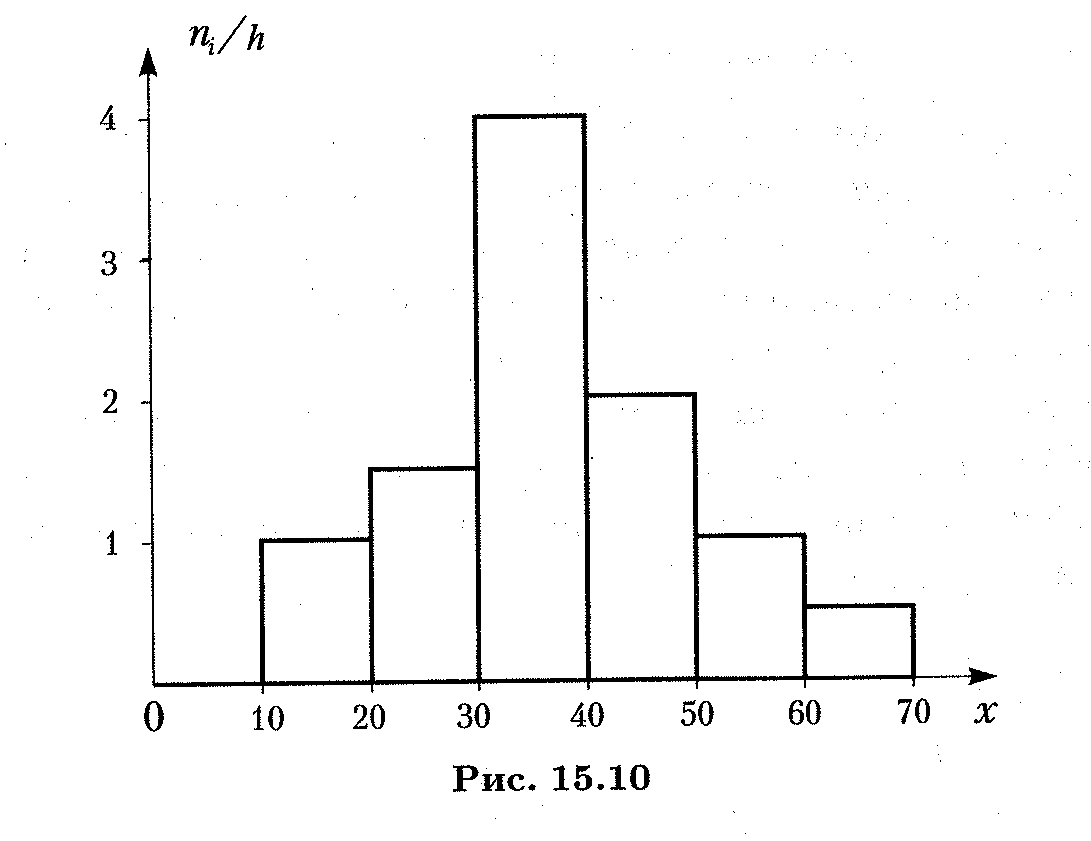Аналогичным образом определяется и гистограмма относительных частот; в этом случае высоты прямоугольников, составляющих ступенчатую фигуру, определяются отношениями сумм относительных частот, попадающих в интервал 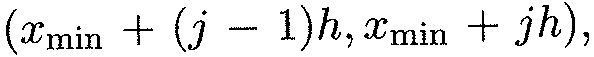к длине интервала h , т.е. величинами Wj / h . Нетрудно видеть, что площадь гистограммы относительных частот равна единице (сумме относительных частот выборки).

Одной из наиболее часто встречающихся задач, связанных с исследованием системы случайных величин, является задача выявления зависимости между этими случайными величинами. Наиболее простая — детерминированная функциональная зависимость между случайными величинами — на практике встречается редко. Как правило, между случайными величинами имеет место более сложная зависимость, когда изменение одной случайной величины обусловлено не только изменением другой, но влиянием множества других факторов, зачастую не поддающихся учету. Такая зависимость, при которой изменение одной величины приводит к изменению характеристик распределения другой величины, называется статистической.

Таким образом, статистическая зависимость между случайными величинами ХиУ может состоять из двух компонентов: функционального, обусловленного жесткой, детерминированной зависимостью между этими случайными величинами, и случайного, связанного с влиянием как раздельных для Хи 7случайных факторов, так и общих.

Взаимосвязь между случайными величинами определяется их корреляционным моментом к_ху или коэффициентом корреляции р_ху, а также уравнениями регрессии одной случайной величины на другую.

Рассмотрим методы определения названных характеристик системы случайных величин Л"и 7по их выборочным совокупностям.

Дата добавления: 2021-04-05; просмотров: 87; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 234 Следующая ⇒

Мы поможем в написании ваших работ!