Квантор существования – это выражения «существует», «некоторые», «найдется», «есть», «хотя бы один».
Обозначение : $ х – «существует х»
( $ х) Ах – «существует такое значение х, что А(х) – истинное высказывание».
Истинность высказывания с квантором существования устанавливается при помощи конкретного примера, а ложность - доказывается.
Квантор общности – это выражения «всякий», «любой», «каждый» и «все».
Обозначение: " х – для всякого х.
( " х) А(х) – «для всякого х предложения А(х) – истинное высказывание».
Истинность высказывания с квантором общности устанавливается путем доказательства, а ложность – контрпример.
Пример: «Всякое натуральное число делится на 2 » высказывание содержит квантор общности – «всякое и оно – Л, т.к. «3 не делится на 2» - контрпример.
В математике часто приходится строить предложения в которых что – либо отрицается.
Пример: «15 – простое число» А – Л
Построим отрицание высказывания: «неверно, что 15 простое число» - И. Обозначение: Ā
Читают: «Не А» или «Неверно, что А».
Определение. Отрицанием или инверсией высказывания А называется высказывание Ā, которое ложно, если высказывание А истинно, и истинно, если высказывание А- ложно.
Отрицании конъюнкции и дизъюнкции
Законы де Моргана
Чтобы построить отрицание конъюнкции (дизъюнкции), достаточно заменить отрицаниями составляющие её высказывания, а союз «и» («или») заменить союзом «или» («и»).
Пример: Предположим, что строгий Преподаватель ставит экзамен, если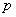 
– Студент ответил на 1-й вопрос и 
– Студент ответил на 2-й вопрос. Тогда высказывание 
, гласящее о том, что Студент не сдал экзамен, будет равносильно утверждению 
– Студент не ответил на 1-й вопрос или на 2-й вопрос.
|
|
|
Операции следования ( импликация) и равносильности (эквивалентность).
Рассмотрим высказывательные формы:
А(х) – «х >5»
В (х) – «х >2»
Как связаны между собой?
Можно утверждать:
Ø «Все числа больше пяти больше двух» или
Ø «из того, что х >5 следует, что х >2 ».
Определение. Высказывательная форма В (х) следует из высказывательной S формы А (х), если В (х) обращается в истинное высказывание при всех тех значениях х, при которых А (х) истинна.
Обозначение: А(х)ÞВ(х)
Читают:
• Из А(х) следует В;
• Всякое А(х) есть В(х);
• Если А (х), то В(х);
• В(х)есть следствие А(х);
• А(х) – достаточное условие для В (х)
• В(х) – необходимое условие для А(х)
• Как установить истинность предложения А(х)ÞВ(х)?
Его можно сформулировать в виде:
«Всякое А(х) есть В(х)»
Имеет место высказывание с квантором общности, значит истинность устанавливается путем доказательства, а ложность – контрпример.
Рассмотрим высказывания:
А(х) – «треугольник равнобедренный»
|
|
|
В(х) – «Углы при основании треугольника равны »
А(х) ÞВ (х) – И
«Если в треугольнике углы при основании равны, то он равнобедренный» - И
Говорят: предложения А(х) и В(х) – равносильны.
Определение. Предложения А(х) и В(х) равносильны, если из предложения А(х) следует предложения В(х), а из предложения В(х) следует предложение А(х).
Обозначение: А(х)ÛВ(х)
Читают:
• А(х) равносильно В(х)
• А(х) тогда и только тогда, когда В(х)
• А(х) – необходимое и достаточное условие В(х)
• В(х) – необходимое и достаточное условие А(х)
Дата добавления: 2021-04-06; просмотров: 150; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!