Свойства определенного интеграла

⇐ ПредыдущаяСтр 3 из 3

1) Интеграл от алгебраической суммы интегрированных на отрезке функций равен алгебраической сумме интегралов от каждой из них:

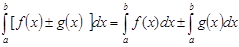
2) Постоянный множитель можно выносить за знак определенного интеграла

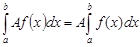
3) При перестановке пределов интегрирования определенный интеграл меняет знак на противоположный:

4) Определенный интеграл с одинаковыми пределами равен нулю:

5) Отрезок интегрирования можно разделить на части:

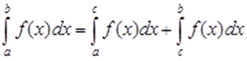
с-точка, лежащая между а и b.

6) Если 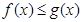на отрезке 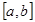, то .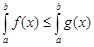

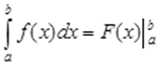Для вычисления определенного интеграла от функции 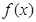, в том случае , когда можно найти соответствующую первообразную 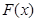, служит формула Ньютона-Лейбница:

=F(b)-F(a)

Формула Ньютона–Лейбница

Если функция y = f(x) непрерывна на отрезке [a, b] и F(x) – какая-либо ее первообразная на этом отрезке, то справедлива следующая формула:

где символ называется знаком двойной подстановки.

Пример:

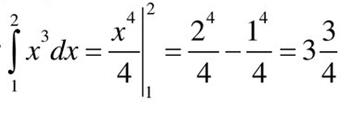
20. Дифференциальные уравнения первого порядка с разделяющимися переменными

Дифференциальное уравнение первого порядка y′=f(x,y) называется уравнением с разделяющимися переменными, если функцию f(x,y) можно представить в виде произведения двух функций f(x,y)=g(x)⋅h(y), по отдельности зависящих только от независимой переменной x и только от функции y.

Алгоритм решения ДУ с разделяющимися переменными:
1. Переписываем производные через y′=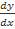

2. Разделяем все y в левую часть уравнения, а все x в правую

3. Интегрируем обе части уравнения

21. Понятие матрицы. Типы матриц (с примерами).

Матрица — математический объект, записываемый в виде прямоугольной таблицы элементов (например, целых, действительных или комплексных чисел), который представляет собой совокупность строк и столбцов, на пересечении которых находятся его элементы. Количество строк и столбцов задает размер матрицы.

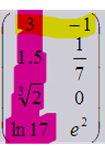
Желтым выделены строки (обозначаются буквой m), а розовым выделены столбцы (обозначаются буквой n). На пересечении них находится элемент матрицы под номером строки 1 и столбца 1, то есть а₁₁, равный 3.

Типы матриц:

Прямоугольная:

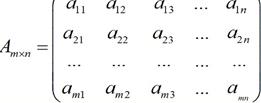
Квадратная (частный случай прямоугольной):

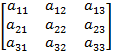
Как можно заметить, число столбцов n и число строк m равны. Данная матрица – 3го порядка. У квадратной матрицы также есть диагонали – главная (a₁₁, a₂₂, a₃₃) и побочная (a₃₁, a₂₂, a₁₃).
Вектор – строка:

Вектор строка есть матрица размером m строк и n = 1

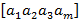
Вектор – столбец:

Вектор столбец есть матрица размером n столбов, и m = 1

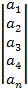
22. Линейные операции над матрицами.

· Алгебраическое сложение (оно же сложение и вычитание матриц)

Свойства сложения:

1. Для матриц А, В и С одного порядка характерно свойство ассоциативности сложения А + (В + С) = (А + В) + С.

2. Для матриц данного порядка существует нейтральный элемент по сложению, которым является нулевая матрица. То есть, справедливо свойство А + 0 =А.

3. Для ненулевой матрицы А данного порядка существует матрица (–А), их суммой является нулевая матрица: А + (-А) = 0.

4. Для матриц А и В данного порядка справедливо свойство коммутативности сложения: А + В = В + А.

· Произведение/деление на число отличное от нуля (в случае умножения на 0, получается так называемая нулевая матрица).

Свойства операции умножения матрицы на число:

1. Для матриц одного порядка А и В, а также произвольного действительного (или комплексного) числа 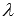справедливо свойство дистрибутивности умножения относительно сложения .

2. Для произвольной матрицы А и любых действительных (или комплексных) чисел 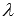и 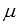выполняется свойство дистрибутивности .

3. Для произвольной матрицы А и любых действительных (или комплексных) чисел 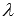и 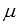справедливо свойство ассоциативности умножения .

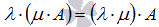4. Нейтральным числом по умножению на произвольную матрицу А является единица, то есть, .

Примеры:

Сложение/вычитание:

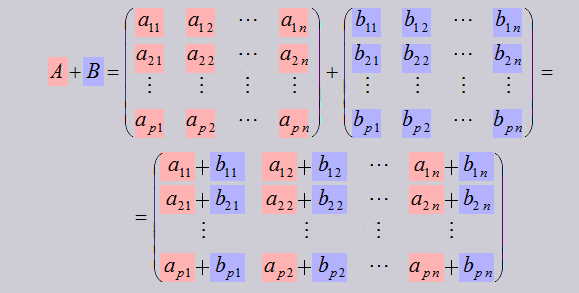
Умножение на число:

23. Произведение матриц.

Произведение матрицы А порядка 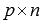и матрицы В порядка 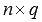- это такая матрица С порядка , каждый элемент которой равен сумме произведений элементов i -ой строки матрицы А на соответствующие элементы j-ого столбца матрицы В, то есть,

A * B B*A

Пример :

Найдите все элементы матрицы С, которая получается при умножении матриц

и .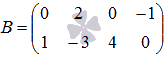

Решение.

Порядок матрицы А равен p=3 на n=2, порядок матрицы В равен n=2 на q=4, следовательно, порядок произведения этих матриц будет p=3 на q=4. Воспользуемся формулой

Последовательно принимаем значения i от 1 до 3 (так как p=3) для каждого j от 1 до 4 (так как q=4), а n=2 в нашем случае, тогда

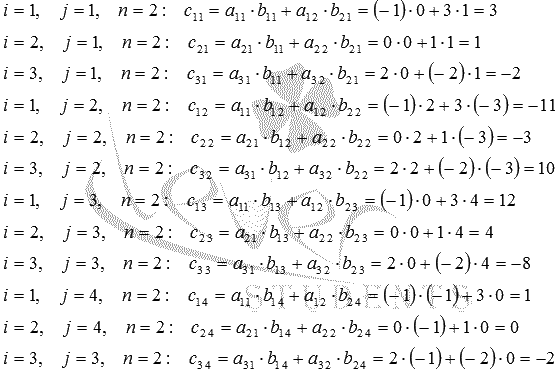
Так вычислены все элементы матрицы С, и матрица, полученная при умножении двух заданных матриц, имеет вид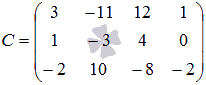

24. Транспонированная и обратная матрица.

Транспонированная матрица — матрица 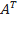{\displaystyle A^{T}}, полученная из исходной матрицы А {\displaystyle A}заменой строк на столбцы.

То есть, если у нас была матрица то станет

Свойства транспонированных матриц:
1) Дважды транспонированная матрица А равна исходной матрице А.

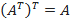
2) {\displaystyle (A^{T})^{T}=A}Транспонированная сумма матриц равна сумме транспонированных матриц.

3) {\displaystyle (A+B)^{T}=A^{T}+B^{T}}Транспонированное произведение матриц равно произведению транспонированных матриц, взятых в обратном порядке.

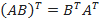
4) {\displaystyle (AB)^{T}=B^{T}A^{T}}При транспонировании можно выносить скаляр.

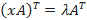
5) {\displaystyle (\lambda A)^{T}=\lambda A^{T}}Определитель транспонированной матрицы равен определителю исходной матрицы.

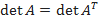
Пример :

Матрица называется обратной по отношению к данной, если ее умножение на исходную матрицу как справа, так и слева дает единичную матрицу.

Матрица называется особенной или выраженной, если ее определитель равен 0.

Матрица не особенная и не выраженная, если ее определить не равен 0.

Выраженная или особенная матрица не имеет обратной.

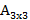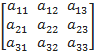
1. detA

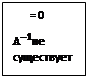detA – определитель матрицы.

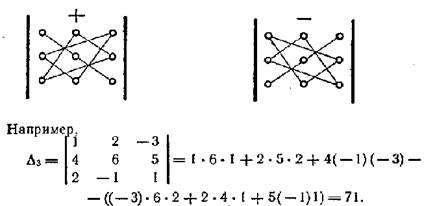
2. =

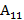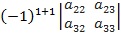
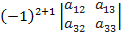
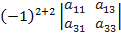
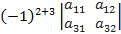
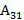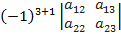
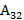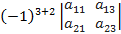
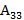3. 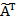= – транспонированная матрица

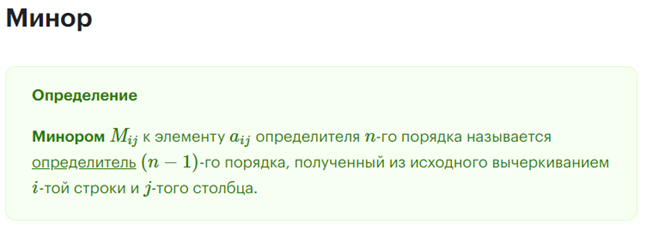
25. Миноры и алгебраические дополнения.

26. Ранг матрицы.

Ранг матрицы — наивысший порядок минора матрицы, отличный от нуля.

Алгоритм решения:

Если есть хотя бы один элемент матрицы, отличный от нуля, то ранг матрицы как минимум равен единице (так как есть минор первого порядка, не равный нулю).

Далее перебираем миноры второго порядка. Если все миноры второго порядка равны нулю, то ранг матрицы равен единице. Если существует хотя бы один ненулевой минор второго порядка, то переходим к перебору миноров третьего порядка, а ранг матрицы как минимум равен двум.

Аналогично, если все миноры третьего порядка равны нулю, то ранг матрицы равен двум. Если существует хотя бы один минор третьего порядка, отличный от нуля, то ранг матрицы как минимум равен трем, а мы преступаем к перебору миноров четвертого порядка.

И так далее.

Ранг матрицы не может превышать наименьшего из чисел p и n.

Пример.

Найдите ранг матрицы .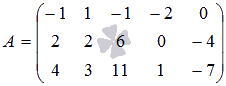

Решение.

Так как матрица ненулевая, то ее ранг не меньше единицы.

Минор второго порядка 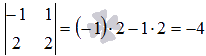отличен от нуля, следовательно, ранг. Переходим к перебору миноров третьего порядка:

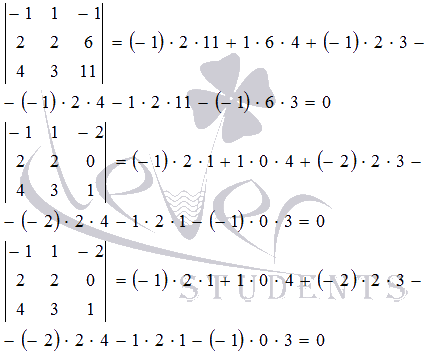
Все миноры третьего порядка равны нулю. Поэтому, ранг матрицы равен двум.

Ответ:

Rank(A) = 2.

27. Типы матричных уравнений и способ их решения.

Всего известно о 3 основных матричных уравнениях:

Пример.

Решение.

Данное уравнение имеет вид A ⋅ X = B, то есть в произведении матрицы A и неизвестной матрицы X матрица A находится слева. Поэтому решение следует искать в виде , то есть неизвестная матрица равна произведению матрицы B на матрицу, обратную матрице A слева. Найдём матрицу, обратную матрице A.

Сначала найдём определитель матрицы A:

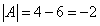Найдём алгебраические дополнения матрицы A:

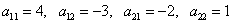Составим матрицу алгебраических дополнений:

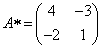Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A:

Теперь у нас есть всё, чтобы найти матрицу, обратную матрице A:

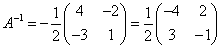Наконец, находим неизвестную матрицу:

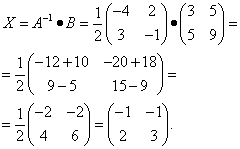
28. Логарифмическое дифференцирование (понятие метода).

Логарифмическим дифференцированием - называется метод дифференцирования функций, при котором сначала находится логарифм функции, а затем вычисляется производная от него. Такой прием можно использовать для нахождения производных степенных, рациональных и некоторых иррациональных функций.

29. Дифференциальные уравнения второго порядка

Дифференциальные уравнения второго порядка – это уравнение, содержащее производные не выше второго порядка.

y’’=f (x;y;y’)

Общее решение дифференциального уравнения второго порядка содержит 2 произвольные постоянные.

Примеры :

30. Числовые ряды. Сходимости и расходимости числовых рядов

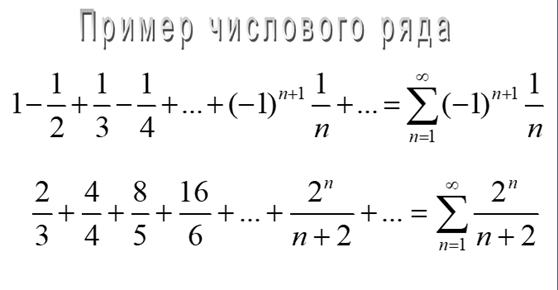
31. Необходимый и достаточный признаки сходимости с положительными членами

32. Степенной ряд. Разложение функции в ряд Маклорена

an*xⁿ - общий член ряда

Число R называется радиусом сходимости ряда, если при 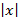<R ряд сходится и притом абсолютно, а при 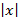>R ряд расходится.

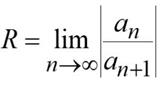
Промежуток (интервал) сходимости - -R<x<R

Если предел равен нулю (R=0), то ряд сходится в единственной точке x=0.

На концах промежутка ряд может сходится (абсолютно или условно), но может и расходится. Сходимость ряда при x=-R и x=R исследуется с помощью какого-либо из признаков сходимости.

Пример 1.

Найти область сходимости степенного ряда

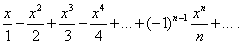
Решение.

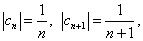
то есть

Найдём радиус сходимости данного ряда:

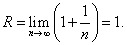Исследуем сходимость ряда на концах интервал.

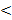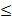Данный ряд сходится при x=1 и расходится при x=−1. Следовательно, областью сходимости служит -1 x 1.

Для разложени я функции в ряд Маклорена необходимо:

1. Вычеслить значние функции и е последовательных производных в точке x=0, т.е. f(0), f ’(0), f 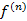’’(0),…, (0)

2. Составить ряд Мклорена, подставив значения функции и ее последовательных производных в формулу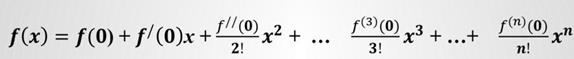

3. Найти прмежуток сходимости полученного ряда по формуле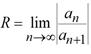

33. Тригонометрическая и показательная форма комплексного числа. Действия с комплексными числами.

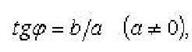
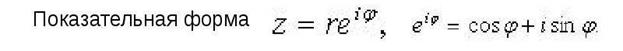
34. Задача Коши для обыкновенных дифференциальных уравнений.

Задача Коши – нахождение решения дифференциального уравнения при заданных начальных условиях. Для решения этой задачи нужно сначала решить дифф. уравнение в общем виде, а затем уже подставить заданные условия и получить решение, то есть найти константы (в отличие от обычных СЛАУ, решением уравнения будет не число, а функция).

Дата добавления: 2021-07-19; просмотров: 56; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 23

Мы поможем в написании ваших работ!