Исследование функции на монотонность с помощью производной
Понятие множества, виды множеств, подмножества (с примерами).
Множество – это совокупность некоторых объектов.
В математике изучаемое понятие обозначается заглавными латинскими буквами, например: А, С, Z, N, Q, A1, A2 и т. д.
Объекты, составляющие группу, называются элементами множества и записываются строчными латинскими буквами: a, b, c, d, x, y, a1, a2 и т. д.
Границы совокупности обозначаются фигурными скобками { }.
Принадлежность элементов множеству обозначается знаком – Є.
 Пример: N = {a, b, c, y}, а Є N – элемент «а» принадлежит N.
Пример: N = {a, b, c, y}, а Є N – элемент «а» принадлежит N.

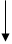

 | |||||
 | |||||
 | |||||
Подмножество данного множества – это множество, все элементы которого принадлежать данному множеству и обозначается знаком - ⊆.
Пример: А = {а, в, с, у} и В = {а, в, с, е, к} – все элементы А являются элементами совокупности В, следовательно, А ⊆ В.
Если множества состоят из одинаковых элементов, их называют равными.
Пример: А = {23, 29, 48} и В = {23, 29, 48}, тогда А = В.
2.Операции над множествами
Пересечение множеств – это множество все элементы которого принадлежат каждому из этих множеств. Обозначается знаком ∩.
 Применяются 2 закона:
Применяются 2 закона:
· Переместительный (A∩B; B∩A);
· Сочетательный (A∩(B∩C); AB∩C);
Пример: В = {1, 6, 17} и С = {2, 13, 18}, В ∩ С= {1, 2, 6, 13, 17, 18}.
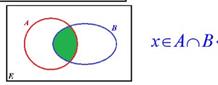
 Объединение множеств – это множество, состоящее из всех элементов, принадлежащих хотя бы одному из данных множеств. Обозначается значком ∪.
Объединение множеств – это множество, состоящее из всех элементов, принадлежащих хотя бы одному из данных множеств. Обозначается значком ∪.
|
|
|
Пример: В = {36, 42, 53, 64} и С = {32, 42, 55, 66}, В ∪ С = {42}.
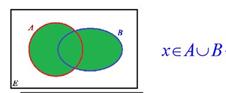
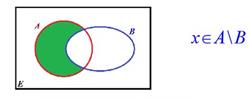 Разность множеств – это множество, все элементы множества А не принадлежащих множеству В. Обозначается значком /.
Разность множеств – это множество, все элементы множества А не принадлежащих множеству В. Обозначается значком /.
Пример: В = {12, 14, 16, 18} и С = {13, 14, 15, 17}, В / С = {14}. В случае, когда В / С = С /
3. Операции над высказываниями. Операция отрицания. Конъюнкция высказываний.
Отрицанием(инверсия) – это логическое операция, при котором если исходное логическое выражение истинно, то результат отрицания будет ложным, и наоборот.
Обозначение отрицания A¯ читается «не A».
0 – «ложь»,
1 – «истина»
| A | A¯ |
| 0 | 1 |
| 1 | 0 |
Конъюнкция – это логическая операция, истины тогда и только тогда, когда оба исходных высказываний истины.
Обозначение конъюнкции A ∧ B, читается «А и В».
| A | B | A ∧ B |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Операции над высказываниями. Дизъюнкция высказываний.
Дизъюнкция – логическая операция, которая ложно тогда и только тогда, когда ложны оба высказывания А и В.
Высказывание А∨B читается «А или В».
Операция дизъюнкции соответствует образованию нового высказывания из данных А и В соединением их связкой «или», где «или» понимается в соединительном (хотя бы одно), а не в разделительном (либо - либо) смысле.
|
|
|
| A | B | A ∨ B |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
5. Определение производной функции. Правило 4-х шагов. Производная постоянной.
Производная функции в точке — это предел отношения приращения функции Δf к приращению аргумента Δx, когда последняя стремится к нулю:
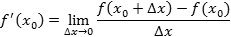
Общее правило дифференцирования:
1. Придавая аргументу x приращение Δx и подставляя в выражение функции вместо аргумента x наращенное значение x+Δx, находим наращенное значение функции: y+Δy=f(x+Δx).
2. Вычитая из наращенного значения функции ее первоначальное значение, находим приращение функции: Δy=f(x+Δx)-f(x).
3. Делим приращение функции Δy на приращение аргумента Δx, т. е. составляем отношение 
4. Находим предел этого отношения при Δx -> 0, т. е. 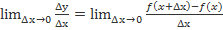 .
.
Этот предел и есть производная от функции y=f(x).
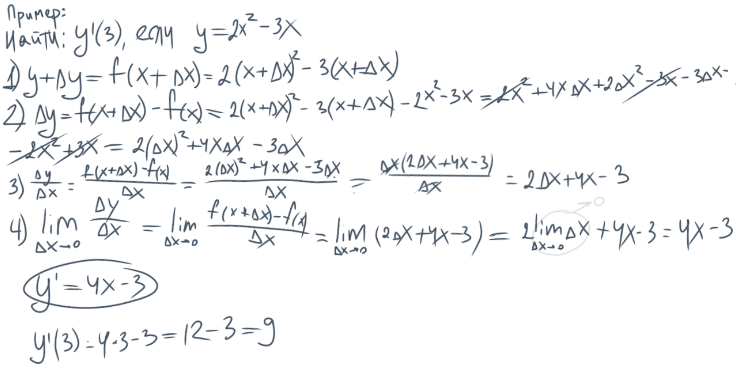
Производная постоянной равна нулю: C ' = 0
6. Производная линейной функции. Производная алгебраической суммы.
| Производная суммы функций равна сумме производных каждой из функций: (u+v)′=u′+v′ |


7. Производная произведений двух функций
Производная произведения равна произведению производной первого множителя на второй множитель плюс произведение первого множителя на производную второго множителя:
|
|
|
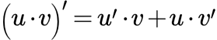


8. Производная частного двух функций. Вывести производную функций y = tgx
 Производная частного равна разности произведения производной числителя на знаменатель и произведения числителя на производную знаменателя, деленной на квадрат знаменателя.
Производная частного равна разности произведения производной числителя на знаменатель и произведения числителя на производную знаменателя, деленной на квадрат знаменателя. 


9. Производная функции y = sinx , y = ctgx
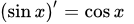


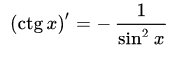


Исследование функции на монотонность с помощью производной
1. Функция называется возрастающей если большему значению аргумента соответствует большее значение функции.
x₂ > x₁ => f(x₂) > f(x₁)
∆x> 0; ∆f(x)> 0
2. Функция убывает, если большему значению аргумента соответствует меньшее значение функции
∆x> 0 => ∆f(x) <0
Вид монотонности зависит от знака первой производной этой функции
f’(x) > 0 => «+» => возрастает
f’(x) < 0 => «-» => убывает
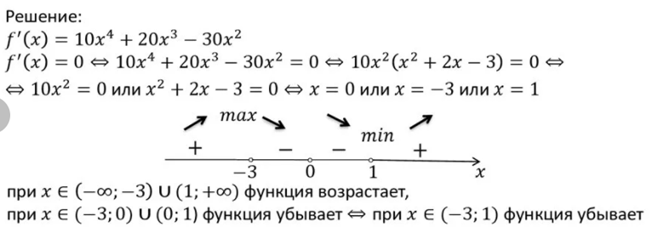
План решения задач :
1. f’(x)=?
2. Решить уравнение f’(x) = 0
3. 
4. f(x) возрастает на (-∞; x₁] и на [x₂; +∞)
f(x) убывает на [x₁; x₂]
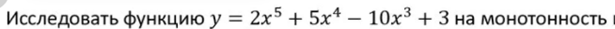
Дата добавления: 2021-07-19; просмотров: 73; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
