Исследование функции на экстремум с помощью производной
2 вида: максимум Xmax и минимум Xmin
Ymin = Xmin
Ymax = Xmax
Вид экстремума зависит от смены знака первой производной:
«+» => «-» ==> Xmax
«-» => «+» ==> Xmin
ЕСЛИ ЗНАК НЕ МЕНЯЕТСЯ, ЗНАЧИТ НЕТ ЭКСТРЕМУМОВ
План решения задач:
1. f’(x)=?
2. Решить уравнение f’(x) = 0
3. 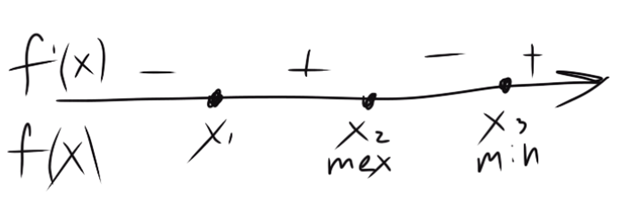
f(max) = f(x2)
f(min) = f(x3)

Исследование функции на выпуклость и вогнутость. Точки перегиба
Направление графика функции зависит от знака второй производной:
f’’(x) > 0 => «+» ==> выпуклость графика вниз
f’’(x) < 0 => «-» ==> выпуклость графика вверх
Точка перегиба – точка графика, в которой происходит смена направления выпуклости.
(x₀; f(x₀)) – точка перегиба
План решения задач:
1. f’(x)=?
2. f’’(x)=?
3. Решить уравнение f’’(x) = 0
4. 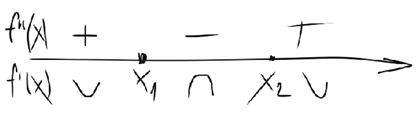
Пример:
y=x⁵-x+5
y’=5x⁴-1; y”=20x³
y”(0)=20x³ => x=0
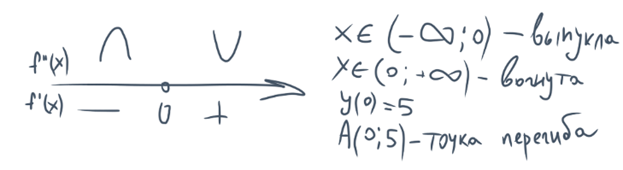
Общая схема исследования функции.
Порядок исследования:
1. Область определения функции. (ООФ – множество значений которые может принимать аргумент X)
2. Множество значений функции. (ОЗФ- область значений переменной Y)
3. 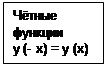
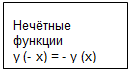 Определить четная или нечетная функция.
Определить четная или нечетная функция.
 | |||
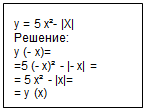 | |||
В остальных случаях функция общего вида.
4. Периодичность функции. (Функцияпериодична, если некоторый набор ее значений повторяется раз за разом, и точки с одинаковыми значениями функции расположены на числовой оси с равными промежутками)
5. Нули функции – корни. (Нулями функции называются значение абсциссы, при котором значение функции равно нулю.)
|
|
|
6. Промежутки знакопостоянства. (Промежутки, на которых значения функции имеют постоянный знак положительный или отрицательный).
7. Вид монотонности. (Промежутками монотонности функции называются интервалы, на которых она возрастает или убывает.)
8. Экстремумы функции. (Точки максимума и минимума функции на оси OХ.)
9. Наибольшее и наименьшее значение функции. (Самое большое значение У и самое малое значение У)
10. Направление выпуклости. (Вниз или вверх, характеризуется знаком ее второй производной. Точка графика функции, разделяющая промежутки выпуклости противоположных направлений этого графика, называется точкой перегиба.)
11. Асимптоты (Это прямая, к которой бесконечно близко приближается график функции. Асимптоты бывают горизонтальные, вертикальные и наклонные.)
Первообразная. Неопределенный интеграл и его свойства.
Первообразная функции представляет собой такую функцию, производная которой соответствует исходной функции.
Пример:
f производная функции F
F первообразная для функции f
Неопределенный интегралдля функции — это общая сумма всех первообразных данной функции.

Таблица интегралов.
|
|
|

Свойства.
1. Дифференциал от неопределенного интеграла равен подынтегральному выражению
Пример: d (∫ x 2 dx )= x 2 dx
2. Производная от неопределенного интеграла равна подынтегральной функции
Пример: (∫ f ( x ) dx ) ′ = f ( x )
3. Неопределенный интеграл от дифференциала некоторой функции равен этой функции плюс произвольная постоянная
Пример: ∫dF(x)=∫F′(x)dx=F(x)+C
4. Постоянный множитель можно выносить за знак неопределенного интеграла или вносить под знак интеграла
Пример: ∫α ⋅ f(x)dx=α∫f(x)dx
5. Неопределенный интеграл от суммы/разности двух и больше функций равен сумме/разности неопределенных интегралов от этих функций
Пример: ∫(f(x)±g(x))dx=∫f(x)dx±∫g(x)dx
15. Физический и геометрический смысл производной. Уравнение касательной к нормали.
Физический смысл:

Геометрический смысл: 

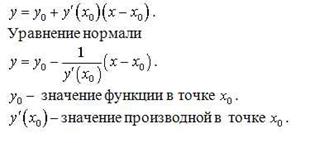 Уравнение касательной – это прямая, которая задается формулой. Любая прямая, в том числе и касательная, определяется двумя числами: и исходя из геометрического смысла производной (тангенс угла наклона касательной) – это есть угловой коэффициент
Уравнение касательной – это прямая, которая задается формулой. Любая прямая, в том числе и касательная, определяется двумя числами: и исходя из геометрического смысла производной (тангенс угла наклона касательной) – это есть угловой коэффициент
Нормаль - это перпендикуляр к касательной
16. Интегрирование методом подстановки (замены).
|
|
|
Идея метода замены состоит в том, чтобы сложное выражение (или некоторую функцию) заменить одной буквой.
Примеры:
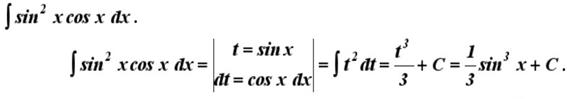
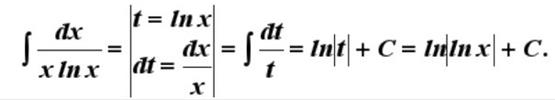
17. Интегрирование тригонометрических функций.
Вспомнить:

1. 
 Используется формулы понижения степени
Используется формулы понижения степени
2. 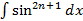 или
или 
· Отделить один множитель ( 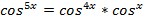 )
)
· Ввести новую переменную
3. 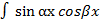 dx
dx
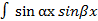 dx
dx
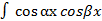 dx,
dx,
где 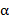 , β – действительные числа.
, β – действительные числа.
 dx=
dx=  [
[ 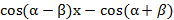 x]
x]
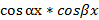 dx=
dx=  [
[  x]
x]
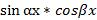 dx=
dx=  [
[ 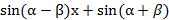 x]
x] 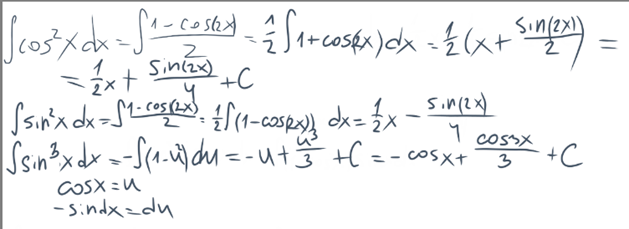
18. Интегрирование по частям. Интегрирование квадратного трёхчлена.
Метод интегрирования по частям используется тогда, когда нужно упростить имеющийся неопределенный интеграл или свести его к табличному значению.

Пример:
Вычислите неопределенный интеграл ∫ln(x)dx. 
Интегрирование квадратного трехчлена.





19. Определённый интеграл и его свойства. Формула Ньютона-Лейбница.
Пусть функция f ( x ) определена на отрезке a 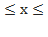 b . Разобьем этот отрезок на n частей a < x ₀< x ₁< x ₂<…<
b . Разобьем этот отрезок на n частей a < x ₀< x ₁< x ₂<…< 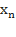 = b , выберем на каждом элементарном отрезке
= b , выберем на каждом элементарном отрезке  произвольную точку
произвольную точку 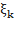 и обозначим через
и обозначим через  длину каждого отрезка. Интегральной суммой на отрезке a
длину каждого отрезка. Интегральной суммой на отрезке a 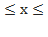 b называется сумма вида:
b называется сумма вида: 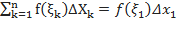 +
+ 
Определенным интегралом от функции f ( x ) на отрезке a 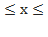 b называется предел интегральной суммы при условии, что длина наибольшего из элементарных отрезков стремится к нулю:
b называется предел интегральной суммы при условии, что длина наибольшего из элементарных отрезков стремится к нулю:
|
|
|
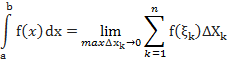
Для любой функции f ( x ), непрерывной на отрезке a 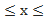 b , всегда существует определенный интеграл
b , всегда существует определенный интеграл 
Дата добавления: 2021-07-19; просмотров: 51; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
