Определитель квадратной матрицы равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения.
Указанные в теореме разложения выглядят следующим образом:
а) по элементам i строки , i=1,…, n:

б) по элементам j столбца, j=1,…, n:

Значение теоремы Лапласа состоит в том, что эта теорема позволяет свести вычисление определителей n-го порядка к вычислению более простых определителей (n-1) –го порядка.
Пример: Вычислить определитель четвертого порядка по теореме Лапласа
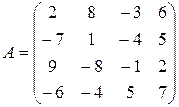
Решение:

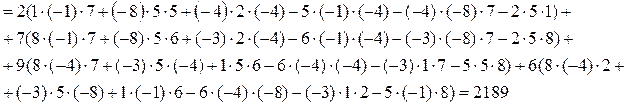
Замечание: С помощью теоремы Лапласа можно вычислять и определитель третьего порядка.
Пример: Вычислить по теореме Лапласа определитель матрицы третьего порядка
 .
.
Решение:
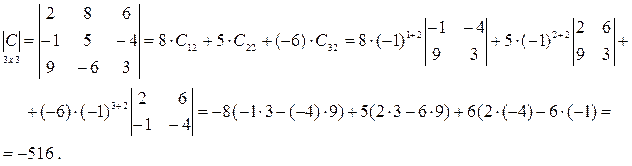
Свойства определителей.
Для упрощения вычисления определителей используют следующие свойства определителей.
1) Если какая-либо строка (столбец) матрицы состоит из одних нулей, то ее определитель равен 0.
Пример:
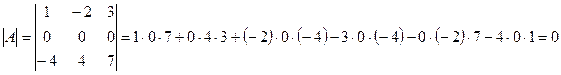 .
.
2) Если все элементы какой-либо строки (столбца) матрицы умножить на число 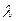 , то и определитель матрицы умножится на это число
, то и определитель матрицы умножится на это число 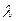 .
.
Замечание. За знак определителя можно выносить общий множитель элементов любой строки или столбца.
Примеры: 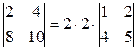 ;
;
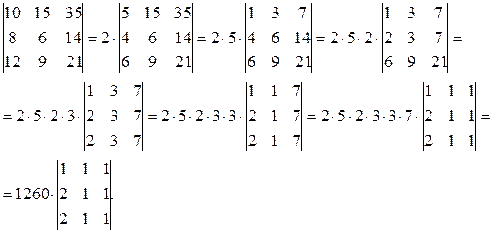
3) При транспонировании матрицы ее определитель не изменяется: 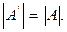
Пример:
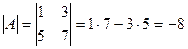 ;
; 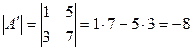 .
.
4) При перестановке двух строк (столбцов) матрицы ее определитель меняет свой знак на противоположный.
Пример:
 ;
; 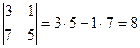 ;
; 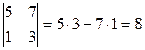 .
.
|
|
|
5) Если квадратная матрица содержит две одинаковые строки (столбца), то ее определитель равен 0.
Пример:
 .
.
6) Если элементы двух строк (столбцов) матрицы пропорциональны, то ее определитель равен 0.
Пример: Воспользуемся при вычислении свойствами 2) и 5) определителей:

7) Определитель матрицы не изменяется, если к элементам какой-либо строки (столбца) матрицы прибавить элементы другой строки (столбца), предварительно умноженные на одно и то же число.
Пример: Вычислить определитель матрицы С и матрицы С 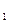 , полученной из матрицы С прибавлением ко второй строке матрицы С ее первой строки, умноженной на число -2:
, полученной из матрицы С прибавлением ко второй строке матрицы С ее первой строки, умноженной на число -2:

Воспользуемся уже полученным результатом определителя матрицы С:

Преобразуем матрицу С согласно свойству: 
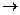
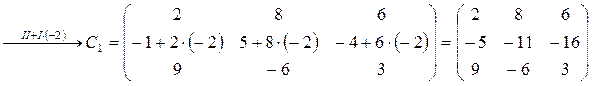 .
.
Теперь вычислим определитель получившейся матрицы:
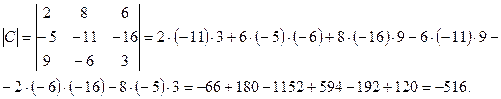
Решение:
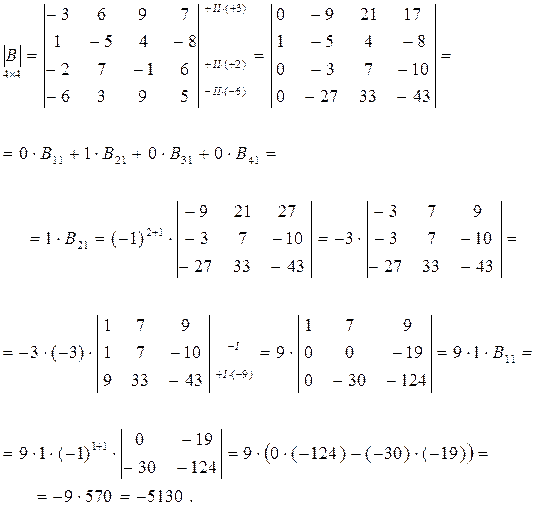
III . «ОБРАТНАЯ МАТРИЦА».
Определение: Матрица 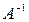 называется обратной по отношению к квадратной матрице
называется обратной по отношению к квадратной матрице 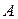 , если при умножении матрицы
, если при умножении матрицы 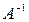 на матрицу
на матрицу 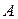 как справа, так и слева, получается единичная матрица:
как справа, так и слева, получается единичная матрица: 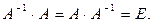
Замечание: Только квадратная матрица имеет обратную. Матрица, обратная данной, тоже квадратная.
Определения: 1. Если определитель матрицы 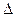 ≠ 0, то матрица называется невырожденной или неособенной.
≠ 0, то матрица называется невырожденной или неособенной.
|
|
|
Если определитель матрицы 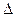 =0, то матрица называется вырожденной или особенной.
=0, то матрица называется вырожденной или особенной.
2. Присоединенная матрица 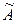 , получается из матрицы
, получается из матрицы  , транспонированной по отношению к матрице
, транспонированной по отношению к матрице 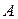 , заменой элементов матрицы
, заменой элементов матрицы  на их алгебраические дополнения.
на их алгебраические дополнения.
Теорема (необходимое и достаточное условие существования обратной матрицы):
Обратная матрица  существует и единственна тогда и только тогда, когда матрица
существует и единственна тогда и только тогда, когда матрица  невырожденная, т.е.
невырожденная, т.е.  . Ее элементы вычисляются по формуле:
. Ее элементы вычисляются по формуле:  .
.
Алгоритм построения обратной матрицы
1. Вычислим определитель данной матрицы 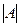 . Если . Если  , то для
данной матрицы не существует обратной.
2. Если , то для
данной матрицы не существует обратной.
2. Если  , строим матрицу , строим матрицу 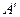 , транспонированную по отношению к матрице , транспонированную по отношению к матрице  , заменяя строки матрицы А ее столбцами.
3. Строим присоединенную матрицу , заменяя строки матрицы А ее столбцами.
3. Строим присоединенную матрицу 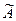 , заменяя элементы матрицы , заменяя элементы матрицы 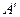 их алгебраическими дополнениями по формуле их алгебраическими дополнениями по формуле 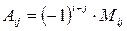 4. Вычисляем обратную матрицу по формуле
4. Вычисляем обратную матрицу по формуле 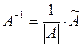 5. При необходимости проверяем правильность вычисления обратной матрицы
5. При необходимости проверяем правильность вычисления обратной матрицы  , исходя из ее определения , исходя из ее определения 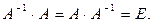 . .
|
Пример: 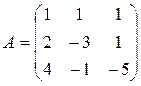 . Найти . Найти 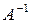 . .
|
1. 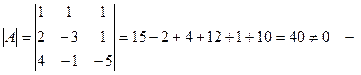 данная матрица имеет обратную. данная матрица имеет обратную.
|
2. 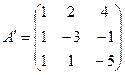 . .
|
3.  ; ;  ; ; 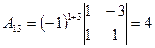 ; ;
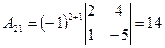 ; ; 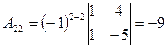 ; ;  ; ;
 ; ; 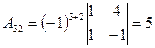 ; ; 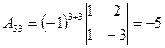 .
Получили присоединенную матрицу: .
Получили присоединенную матрицу:
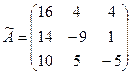 . .
|
4.  . .
|
Дата добавления: 2021-07-19; просмотров: 77; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
