Построение модели множественной регрессии для всех переменных

⇐ ПредыдущаяСтр 2 из 4Следующая ⇒

Выберем из меню Relate пункт Multiple Regression. В окне диалога множественной регрессии с помощью кнопки со стрелкой активизируем поле Dependent Variable (зависимая переменная). Затем в списке переменных, находящемся слева, используя прокрутку, найдем требуемую переменную. Пусть в рассматриваемом случае это будет акцентуация характера z8 — «возбудимость». Дважды щелкнем на этой переменной и она появится в активном поле.

Выделим в списке переменных из левого поля окна Multiple Regression переменные rr1‑rr12 и нажмем кнопку со стрелкой, указывающую на поле Independent Variables (независимые переменные). Все маркированные переменные будут включены в анализ (Рис. 6. 4). Нажмем кнопку OK.

Рис. 6. 4. Ввод данных в множественный регрессионный анализ

После того, как мы нажали кнопку OK, на экран выдается сводка проведенного анализа (Рис. 6. 5).

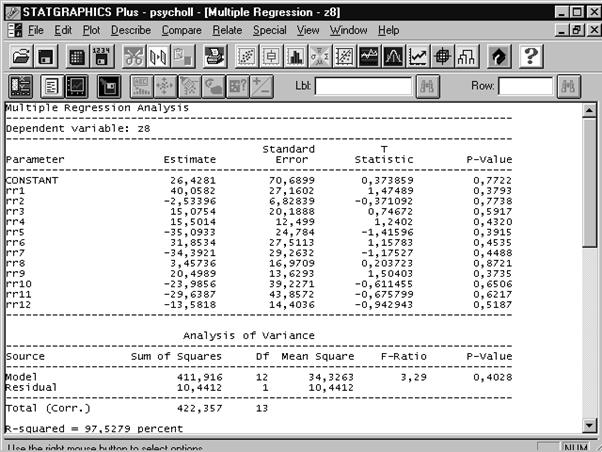
Рис. 6. 5. Сводка множественного регрессионного анализа

Из представленной сводки мы получаем сведения: об оценках величины константы и весовых коэффициентов в уравнении регрессии, о стандартных ошибках, Т‑статистиках и p‑значениях для полученных величин. Но главное, на что следует обратить внимание — это высокое p‑значение во второй таблице «Analysis of Varians» (Анализ дисперсии), где оценивается модель в целом. Оно составляет 0,4028, что говорит об очень низкой статистической значимости построенной модели. Это неудивительно, ведь, используя 12 переменных, мы имеем выборку объемом всего 14 человек. Путь, по которому следует идти в данном случае — это попытаться снизить количество переменных в правой части уравнения регрессии, применив метод пошагового отбора.

Пошаговый отбор переменных

Щелкнем правой кнопкой мыши и выберем из появившегося меню пункт Analysis Options. В разделе Fit окна диалога установим переключатель в положение Forward Selection (алгоритм последовательного увеличения группы переменных). Все остальное оставим без изменений (Рис. 6. 6). Нажмем OK. Получаем новую сводку регрессионного анализа (Рис. 6. 7). Как видно из таблиц, построена регрессионная модель, обладающая высокой статистической значимостью и объясняющая почти 66,9 % дисперсии зависимой переменной z1.

Рис. 6. 6. Окно диалога для задания параметров процедуры пошаговой регрессии

Опробуем теперь процедуру с последовательным уменьшением группы переменных. Выберем Analysis Options в контекстном меню.Установим переключатель Fit в положение Backward Selection и снимем флажок Constant in Model. Остальные элементы управления оставим без изменений. Получим следующую сводку результатов работы процедуры (Рис. 6. 8).

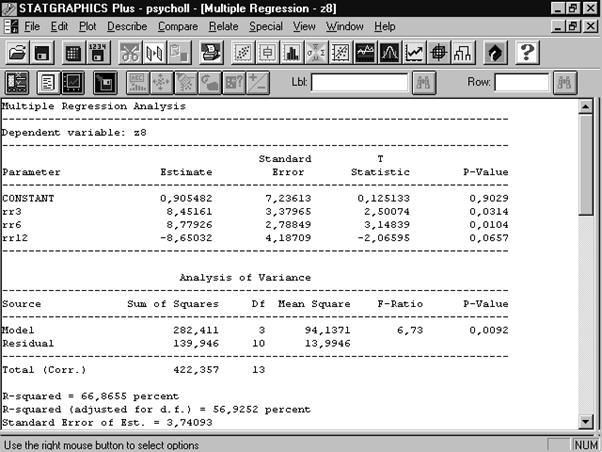
Рис. 6. 7. Сводка регрессионного анализа с пошаговым добавлением переменных

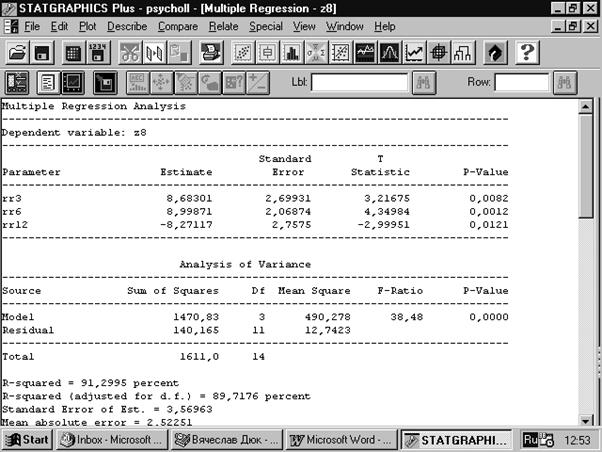
Рис. 6. 8. Результаты работы процедуры последовательного уменьшения группы переменных

Видно, что построенная регрессионная модель обладает значительно лучшими свойствами, чем предыдущая. В нее вошли три переменные: rr3 (желудок), rr6 (тонкий кишечник) и с обратным знаком rr12 (печень). Данная модель объясняет уже 91 % дисперсии зависимой переменной; также высок (89,7 %) коэффициент детерминации, скорректированный с учетом степеней свободы (adjusted R‑squared). При этом взаимоотношения переменных, зафиксированные в модели заслуживают почти 100‑процентного доверия.

Отобразим графически полученные результаты. Для этого нажмем кнопку графических опций (третья слева в нижнем ряду) и в окне диалога установим флажок Observed versus Predicted (наблюдение — предсказание). Нажмем OK (Рис. 6. 9). На экране образуется второе окно с требуемым графическим отображением. Раскроем его на весь экран, щелкнув дважды левой кнопкой мыши на заголовке (Рис. 6. 10).

Рис. 6. 9. Окно графических параметров

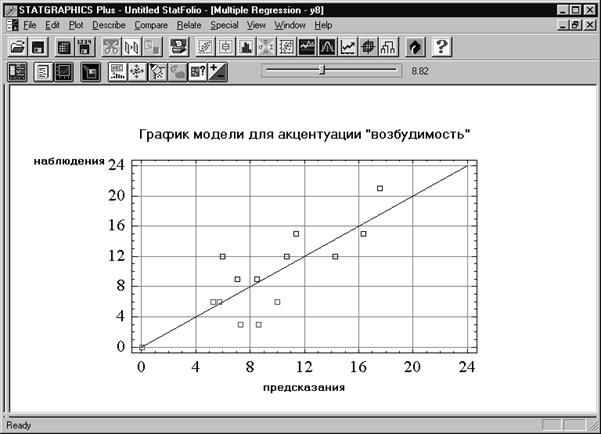
Рис. 6. 10. Графическое отображение регрессионной модели

Резюме

Представленный пример демонстрирует эффективность процедур последовательного увеличения и уменьшения группы переменных при построении моделей множественной регрессии. Удается подбирать модели, содержащие гораздо меньше переменных по сравнению с исходным множеством и имеющие более лучшие статистические характеристики. Незначительное количество переменных позволяет легко интерпретировать содержания регрессионных моделей. Так, в нашем случае уравнение регрессии после применения процедуры уменьшения группы переменных выглядит следующим образом

z8 = 8,7 (желудок) + 9,0 (тонкий кишечник) – 8,3 (печень)

Итак, можно предположить, что для людей с повышенной возбудимостью характерной реакцией на функциональную пробу является повышение активности желудка и тонкого кишечника при одновременном угнетении функции печени. И наоборот организм людей с пониженной возбудимостью реагирует на нагрузку снижением активности работы желудка и тонкого кишечника при одновременном увеличении активности работы печени.

Полученные данные в настоящее время подвергаются дальнейшим проверкам. Их окончательное подтверждение сулит значительные перспективы в следующих областях:

1. Собственно психодиагностика. Трудоемкая и громоздкая процедура психологического тестирования, сопровождаемая возможностями преднамеренных и непреднамеренных фальсификаций, заменяется в ряде случаев оперативной и объективной процедурой измерения электрокожного сопротивления в биологически активных точках с последующей релевантной обработкой.

2. Психотерапия. Раскрытие взаимосвязей особенностей функционирования органов человека с его психическими свойствами на количественном уровне создает предпосылки для создания эффективных методик психокоррекции.

3. Психогигиена и психопрофилактика. Электропунктурная психодиагностика вследствие объективности измерений позволяет на ранних стадиях обнаруживать нежелательные тенденции в психическом статусе.

4. Мониторинг психического состояния. Оперативная процедура электропунктурной психодиагностики дает возможность отслеживать изменения психического состояния в реальном времени.

5. Соматическая медицина. Раскрытие взаимосвязей психики и соматики создает предпосылки для разработки методик направленного соматического воздействия через создание определенных психических состояний с учетом межполушарной асимметрии мозговых процессов.

Приведенный список можно было бы продолжить вплоть до исследований генетической обусловленности психических особенностей человека и поиска границы, начиная с которой психическое становится самостоятельной сущностью. По‑видимому, для этого настанет свое время.

Дискриминантный анализ

Если критериальный показатель z измерен в номинальной шкале или связь этого показателя с исходными признаками является нелинейной, то для раскрытия закономерностей в данных и построения решающих правил используются методы дискриминантного анализа. В этом случае объекты в соответствии с внешним критерием разбиваются на группы (классы) и пространство признаков рассматривается под углом зрения способности разделять (дискриминировать) выделенные классы.

Большая группа методов дискриминантного анализа основана на байесовской схеме принятия решений о принадлежности объектов к тем или иным классам. Байесовский подход базируется на предположении, что задача сформулирована в терминах теории вероятностей и известны все представляющие интерес величины: априорные вероятности 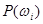для классов 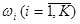и условные плотности распределения значений вектора признаков 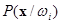. Правило Байеса заключается в нахождении апостериорной вероятности, 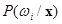, которая вычисляется следующим образом

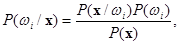
где

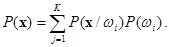
Решение о принадлежности объекта x_k к классу w_j принимается при выполнении условия, обеспечивающего минимум средней вероятности ошибки классификации:

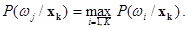
Для бинарных признаков, с которыми часто приходится иметь дело, принимающих значение 0 либо 1, p‑мерный вектор признаков x может принимать одно из 2ⁿ дискретных значений v₁, … , v_n. Функция плотности 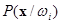становится сингулярной и заменяется на 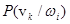— условную вероятность того, что x = v_k при условии класса w_i.

Другие подходы в дискриминантном анализа используют геометрические представления о разделении классов в пространстве признаков. Это следующие представления.

Совокупность объектов, относящихся к одному классу, образует «облако» в p‑мерном пространстве, задаваемом исходными признаками. Для успешной классификации необходимо, чтобы /Енюков И. С., 1986/:

a) Облако из w_i в основном было сконцентрировано к некоторой области D_i пространства признаков;

b) В область D_i попала незначительная часть «облаков» объектов из других классов.

Построение решающего правила рассматривают как задачу поиска K непересекающихся областей 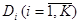, удовлетворяющих условиям a) и b). Дискриминантные функции (ДФ) определяют эти области посредством описания их границ в пространстве признаков.

Если какой‑либо объект попадает в область D_i, то будем считать, что принимается решение о его принадлежности к классу w_i. Обозначим P(w_i/ w_j) — вероятность того, что объект из класса w_j ошибочно попадает в область D_i. Тогда критерием правильного определения областей D_i будет

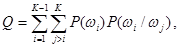
где P(w_i) — априорная вероятность появления объекта из w_i.

Приведенный критерий называют критерием средней вероятности ошибочной классификации. Его минимум достигается при использовании, в частности, рассмотренного выше байесовского подхода, который, однако, реализуется лишь при невысоких размерностях пространства признаков.

В теории анализа многомерных данных всесторонне разработаны процедуры построения линейных дискриминантных функций (ЛДФ), обеспечивающих при определенных предположениях минимум критерия средней вероятности ошибочной классификации. Так для случая двух классов w₁ и w₂ методы построения (ЛДФ) опираются на два предположения.

Первое состоит в том, что области D₁ и D₂, в которых концентрируются объекты из двух классов могут быть разделены (p – 1)‑мерной гиперплоскостью

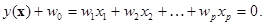
Коэффициенты w_i в данном случае интерпретируются как параметры, характеризующие наклон гиперплоскости к координатным осям, а w₀ называются порогом и соответствует расстоянию от гиперплоскости до начала координат. Преимущественное расположение объектов одного класса, например w₁, по одну сторону гиперплоскости выражается в том, что для них выполняется условие y(x) < 0, а для объектов другого класса w₂ — обратное условие y(x) > 0.

Второе предположение касается критерия качества разделения областей D₁ и D₂ гиперплоскостью y(x) + w₀ = 0. Наиболее часто предполагается, что разделение будет тем лучше, чем дальше отстоят друг от друга средние значения случайных величин 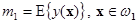и 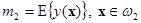, где E{ × } — оператор усреднения.

В простейшем случае полагают, что классы w₁ и w₂ имеют одинаковые ковариационные матрицы S₁ = S₂ = S. Тогда вектор оптимальных весовых коэффициентов w определяется следующим образом /Андерсон Т., 1963/

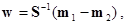
где m_i — вектор средних значений признаков для класса w_i.

Для определения величины порога w₀ вводят предположение о виде законов распределения объектов. Если объекты каждого класса имеют многомерное нормальное распределение с одинаковой ковариационной матрицей S и векторами средних значений m_i, то пороговое значение w₀, минимизирующее критерий средней вероятности ошибки, будет

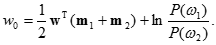
Для случая, когда число классов больше двух (K > 2), обычно определяется K дискриминантных векторов

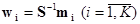
и пороговые величины

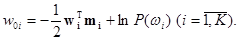
Объект x_k относится к классу w_i , если выполняется условие

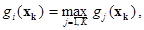
где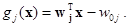

В формулы вычисления пороговых значений входят величины априорных вероятностей P(w_i). Априорная вероятность P(w_i) соответствует доле объектов, относящихся к классу w_i в большой серии наблюдений, проводящихся в некоторых стационарных условиях. Обычно P(w_i) неизвестны. Поэтому при решении практических задач, не меняя дискриминантных векторов, эти значения задаются на основании субъективных оценок исследователя. Также нередко полагают эти значения равными или пропорциональными объемам обучающих выборок из рассматриваемых диагностических классов.

Известны другие подходы к построению дискриминантных функций. Широко распространен классический вариант дискриминантного анализа, основанный на определении канонических направлений в исходном пространстве признаков, удовлетворяющих следующему критерию:

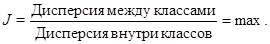
Весовой вектор w, удовлетворяющий данному критерию, исходя из геометрической интерпретации, задает новую координатную ось в исходном p‑мерном пространстве признаков y(x)=w^Tx (||w||=1) с максимальной неоднородностью исследуемой совокупности объектов. Новой оси соответствует, по существу, первая главная компонента объединенной совокупности объектов, полученная с учетом дополнительной обучающей информации о принадлежности объектов различным классам.

Дата добавления: 2021-03-18; просмотров: 74; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 123 4 Следующая ⇒

Мы поможем в написании ваших работ!