Прогнозирование поведения временного ряда
Предположим, что результатом некоторых наблюдений является временной ряд – информация о состоянии какого-то явления (например, курса доллара на торгах ММВБ) в разные моменты времени. Можно поставить задачу прогнозирования поведения временного ряда, то есть предсказания значения каких-то величин в будущие моменты времени. В этом направлении существуют два подхода.
В первом предполагается, что значение величины зависит главным образом от некоторых сторонних факторов и задача предсказания в этом случае сводится к выявлению зависимости прогнозируемой величины от других факторов. Для такого подхода удобно представлять временной ряд в естественном виде, то есть выбирать в качестве признаков время наблюдения, численное значение прогнозируемой величины, значения остальных факторов, предположительно имеющих отношение к делу.
Второй подход предполагает, что значение какой-либо величины можно предсказать, если знать ее поведение в прошлом. В этом случае изучаемый объект – это факт того, что прогнозируемая величина приняла определенное значение вместе с определенной предысторией изменения величины в прошлом.
Рассмотрим в качестве конкретного примера, как можно преобразовать простую таблицу изменения курса доллара для применения последнего из упомянутых подходов. В качестве признаков выберем значение самого курса, а также значения курса за последние n дней. Фрагмент данных приведен в табл. 3.7.
|
|
|
Таблица 3.7. Таблица для изучения изменения курса доллара
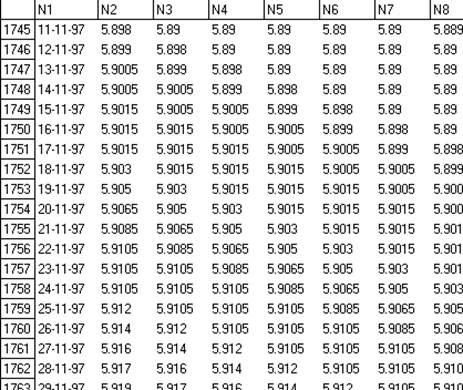
Таблица имеет характерный вид: значения признаков смещаются в каждой последующей строке на одну позицию вправо.
Геометрическая структура данных находит свое отражение в отношениях сходства (различия) между объектами и признаками. Сходство и различие объектов ТЭД определяется мерами близости (удаленности), а признаков – мерами связи. В зависимости от типа признаков (количественные, качественные, номинальные) применяются различные меры связи, которые будут рассмотрены ниже.
Меры связи между признаками
Матрица связи задает отношение "признак–признак" и представляет собой двумерную симметричную квадратную матрицу размера p ´ p
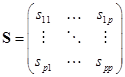 ,
,
где sij – мера связи между признаками xi и xj.
Известно большое количество мер связи между признаками. Они отличаются как объемом вычислений, так и теми аспектами связи, которые отражают. Различные авторы предлагают разные основания для классификации этих мер. Здесь будут рассмотрены две представительные группы связи между признаками /Статистические методы..., 1979/.
В первой группе используется принцип ковариации, а во второй – принцип сопряженности признаков. Исходя из первого принципа, заключение о наличии связи между переменными делается в том случае, когда увеличение значения одной переменной сопровождается устойчивым увеличением или уменьшением другой. Математически задача сводится к вычислению ковариации, то есть сопутствующего изменения численных значений признаков. Сюда относится в первую очередь коэффициент корреляции Пирсона (rkj), который представляет собой произведение моментов и является мерой линейной связи двух переменных xk и xj. Он вычисляется по формуле
|
|
|

где
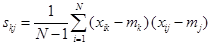
и

Многие меры связи отличаются от приведенного коэффициента корреляции Пирсона внешней стороной, но являются, по сути, алгебраическим преобразованием этого коэффициента, учитывающим тип сопоставляемых признаков. Так, например, коэффициент ранговой корреляции Спирмена (rs), часто применяемый для анализа порядковых признаков, представляет собой алгебраическое упрощение rkj. То же самое можно сказать о точечном бисериальном коэффициенте корреляции, который служит мерой связи между бинарной и количественной переменными. Некоторые другие коэффициенты, в частности тетрахорический коэффициент корреляции и бисериальный коэффициент корреляции, можно интерпретировать как аппроксимации rkj для определенных типов признаков /Гласс Дж., Стэнли Дж., 1975/.
|
|
|
Несколько иной подход в рассматриваемой группе мер связи основывается на подсчете числа несовпадений в ранжировке объектов по сопоставляемым переменным. Этот подход разработал М. Кендалл /Кендалл М., 1974/, когда предпринял попытку истолковать процесс измерения связи между переменными, не прибегая к принципу произведения моментов. Он рассмотрел два порядковых признака xi и xj, на каждый из которых N объектов отображаются в N последовательных рангов (1, 2, … , N). Из N объектов формируется N(N – 1)/2 пар, и для каждой пары подсчитывается количество совпадений порядка на признаке xi с порядком на признаке xj. Это количество обозначается "P". Таким же образом определяется количество несовпадений (инверсий) "Q". Коэффициент ранговой корреляции, получивший название "тау" Кендалла, вычисляется по формуле
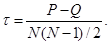
Несмотря на различие в подходах, между коэффициентами ранговой корреляции Спирмена и Кендалла, как отмечается в /Гласс Дж., Стэнли Дж., 1975/, существует тесная логическая связь. Вместе с тем, t Кендалла имеет интересную для математических статистиков интерпретацию: если из N объектов случайно выбираются два объекта, то разность между вероятностью того, что они будут иметь одинаковый порядок как по xi, так и по xj, и вероятностью того, что у них будет наблюдаться различие в порядках по xi и xj, равна величине t.
|
|
|
На основе подсчета количества совпадений и инверсий сконструирован целый ряд различных мер связи. В частности, этот принцип используется в коэффициенте ранговой корреляции Кертена и Гласса, который применяется для изучения взаимодействия дихотомической и порядковой переменной. В то же время Гласс /Glass G. V., 1966] показал, что данный коэффициент аналогичен бисериальному коэффициенту корреляции для порядковых переменных и для его вычисления можно обойтись без подсчета совпадений и инверсий.
Вторая обширная группа мер связи, основанная на принципе взаимной сопряженности, направлена на выяснение следующего факта: появляются ли некоторые значения одного признака одновременно с определенными значениями другого чаще, чем это можно объяснить случайным стечением обстоятельств. В данном случае фиксируется только сам факт наличия или отсутствия интересующих значений признака независимо от их количественного выражения /Никифоров А.М., Фазылов Ш.Х., 1988/. Общим, как бы переходным, для первой и второй групп мер связи является популярный в различных исследованиях коэффициент j, который предназначен для измерения связи двух дихотомических признаков или, иными словами, для анализа таблиц сопряженности 2´2.
Таблица 3.8. Таблица сопряженности дихотомических признаков
| Признак xj | Признак xi | Итог | |
| 0 | 1 | ||
| 1 | a | b | a + b |
| 0 | c | d | c + d |
| Итог | a + c | b + d | |
Коэффициент j представляет собой алгебраическое упрощение обычного коэффициента корреляции Пирсона rij с учетом специфики дихотомических признаков и вычисляется по формуле

Другие меры связи, основанные на принципе взаимной сопряженности, например коэффициенты Чупрова, Крамера, контингенции Пирсона и т. д., подробно рассматриваются в /Айвазян С.А. и др., 1983/.
В целом по проблеме выбора той или иной меры связи можно сказать следующее. Применение к одним и тем же данным различных мер связи нередко приводит к отличающимся результатам. Это обусловлено тем, что математики, конструировавшие коэффициенты корреляции, как правило, исследовали их свойства в предельных ситуациях – около 0 или 1. Поведение же различных мер связи внутри интервала [0, 1] сравнительно мало изучено. Поэтому на практике предпочтение какой либо мере связи бывает непросто обосновать, а результаты использования разных мер трудно сравнивать. Во многом выбор определяется личными симпатиями и интуицией исследователя. Рекомендации по применению тех или иных мер связи можно найти в [Дюк В.А., 1994]. Подробно все коэффициенты анализируются, например в /Гласс Дж., Стэнли Дж., 1975/.
Дата добавления: 2021-03-18; просмотров: 257; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
