Разложение функции, заданной на части промежутка
 .
.
До сих пор мы говорили о разложении в тригонометрический ряд функции, заданной на отрезке  . Рассмотрим теперь случай, когда
. Рассмотрим теперь случай, когда  задана лишь на части
задана лишь на части 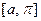 этого отрезка, где
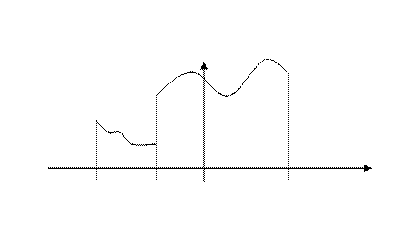
этого отрезка, где 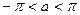 (рис. 4) Будем предполагать
(рис. 4) Будем предполагать  дифференцируемой на этом отрезке, и поставим вопрос о построении такого тригонометрического ряда
дифференцируемой на этом отрезке, и поставим вопрос о построении такого тригонометрического ряда
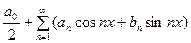 , (3)
, (3)
в который разлагалась бы функция  .
.
 |

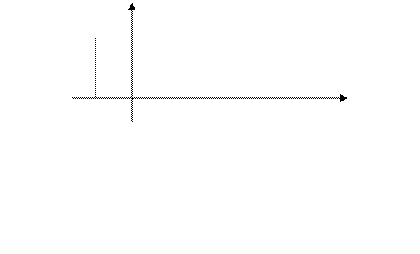
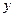
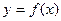
а 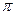

Рис. 4
Эту задачу можно решить так: выберем совсем произвольную функцию 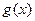 , заданную и дифференцируемую на отрезке
, заданную и дифференцируемую на отрезке 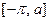 и определим на всём отрезке
и определим на всём отрезке  «составную» функцию
«составную» функцию 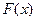 , положив
, положив
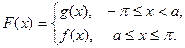
График 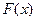 изображён на рис. 5.
изображён на рис. 5.
- 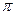 а
а 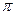

Рис. 5
Функция 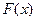 разлагается в свой ряд Фурье на всём отрезке
разлагается в свой ряд Фурье на всём отрезке  , за исключением может быть трёх точек
, за исключением может быть трёх точек 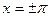 и
и 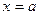 . В этих точках сумма ряда будет соответственно равна
. В этих точках сумма ряда будет соответственно равна
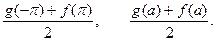
Поскольку, при 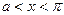 «составная функция
«составная функция 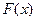 совпадает с
совпадает с  , то для этих х будет
, то для этих х будет
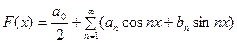 .
.
Если подбирать 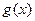 с условием
с условием 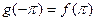 , то окажется
, то окажется 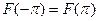 и равенство будет верно и при
и равенство будет верно и при 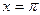 . Нако- нец, условие
. Нако- нец, условие 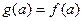 обеспечит справедливость равенства и при
обеспечит справедливость равенства и при 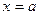
|
|
|
Таким образом, поставленная задача имеет решение. Однако это решение не единственно : ведь функцию 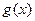 мы могли выбирать бесконечным множеством способов, а выбор этой функции определяет коэффициенты ряда.
мы могли выбирать бесконечным множеством способов, а выбор этой функции определяет коэффициенты ряда.
Например, 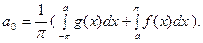
Поэтому (в отличие от функции, заданной на всём отрезке  ) функция, заданная на более коротком отрезке, допускает бесконечное множество представлений вида (3). Здесь не имеет место теорема о единственности.
) функция, заданная на более коротком отрезке, допускает бесконечное множество представлений вида (3). Здесь не имеет место теорема о единственности.
Всё сказанное о 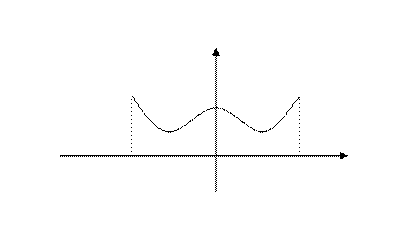 тносится, в частности, и к отрезку
тносится, в частности, и к отрезку  . Но тут появляется некое новое обстоятельство. Именно, если мы захотим, взять
. Но тут появляется некое новое обстоятельство. Именно, если мы захотим, взять  такой, чтобы «составная функция»
такой, чтобы «составная функция» 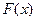 оказалась чётной (рис. 9).
оказалась чётной (рис. 9).
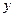
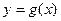
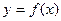
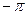 О
О 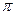

Рис. 6
Это приводит к разложению
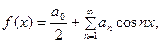 , (4)
, (4)
в котором
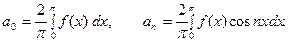 . (5)
. (5)
Нетрудно видеть, что формула (4) верна на всём отрезке 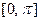 .
.
С другой стороны, мы можем выбрать 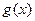 и так, чтобы функция
и так, чтобы функция 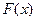 оказалась нечётной (рис. 7). Это приведёт нас к разложению
оказалась нечётной (рис. 7). Это приведёт нас к разложению
|
|
|
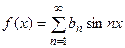 , (6)
, (6)
в котором
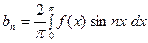 . (7)
. (7)
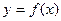
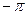 О
О 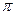

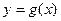
Рис. 7
Формула (6) верна при 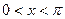 . Чтобы она была верна при
. Чтобы она была верна при 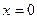 , необходимо, чтобы было
, необходимо, чтобы было 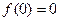 , так как правая часть равенства (6) обращается в ноль при
, так как правая часть равенства (6) обращается в ноль при 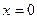 . Точно также для справедливости формулы (6) в точке
. Точно также для справедливости формулы (6) в точке 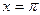 необходимо, чтобы было
необходимо, чтобы было 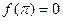 .
.
Таким образом, имеет место.
ТЕОРЕМА 1. Функцию  , заданную и дифференцируе - мую на отрезке
, заданную и дифференцируе - мую на отрезке 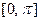 можно бесконечным множеством спо- собов разложить в тригонометрический ряд. В частности, её можно разложить по косинусам в ряд (4), коэффициенты которого определяются формулами (5), или в ряд по синусам (6) с коэффициентами (7).
можно бесконечным множеством спо- собов разложить в тригонометрический ряд. В частности, её можно разложить по косинусам в ряд (4), коэффициенты которого определяются формулами (5), или в ряд по синусам (6) с коэффициентами (7).
ПРИМЕРЫ. 1). Пусть 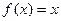 . Разложить эту функцию в ряд по косинусам
. Разложить эту функцию в ряд по косинусам
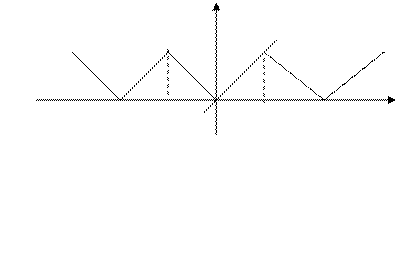
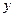
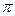
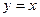
|
|
|

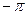 О
О 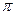

Рис. 8
Здесь
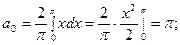
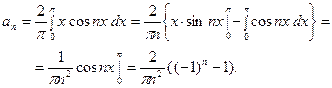
Отсюда, при 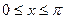 будет
будет
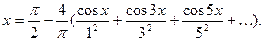 (8)
(8)
В частности, при 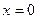 мы снова находим
мы снова находим
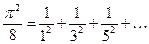
Сумма ряда (8) является 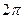 - периодической и чётной функцией. Её график изображён на рис. 8.
- периодической и чётной функцией. Её график изображён на рис. 8.
2). Пусть функция 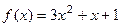 , заданная на
, заданная на 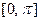 , разложена в тригонометрический ряд по синусам. Найти сумму ряда
, разложена в тригонометрический ряд по синусам. Найти сумму ряда 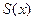 в точках
в точках
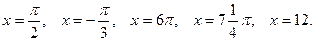
Решение. а) Так как 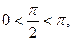 то
то
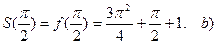 Так как
Так как 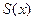 нечётная, то
нечётная, то
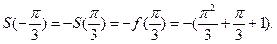 с)
с) 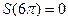 ,
,
так как при 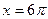 все члены ряда обращаются в ноль
все члены ряда обращаются в ноль 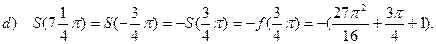
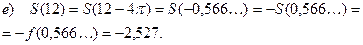
Сдвиг основного промежутка.
Всю теорию рядов Фурье мы излагали для функций, заданных на отрезке 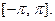 Однако вместо этого отрезка можно было бы положить в основу любой другой отрезок длины
Однако вместо этого отрезка можно было бы положить в основу любой другой отрезок длины 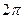 . Дело в том, что это период всех функций сис- темы :
. Дело в том, что это период всех функций сис- темы :
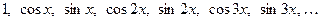 (9) и справедлива
(9) и справедлива
ТЕОРЕМА 2. Если функция 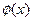 имеет период равный
имеет период равный 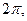 то интеграл
то интеграл 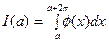 не зависит от числа а.
не зависит от числа а.
В самом деле,
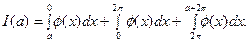 (10)
(10)
В последнем интеграле справа можно сделать замену 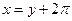 , дающую
, дающую
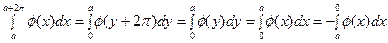
Таким образом, первый и третий интегралы правой части (10) взаимно уничтожаются и
|
|
|
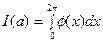 ,
,
чем и доказана теорема.
В частности, из неё следует, что 1) любые две функции системы (9) взаимно ортогональны на всяком отрезке длины 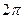 и 2) при всяком
и 2) при всяком 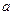 будет
будет
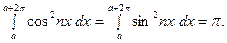
Следовательно, всю теорию можно перенести с отрезка  на любой отрезок
на любой отрезок 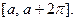 Например, верна:
Например, верна:
ТЕОРЕМА 3. Если функция  дифференцируема на от- резке
дифференцируема на от- резке 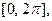 то всюду на открытом промежутке
то всюду на открытом промежутке 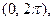 будет
будет
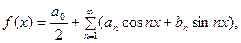 (11)
(11)
где
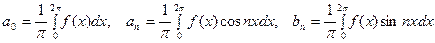
Ряд (11) сходится и в точках 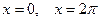 , где его сум -ма равна
, где его сум -ма равна
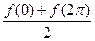 .
.
ПРИМЕР. Разложить в ряд Фурье функцию 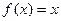 , рассматриваемую на отрезке
, рассматриваемую на отрезке 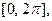
Здесь
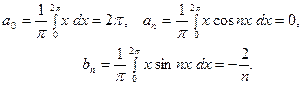
Следовательно, при 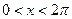 будет
будет
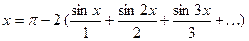 . (12)
. (12)
В частности, при 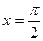 получаем уже знакомое равенство
получаем уже знакомое равенство
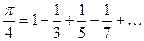
В точках 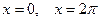 сумма
сумма 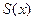 ряда (12) равна
ряда (12) равна 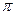 .
.
Нетрудно понять, что 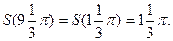
§ 4. РЯД ФУРЬЕ ДЛЯ ФУНКЦИИ С ПРОИЗВОЛЬНЫМ
ПЕРИОДОМ.
Мы видели, что ряды вида
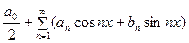 (1)
(1)
являются хорошим аналитическим аппаратом для представ- ления функций, заданных на промежутке длины 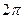 .
.
Рассмотрим теперь функции 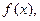 заданные на отрезке длины
заданные на отрезке длины 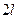 . Пусть для определённости речь идёт о функции
. Пусть для определённости речь идёт о функции 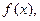 заданной и дифференцируемой на отрезке
заданной и дифференцируемой на отрезке 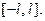 По- ложим
По- ложим
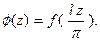
Тогда 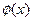 будет заданной и дифференцируемой уже на отрезке
будет заданной и дифференцируемой уже на отрезке 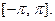 Значит, к
Значит, к 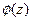 применима теория, изложен -ная выше, и потому при
применима теория, изложен -ная выше, и потому при 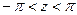 будет
будет
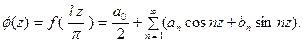
Положим в этом равенстве 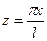 .
.
Тогда для 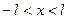 получаем равенство
получаем равенство
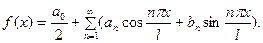 . (2)
. (2)
В точках 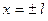 сумма ряда равна
сумма ряда равна
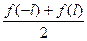 .
.
Остановимся на коэффициентах ряда (2). Например,
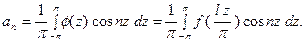 .
.
Подстановка 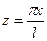 даёт
даёт
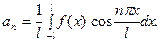
Аналогично,
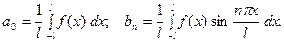
Что касается функций, заданных и дифференцируемых на отрезке 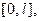 то они допускают бесчисленное множество разложений вида (2). В частности, их можно разлагать по косинусам и по синусам. Последнее разложение имеет вид
то они допускают бесчисленное множество разложений вида (2). В частности, их можно разлагать по косинусам и по синусам. Последнее разложение имеет вид
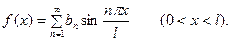 ,
,
где
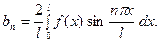 (3)
(3)
ПРИМЕРЫ.
1. Найти разложение в ряд Фурье функции:
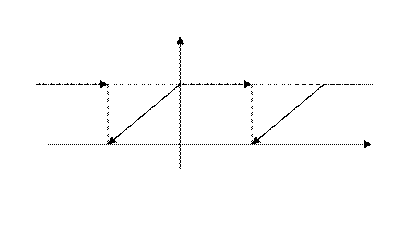
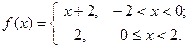

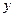
2
-2 0 2  Рис. 9
Рис. 9
Найдём коэффициенты Фурье. 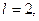 тогда
тогда
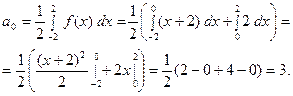
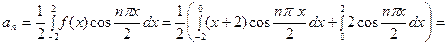 Для первого интеграла применим формулу интегрирования по частям;
Для первого интеграла применим формулу интегрирования по частям;
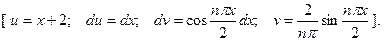
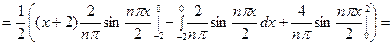

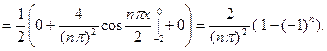
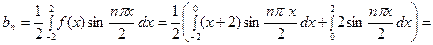 Для первого интеграла применим формулу интегрирования
Для первого интеграла применим формулу интегрирования
по частям;
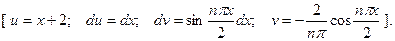
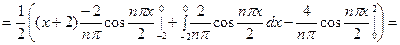
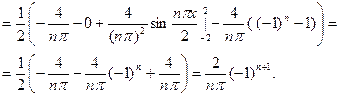
Следовательно, на промежутке 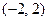 ряд Фурье имеет вид
ряд Фурье имеет вид
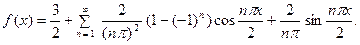
2. Найти ряд Фурье для чётной функции:
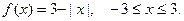
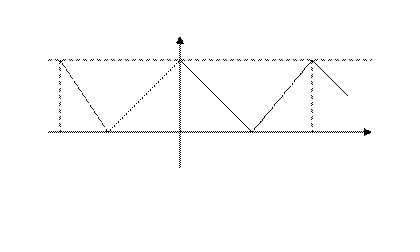
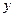
3
-3 0 3 6 
Рис. 10
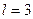 , функция чётная, поэтому
, функция чётная, поэтому 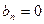 . Найдём остальные коэффициенты ряда, учитывая, что при
. Найдём остальные коэффициенты ряда, учитывая, что при 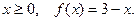
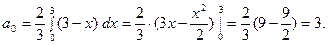
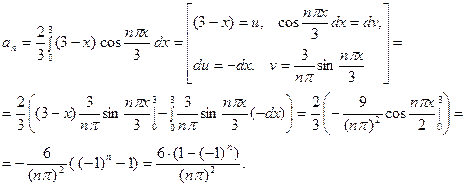 Тогда получаем:
Тогда получаем:
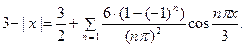
3. Разложить функцию 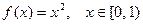 в неполный ряд Фурье по
в неполный ряд Фурье по 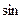 .
.
Дополним график функции нечётным образом.
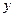
1
-2 -1 0 1 2 
-1
Рис. 11
В данном примере 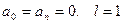 . Коэффициенты
. Коэффициенты 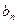
находим по формуле:
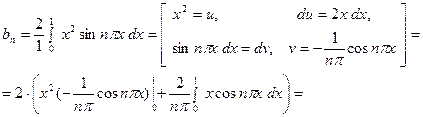
Второй интеграл снова интегрируем по частям:
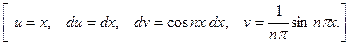
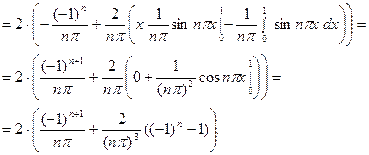
Тогда: 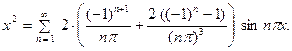
§ 5 РЯД ФУРЬЕ В КОМПЛЕКСНОЙ ФОРМЕ.
Пусть дан ряд Фурье для функции  на отрезке
на отрезке 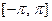 :
:
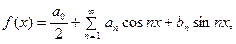 (1) с коэффициентами
(1) с коэффициентами
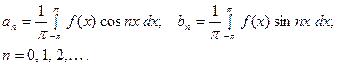 (2)
(2)
Обратимся к формуле Эйлера:
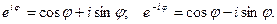
Отсюда
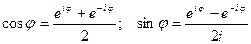 . (3)
. (3)
Используя формулы (3), получаем;
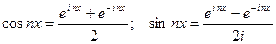 .
.
Подставим данные выражения в ряд (1)
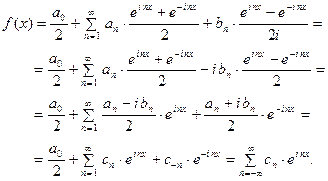
Полученный ряд и является рядом Фурье в комплексной форме. При этом коэффициенты данного ряда вычисляются по формулам:
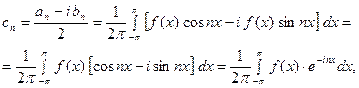
аналогично,
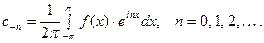
Такие же формулы можно получить, преобразовав ряд Фурье для случая произвольного промежутка 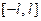 :
:
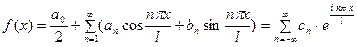 , (4) где
, (4) где
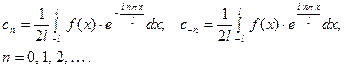
Или 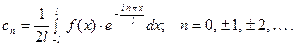
Очевидно, что ряд Фурье в комплексной форме имеет более компактный вид.
В электротехнике и радиотехнике элементы ряда Фурье в комплексной форме
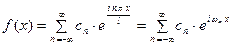
называются гармониками, коэффициенты 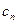 - комплексными амплитудами,
- комплексными амплитудами, 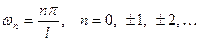 - волновыми числами функции
- волновыми числами функции  .
.
ПРИМЕР. Построить ряд Фурье в комплексной форме для функции:
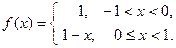
Для данной функции 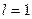 .
.
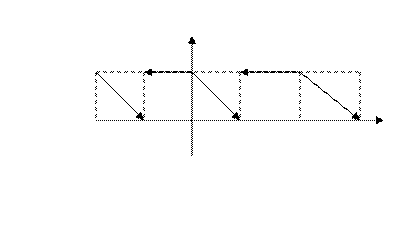
1
-2 -1 0 1 2 3 
Рис. 12
При  ,
,
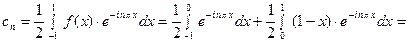
для второго интеграла
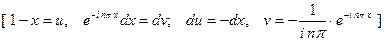
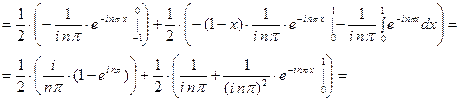
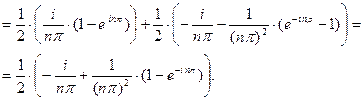
При 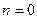
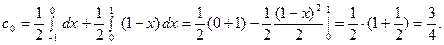
Следовательно, для всех точек непрерывности функции  имеет место равенство:
имеет место равенство:
§ 6. ПРИЛОЖЕНИЯ РЯДОВ ФУРЬЕ.
Задача о колебании струны.
Ряды Фурье находят многочисленные применения. Здесь мы покажем, как они используются при решении задачи о колебании струны. Струной называется гибкая нить, не оказывающая сопротивления изгибу.
Рассмотрим струну, которая в начальный момент совмещена с отрезком 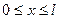 оси Ох. Мы будем считать, что концы струны
оси Ох. Мы будем считать, что концы струны 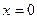 и
и 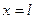 закреплены на оси Ох. Пусть струна растягивается силами
закреплены на оси Ох. Пусть струна растягивается силами 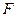 и
и 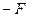 , приложенными к её концам в направлении вдоль оси Ох. Если струну вывести из состояния равновесия и затем предоставить себе самой, то под влиянием растягивающих сил точки струны придут в движение, стремясь вернуться в исходное положение. Однако, придя в это положение, каждая точка струны будет обладать уже некоторой скоростью и по инерции пройдёт дальше своего равновесного положения. При этом дальнейшем движении точек они будут тормозиться растягивающими силами и т.д. Таким образом, струна будет совершать некоторое колебательное движение. Задача состоит в исследовании этого движения.
, приложенными к её концам в направлении вдоль оси Ох. Если струну вывести из состояния равновесия и затем предоставить себе самой, то под влиянием растягивающих сил точки струны придут в движение, стремясь вернуться в исходное положение. Однако, придя в это положение, каждая точка струны будет обладать уже некоторой скоростью и по инерции пройдёт дальше своего равновесного положения. При этом дальнейшем движении точек они будут тормозиться растягивающими силами и т.д. Таким образом, струна будет совершать некоторое колебательное движение. Задача состоит в исследовании этого движения.
Сделаем ряд предположений. Прежде всего, мы считаем, что, выводя струну из состояния равновесия, мы придаём ей форму некоторой линии 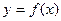 , лежащей на плоскости хОу и не сообщаем точкам струны никаких начальных скоростей. Тогда во всё время движения струна будет находиться в плоскости хОу. Мы будем предполагать, что каждая точка струны совершает только поперечные колебания, перпендикулярные оси Ох. Это колебание мы предположим столь малым, что квадратами отклонений точек струны от оси Ох можно пренебречь. Кроме того, будем считать, что во всё время движения струна будет сохранять пологую форму. Это означает, что угол
, лежащей на плоскости хОу и не сообщаем точкам струны никаких начальных скоростей. Тогда во всё время движения струна будет находиться в плоскости хОу. Мы будем предполагать, что каждая точка струны совершает только поперечные колебания, перпендикулярные оси Ох. Это колебание мы предположим столь малым, что квадратами отклонений точек струны от оси Ох можно пренебречь. Кроме того, будем считать, что во всё время движения струна будет сохранять пологую форму. Это означает, что угол 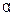 образуемый касательной к струне с осью Ох, достаточно мал, чтобы можно было считать
образуемый касательной к струне с осью Ох, достаточно мал, чтобы можно было считать
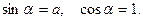 (1)
(1)
Наконец, мы считаем струну однородной, причём массу единицы длины струны в её нерастянутом состоянии обозначим 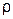 .
.
Возьмём какую - либо точку струны, имеющую в начальный момент 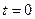 абсциссу
абсциссу 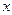 . Так как эта точка будет двигаться перпендикулярно оси Ох, то во время движения её абсцисса
. Так как эта точка будет двигаться перпендикулярно оси Ох, то во время движения её абсцисса 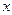 не будет меняться. Однако же её
не будет меняться. Однако же её 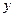 будет зависеть от времени, а также от того, о какой точке идёт речь, т.е. от абсциссы
будет зависеть от времени, а также от того, о какой точке идёт речь, т.е. от абсциссы 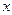 этой точки. Таким образом, эта ордината является функцией от
этой точки. Таким образом, эта ордината является функцией от 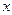 и от времени
и от времени 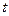 . Эту функцию мы будем обозначать через
. Эту функцию мы будем обозначать через 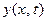 . Итак, дело сводится к нахождению функции
. Итак, дело сводится к нахождению функции 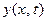 . Ясно, что эта неизвестная функция должна удовлетворять граничным условиям
. Ясно, что эта неизвестная функция должна удовлетворять граничным условиям
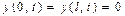 , (2)
, (2)
выражающим то, что концы струны 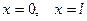 в любой момент времени находятся на оси Ох, и удовлетворяют начальным условиям
в любой момент времени находятся на оси Ох, и удовлетворяют начальным условиям
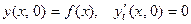 , (3)
, (3)
первое из которых выражает то, что в начальный момент 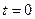 струне придана заданная форма
струне придана заданная форма 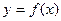 , а второе означает, что точки струны не имеют начальных скоростей.
, а второе означает, что точки струны не имеют начальных скоростей.
Выведем теперь дифференциальное уравнение, которому должна удовлетворять неизвестная функция 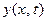 . Для этого выделим из струны элементарный отрезок, который в начальный момент
. Для этого выделим из струны элементарный отрезок, который в начальный момент 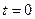 совпадает с отрезком
совпадает с отрезком 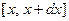 оси Ох. В момент
оси Ох. В момент 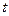 этот отрезок представляет собой элементарную дугу линии
этот отрезок представляет собой элементарную дугу линии 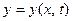 . Длина этой дуги равна
. Длина этой дуги равна
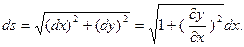
Пренебрегая членом 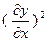 , (это основано в предпо- ложении пологой формы струныж однако,
, (это основано в предпо- ложении пологой формы струныж однако, 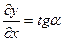 и значит,
и значит, 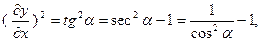 а мы считаем, что
а мы считаем, что 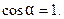 ) получим
) получим 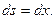
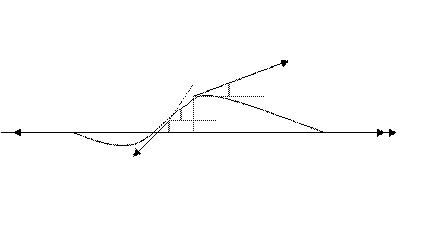 Масса выделенного элемента равна
Масса выделенного элемента равна 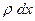 . К этому эле -менту будут приложены растягивающие его силы. Пусть натя- жение струны в точке
. К этому эле -менту будут приложены растягивающие его силы. Пусть натя- жение струны в точке  будет равно
будет равно 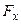 .
.
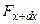
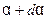
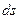
0 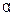
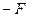

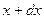
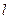
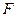 х
х
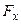
Рис. 13
Тогда к концам нашего элемента будут приложены силы 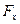 и
и 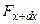 . Они направлены по касательным, проведённым к струне в точках
. Они направлены по касательным, проведённым к струне в точках  и
и 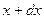 . Обозначим через
. Обозначим через 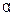 угол между осью Ох и касательной к струне в точке
угол между осью Ох и касательной к струне в точке  . В точке
. В точке 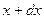 этот угол пусть будет равен
этот угол пусть будет равен 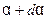 (Рис. 13).
(Рис. 13).
Обозначим равнодействующую сил, приложенных к концам элемента, через 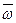 . Тогда векторное уравнение движения эле- мента имеет вид
. Тогда векторное уравнение движения эле- мента имеет вид
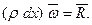 (4)
(4)
Проектируя это уравнение на ось Ох, находим
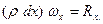 (5)
(5)
(Предостерегаем от недоразумений: символ 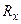 означает проекцию силы
означает проекцию силы 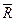 на ось Ох, а
на ось Ох, а 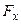 - численное значение натяжения в точке
- численное значение натяжения в точке  ).
).
Поскольку точки струны движутся перпендикулярно оси Ох, то 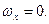 Стало быть и
Стало быть и 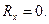 Но
Но
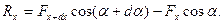
В силу (1), будет 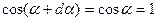 и потому
и потому 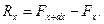 Сопоставляя это с равенством
Сопоставляя это с равенством 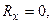 нахо -дим, что
нахо -дим, что 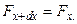 Это значит, что величина натяжения струны не меняется вдоль струны. Поскольку же на концах струны это натяжение равно
Это значит, что величина натяжения струны не меняется вдоль струны. Поскольку же на концах струны это натяжение равно 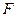 , то и во всех точках струны оно равно
, то и во всех точках струны оно равно 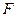 , и, вместо
, и, вместо 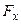 и
и 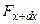 , можно писать
, можно писать 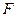 . Спроектируем теперь уравнение (4) на ось Оу
. Спроектируем теперь уравнение (4) на ось Оу
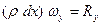 . (6)
. (6)
Так как 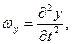 а (см. (1))
а (см. (1))
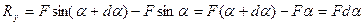 ,
,
то (6) даёт
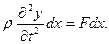 .
.
( 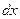 означает приращение угла
означает приращение угла 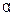 , когда в закреплённый мо- мент времени
, когда в закреплённый мо- мент времени 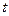 абсцисса
абсцисса  получает приращение
получает приращение 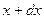 . Поэтому отношение
. Поэтому отношение 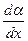 есть, строго говоря, частная произ- водная
есть, строго говоря, частная произ- водная 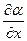 ). Или
). Или
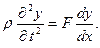 (7)
(7)
Вспомним теперь, что 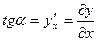 . Отсюда
. Отсюда
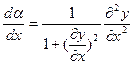 .
.
Как и выше, членом 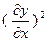 можно пренебречь, откуда
можно пренебречь, откуда
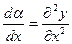 .
.
Положив для краткости 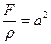 , приводим уравнение (7) к виду
, приводим уравнение (7) к виду
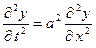 . (8)
. (8)
Это знаменитое уравнение колебания струны. Мы видим, что это дифференциальное уравнение с частными произ -водными. Такие уравнения до сих пор мы ещё не изучали.
Таким образом, наша механическая задача свелась к чисто математической: найти такое решение уравнения (8), которое удовлетворяет условиям (2) и (3).
Существуют разные способы решить задачу, к которой мы пришли.
Один из способов был предложен в 18 веке Д. Бернулли. Позже, уже в 19 веке, этот способ систематически применялся Фурье для решения целого ряда термодинамических задач, почему он и получил название метода Фурье. Этот способ мы и изложим. Он заключается в том, что сначала решается следующая задача.
Вспомогательная задача: Найти функцию 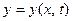 , удовлетворяющую требованиям:
, удовлетворяющую требованиям:
1) 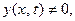 тождественно, ( 9)
тождественно, ( 9)
2) 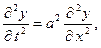 (10)
(10)
3) 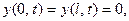 (11)
(11)
4) 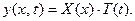 (12)
(12)
Отличие вспомогательной задачи от той, которую нам на самом деле нужно решить, состоит в том, что от искомой функции 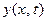 мы уже не требуем, чтобы она удо- влетворяла начальным условиям (3), но зато требуем, чтобы она имела специальный вид
мы уже не требуем, чтобы она удо- влетворяла начальным условиям (3), но зато требуем, чтобы она имела специальный вид 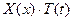 , т.е. представлялась в виде произведения функции
, т.е. представлялась в виде произведения функции 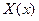 от одного только
от одного только  на функцию
на функцию 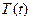 одного только
одного только 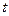 . Кроме того, мы налагаем на функцию
. Кроме того, мы налагаем на функцию 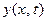 естественное условие, а именно она не должна быть тождественным нулём.
естественное условие, а именно она не должна быть тождественным нулём.
Оказывается, что изменённая таким образом задача, решается довольно легко и что она имеет бесконечное множество решений, из которых удаётся составить и решение нашей основной задачи.
Займёмся же поставленной вспомогательной задачей.
Из (9) вытекает существование такой точки 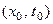 , что
, что 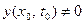 . Тогда
. Тогда 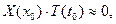 т.е.
т.е. 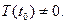 Подста -вим значение
Подста -вим значение 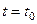 в граничные условия (11):
в граничные условия (11):
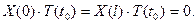
Отсюда видно, что искомая функция 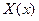 должна удовле- творять условиям:
должна удовле- творять условиям:
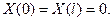 (13)
(13)
Подставляя (12) в (10) получим
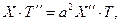
т.е.
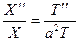 . (14)
. (14)
Но (внимание!) правая часть равенства (14) не зависит от  . Значит и левая часть (14) от
. Значит и левая часть (14) от  не должна зависеть. С другой стороны, эта левая часть может быть функцией только одного
не должна зависеть. С другой стороны, эта левая часть может быть функцией только одного  , так как
, так как 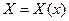 . Значит, левая (а с ней и пра- вая) часть равенства должна быть постоянной величиной. Обозначим эту (неизвестную нам) постоянную через
. Значит, левая (а с ней и пра- вая) часть равенства должна быть постоянной величиной. Обозначим эту (неизвестную нам) постоянную через 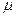 .
.
Допустим сначала, что 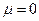 . Тогда из (14) следует,
. Тогда из (14) следует,
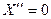 .
.
Отсюда 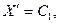 и
и 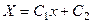 , т.е.,
, т.е., 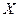 должна быть линейной функцией. Подставляя найденное значение
должна быть линейной функцией. Подставляя найденное значение 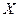 в условие (13), получим
в условие (13), получим 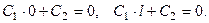 Но тогда
Но тогда 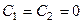 , т.е.
, т.е. 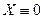 , а с ним и
, а с ним и 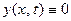 , что проти- воречит (9). Таким образом, не существует решения вспомо -гательной задачи, у которой было бы
, что проти- воречит (9). Таким образом, не существует решения вспомо -гательной задачи, у которой было бы 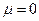 .
.
Допустим теперь, что 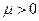 , т.е. что
, т.е. что 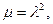 где
где 
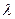 мож -но считать положительным. Тогда
мож -но считать положительным. Тогда
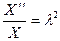 , т.е.
, т.е. 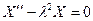 .
.
Общее решение этого линейного уравнения имеет вид
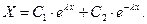
Подставляя найденное значение 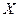 в (13), получим
в (13), получим
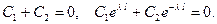
Решая эту систему, находим 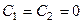 . Это снова приводит к соотношению
. Это снова приводит к соотношению 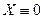 , противоречащему условию (9). Итак, неравенство
, противоречащему условию (9). Итак, неравенство 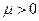 тоже оказывается невозможным. Стало быть, вспомогательную задачу можно рассматривать, только предполагая, что неизвестное
тоже оказывается невозможным. Стало быть, вспомогательную задачу можно рассматривать, только предполагая, что неизвестное 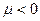 , т.е., что
, т.е., что 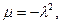 где
где 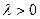 . Таким образом,
. Таким образом,
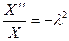 или
или 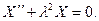
Решение этого уравнения есть
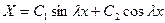
Первое из граничных условий (13) даёт 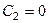 . Значит (заменяя
. Значит (заменяя 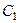 , на
, на 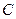 ),
),
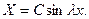
Если бы было 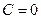 , то мы не пришли бы к решению нашей вспомогательной задачи, ибо получилось бы проти- воречие с (9). Стало быть
, то мы не пришли бы к решению нашей вспомогательной задачи, ибо получилось бы проти- воречие с (9). Стало быть 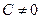 . Но тогда второе из условий (13) даёт
. Но тогда второе из условий (13) даёт 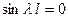 . Это возможно лишь при
. Это возможно лишь при
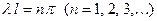 .
.
Значит для 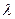 возможны лишь значения
возможны лишь значения
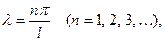
что приводит к следующим выражениям для 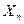 :
:
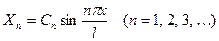 ,
,
причём 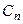 при каждом
при каждом  может принять любое (отличное от 0) значение.
может принять любое (отличное от 0) значение.
Выберем какое-либо из возможных значений 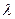 и подста -вим в (14):
и подста -вим в (14):
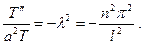
Отсюда
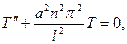
т.е.
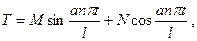
где 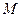 и
и 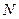 - произвольные постоянные. Обозначая Это
- произвольные постоянные. Обозначая Это 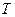 через
через 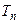 и полагая
и полагая 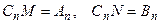 получаем бесконечное множество решений вспомогательной задачи
получаем бесконечное множество решений вспомогательной задачи
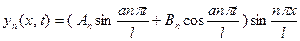 . (15)
. (15)
Здесь 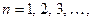 а
а 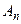 и
и 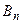 - произвольные постоянные.
- произвольные постоянные.
Любая функция (15) удовлетворяет уравнению (10) и граничным условиям (11), причём это верно уже и без ограничений 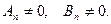
Заметим теперь, что и уравнение (10) и условия (11) линейны и однородны, т.е. таковы, что сумма функций, удовлетворяющих им, также будет удовлетворять и уравнению и граничным условиям. Поэтому функция
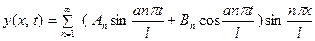 (16)
(16)
при условии сходимости выписанного ряда, также будет удо-влетворять уравнению (10) и граничным условиям (11). Отме- тим, что 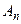 и
и 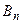 остаются при этом произвольными посто- янными (при условии, что не нарушается сходимость получен- ного ряда). Чтобы функция (16) была решением интересующей нас (уже не вспомогательной, а основной) задачи, нужно подо- брать
остаются при этом произвольными посто- янными (при условии, что не нарушается сходимость получен- ного ряда). Чтобы функция (16) была решением интересующей нас (уже не вспомогательной, а основной) задачи, нужно подо- брать 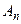 и
и 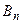 так, чтобы выполнялись начальные условия (3).
так, чтобы выполнялись начальные условия (3).
Первое условие (3) даёт
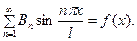 (17)
(17)
Дифференцируя (16), получим
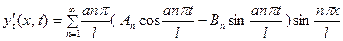 .
.
Полагая 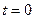 и учитывая второе из условий (3), получим
и учитывая второе из условий (3), получим
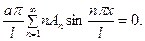 (18)
(18)
Чтобы удовлетворить соотношение (18) нужно принять, 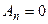 (
( 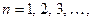 ) Соотношение же (17) показывает, что коэффициенты
) Соотношение же (17) показывает, что коэффициенты 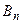 должны быть коэффициентами разложения функции
должны быть коэффициентами разложения функции  , заданной на
, заданной на 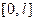 по функциям
по функциям 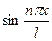 , т.е
, т.е
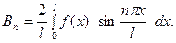 (19)
(19)
Сдедовательно, искомое решение имеет вид
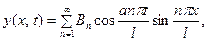
где 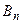 определяется из (19).
определяется из (19).
ПРИМЕР. Пусть 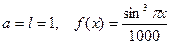 . Найти
. Найти 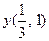 .
.
Решение. Найдём сначала разложение (17). Это гораздо проще сделать без использования формул (19), непосредст- венно. Действительно,
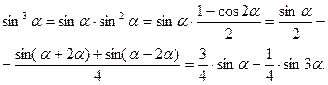
Значит, 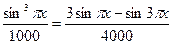 ,
,
откуда 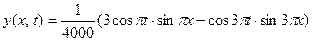
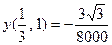 .
.
2 Распространение тепла в стержне.
В качестве другого применения рядов Фурье рассмотрим задачу о распространении тепла в стержне. Пусть стержень длины 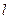 весь, кроме своих концов , помещён в теплоизо -лирующую оболочку и нагрет до некоторой температуры, различной в различных его точках. Если этот стержень пре- доставить самому себе, то заключённое в нём тепло будет перетекать от более нагретых точек к менее нагретым, и температура стержня с течением времени станет вырав- ниваться, причём на этот процесс будет влиять также и режим, который поддерживается на концах стержня. Задача состоит в том, чтобы, зная упомянутый режим, и распреде- ление температур вдоль стержня в начальный момент
весь, кроме своих концов , помещён в теплоизо -лирующую оболочку и нагрет до некоторой температуры, различной в различных его точках. Если этот стержень пре- доставить самому себе, то заключённое в нём тепло будет перетекать от более нагретых точек к менее нагретым, и температура стержня с течением времени станет вырав- ниваться, причём на этот процесс будет влиять также и режим, который поддерживается на концах стержня. Задача состоит в том, чтобы, зная упомянутый режим, и распреде- ление температур вдоль стержня в начальный момент 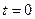 , найти это распределение в последующие моменты
, найти это распределение в последующие моменты 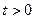 . Для этого естественно надо задать и термические характеристики стержня:: его теплоёмкость
. Для этого естественно надо задать и термические характеристики стержня:: его теплоёмкость 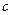 и коэффициент теплопровод- ности
и коэффициент теплопровод- ности 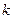 . Напомним, что
. Напомним, что 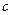 - это количество калорий, которое нужно подать, чтобы единицу массы стержня (мы считаем его однородным с линейной плотностью
- это количество калорий, которое нужно подать, чтобы единицу массы стержня (мы считаем его однородным с линейной плотностью 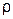 нагреть на
нагреть на 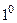 . Коэф- фициент
. Коэф- фициент 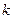 представляет собой количество тепла ( в калори -ях), которое будет протекать за единицу времени через сечение стержня, если температура стержня падает на
представляет собой количество тепла ( в калори -ях), которое будет протекать за единицу времени через сечение стержня, если температура стержня падает на 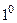 при перемещении вдоль стержня на единицу длины. Мы будем обозначать температуру стержня в точке
при перемещении вдоль стержня на единицу длины. Мы будем обозначать температуру стержня в точке  (один из концов стержня (назовём его «левым») фиксируется и точкой
(один из концов стержня (назовём его «левым») фиксируется и точкой  называется точка, отстоящая от этого конца на расстояние
называется точка, отстоящая от этого конца на расстояние  ) в момент времени
) в момент времени 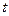 через
через 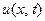 . Это и есть та вели- чина, которую нужно найти. Температуру же
. Это и есть та вели- чина, которую нужно найти. Температуру же 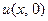 стержня в начальный момент мы считаем известной и обозначаем через
стержня в начальный момент мы считаем известной и обозначаем через 
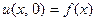 . (20)
. (20)
Что касается температурного режима на концах стержня, этот режим может быть весьма разнообразен. Можно, напри -мер, на концах отрезка поддерживать температуру, изменяю- щуюся по заданным законам 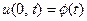 ,
, 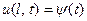 и т.п.), то мы рассмотрим два случая:
и т.п.), то мы рассмотрим два случая:
А) концы погружены в тающий лёд, т.е. в них поддержи- вается постоянная температура
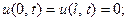 (21)
(21)
В) концы погружены в ту же теплоизолирующую оболочку, что и весь стержень. Это означает, что через концы не про -исходит протекание тепла. Математическое выражение этой за- кономерности мы найдём несколько позже.
Рассмотрим сечение  нашего стержня и найдём какое ко- личество
нашего стержня и найдём какое ко- личество 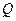 тепла протечёт (слева направо) через это сече- ние за элементарный промежуток времени
тепла протечёт (слева направо) через это сече- ние за элементарный промежуток времени 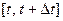 . В мо -мент
. В мо -мент 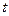 температура стержня в точке
температура стержня в точке  будет равна
будет равна 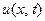 .
.
Возьмём отличную от  точку
точку 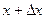 стержня. Пусть, для определённости,
стержня. Пусть, для определённости, 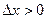 , т.е. новая точка лежит правее ста -рой. В ней температура стержня в момент
, т.е. новая точка лежит правее ста -рой. В ней температура стержня в момент 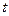 будет равна
будет равна 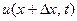 . Таким образом, падение температуры при пере- мещении из
. Таким образом, падение температуры при пере- мещении из  в
в 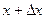 оказывается равным
оказывается равным
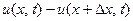 .
.
Следлвательно, на единицу длины стержня (на участке 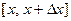 ) приходится падение температуры, равное
) приходится падение температуры, равное
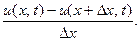
Если 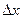 весьма мало, то найденную величину можно при -нять за
весьма мало, то найденную величину можно при -нять за 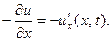 Такое падение температуры застави- ло бы за единицу времени перейти сечение
Такое падение температуры застави- ло бы за единицу времени перейти сечение  количество тепла, равное
количество тепла, равное 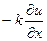 калорий. За время же
калорий. За время же 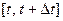 через наше сечение перейдёт (слева направо)
через наше сечение перейдёт (слева направо)
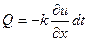 (22)
(22)
калорий.. (Если 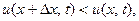 то температура падает при перемещении слева направо. В этом случае тепло поте -чёт через сечение
то температура падает при перемещении слева направо. В этом случае тепло поте -чёт через сечение  также слева направо, т.е. окажется
также слева направо, т.е. окажется 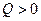 . Это вполне согласуется с тем, что в нашем случае
. Это вполне согласуется с тем, что в нашем случае 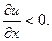 Если же
Если же 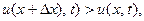 то тепло потечёт справа налево, т.е. будет
то тепло потечёт справа налево, т.е. будет 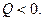 Но тогда
Но тогда 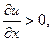 и форму- ла (22) снова будет справедливой.)
и форму- ла (22) снова будет справедливой.)
Если концы стержня теплоизолированы, то количество тепла, протекающее через них, равно 0, и потому
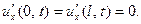 (23)
(23)
Это и есть то выражение режима 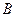 , о котором мы упомя -нули выше.
, о котором мы упомя -нули выше.
Выделим из нашего стержня элементарный отрезок 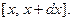 За время
За время 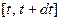 через сечение
через сечение  в наш отре- зок войдёт (из расположенной левее
в наш отре- зок войдёт (из расположенной левее  части стержня)
части стержня)
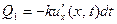
калорий. За это же время из нашего отрезка через его конец 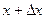 уйдёт направо
уйдёт направо
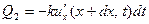
калорий. Стало быть, в рассматриваемом отрезке за время 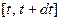 накопится количество тепла, равное
накопится количество тепла, равное
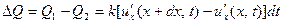
калорий. Поскольку малое приращение функции можно заме -ить её дифференциалом, то
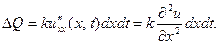
Подача такого количества тепла должна повысить темпе -ратуру единицы массы стержня на
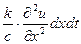
градусов. Поскольку же масса отрезка 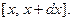 равна
равна 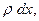 то соответствующее повышение температуры будет
то соответствующее повышение температуры будет
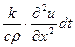 . (24)
. (24)
С другой стороны, это повышение температуры 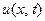 в точке
в точке  за время
за время 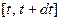 равно
равно
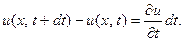 (25)
(25)
Приравнивая друг к другу выражения (23) и (24), и, полагая для краткости, 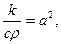 получим уравнение теплопровод- ности
получим уравнение теплопровод- ности
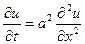 . (26)
. (26)
Таким образом, мы приходим к двум математическим задачам:
А) Найти то решение уравнения (26), которое удовлетво -ряет начальному условию (20) и граничным условиям (21).
В) То же с заменой условий (21) на (23).
Применим к задаче А) метод Фурье. Для этого сначала ре- шим вспомогательную задачу: найти функцию 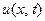 не рав- ную нулю тождественно, удовлетворяющую уравнению (26) и граничным условиям (21) и имеющую специальный вид
не рав- ную нулю тождественно, удовлетворяющую уравнению (26) и граничным условиям (21) и имеющую специальный вид
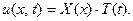 (27)
(27)
Как и при решении уравнения колебания струны, легко по- казать, что из (21) следует
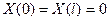 . (28)
. (28)
Подставляя (26) в (27), получим
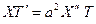 ,
,
т.е.
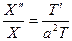 . (29)
. (29)
Соотношение (29) возможно лишь тогда, когда обе его части представляют одну и ту же постоянную. Обозначим её через 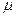 . На основании (28), допущения
. На основании (28), допущения 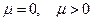 невоз-
невоз-
можны. Следовательно, 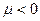 . Полагая
. Полагая 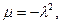 и, букваль -но повторяя рассуждения из 1, по формуле (29) получаем, что
и, букваль -но повторяя рассуждения из 1, по формуле (29) получаем, что
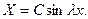
Более того, как и в 1, устанавливаем, что 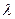 может иметь только одно из значений
может иметь только одно из значений 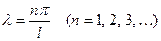 . Следова -тельно,
. Следова -тельно, 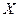 может иметь любое из выражений
может иметь любое из выражений
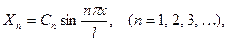
где 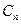 - произвольные постоянные. Выбирая какое – либо из возможных значений
- произвольные постоянные. Выбирая какое – либо из возможных значений 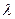 и приравнивая правую часть равенс- тва (29) величине
и приравнивая правую часть равенс- тва (29) величине 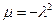 , находим
, находим
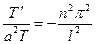 ,
,
т.е.
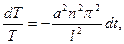
откуда,
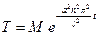 ,
,
где 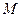 - произвольная постоянная. Полагая
- произвольная постоянная. Полагая 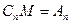 , находим бесконечное множество решений вспомогательной за -дачи
, находим бесконечное множество решений вспомогательной за -дачи
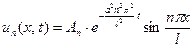 . (30)
. (30)
Каждая из этих функций при любых 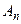 удовлетворяет уравнению (26) и граничным условиям (21). Ввиду линейности уравнения и граничных условий, сумма
удовлетворяет уравнению (26) и граничным условиям (21). Ввиду линейности уравнения и граничных условий, сумма
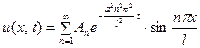 (31)
(31)
при любом выборе 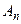 , сохраняющем сходимость написанного ряда, также будет решением (26), удовлетворяющим (21). По- стараемся же подобрать
, сохраняющем сходимость написанного ряда, также будет решением (26), удовлетворяющим (21). По- стараемся же подобрать 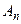 так, чтобы удовлетворить и на -чальному условию
так, чтобы удовлетворить и на -чальному условию 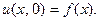 Ясно, что это приводит к равенству
Ясно, что это приводит к равенству
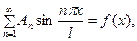
откуда
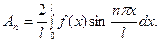 (32)
(32)
Итак задача А) решена. Её решение даётся формулой (31), в которой 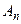 нужно вычислять по (32).
нужно вычислять по (32).
Полезно заметить, что из (31) следует, что
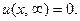
Физический смысл этого соотношения ясен: всё тепло из стержня вытечет и в нём установится температура льда, в который погружены его концы.
Перейдём к задаче В). Для неё вспомогательная задача состоит в нахождении функции 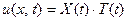 не равной нулю тождественно, удовлетворяющей уравнению (26) и усло- виям (23) Последние дают:
не равной нулю тождественно, удовлетворяющей уравнению (26) и усло- виям (23) Последние дают:
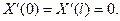 (33)
(33)
Подстановка 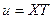 в (26) снова приводит к уравнению
в (26) снова приводит к уравнению
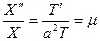 , (34)
, (34)
где 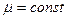 . Случай
. Случай 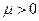 исключается, как и выше. Но соотношение
исключается, как и выше. Но соотношение 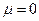 уже возможно. Оно даёт :
уже возможно. Оно даёт : 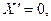 откуда
откуда
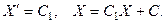 Согласно (33), будет
Согласно (33), будет 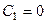 и потому
и потому 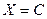 , где
, где 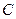 - произвольная постоянная. Кроме того, при
- произвольная постоянная. Кроме того, при 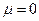 уравнение (34) даёт
уравнение (34) даёт 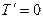 , т.е. и
, т.е. и 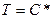 , где
, где 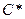 - постоянная. Следовательно, одним из решений вспомога -тельной задачи будет
- постоянная. Следовательно, одним из решений вспомога -тельной задачи будет
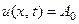 .
.
При любом выборе 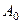 (хотя бы и
(хотя бы и 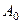 = 0) эта функция удо -влетворяет соотношениям (26) и (23).
= 0) эта функция удо -влетворяет соотношениям (26) и (23).
Предположим теперь, что 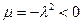 . Это даёт уравнение
. Это даёт уравнение
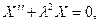
решение которого имеет вид:
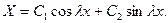
Но тогда
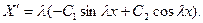
и первое из соотношений (33) даёт 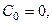 так что (после замены
так что (после замены 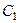 на
на 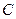 ) принимает вид
) принимает вид
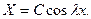
Отсюда и из второго условия (69) получим
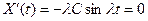 .
.
Значит, 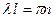
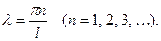 (35)
(35)
Таким образом, найдено бесконечное множество выражений функции 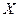 :
:
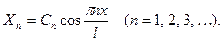
Подставив в (34) одно из значений (35), получим
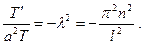
Отсюда
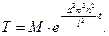
Положив 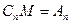 , находим бесконечное множество функций
, находим бесконечное множество функций
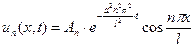 ,
,
удовлетворяющих (26) и (23). Но тогда и
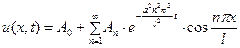 (36)
(36)
будет решением (26), удовлетворяющим (23). Остаётся подо -брать 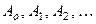 так, чтобы оказалось
так, чтобы оказалось 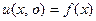 , т.е.
, т.е.
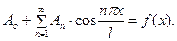
Для этого необходимо взять
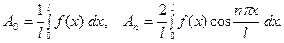 (37)
(37)
Замечание. Из (36) видим, что
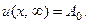
Этим выражен физически очевидный факт, что с течением времени температура в изолированном стержне вырав- нивается. Более того, ясно и значение этой выровненной температуры. Именно, найдём общее количество тепла, содержащегося в нашем стержне. Для этого выделим из него элемент 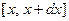 . В начальный момент температура этого элемента равна
. В начальный момент температура этого элемента равна  . Поскольку масса элемента равна
. Поскольку масса элемента равна 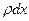 , то для получения указанной температуры нужно было накопить в элементе
, то для получения указанной температуры нужно было накопить в элементе 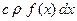 калорий.
калорий.
Стало быть, общее количество тепла в стержне будет равно
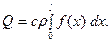
Поскольку стержень изолирован, то это же количество тепла сохранится в нём и при 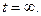 На единицу массы стержня придётся
На единицу массы стержня придётся
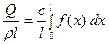
калорий. Это количество тепла и создаёт в стержне температуру
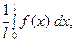
найденную выше.
§ 7 ПРЕОБРАЗОВАНИЕ ФУРЬЕ.
Одним из мощных средств исследования задач математической физики является метод интегральных преобразований.
Пусть функция  задана на интервале
задана на интервале 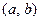 , конечном или бесконечном. Интегральным преобразованием функции
, конечном или бесконечном. Интегральным преобразованием функции  называется функция
называется функция
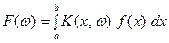 ,
, 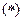
где 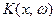 фиксированная для данного преобразования функция, называемая ядром преобразования (предполагается, что интеграл (*) существует в собственном или несобственном смысле).
фиксированная для данного преобразования функция, называемая ядром преобразования (предполагается, что интеграл (*) существует в собственном или несобственном смысле).
Интеграл Фурье
Всякая функция 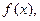 которая на отрезке
которая на отрезке 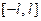 удовлет- воряет условиям разложимости в ряд Фурье, может быть на этом отрезке представлена тригонометрическим рядом
удовлет- воряет условиям разложимости в ряд Фурье, может быть на этом отрезке представлена тригонометрическим рядом
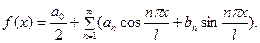 (1) Коэффициенты
(1) Коэффициенты 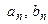 ряда (1) вычисляются по формулам
ряда (1) вычисляются по формулам
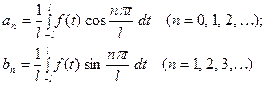 (2)
(2)
Ряд в правой части равенства (1) можно записать в другой форме. С этой целью внесём в него из формул (2) значения коэффициентов 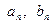 , подведём под знаки интегралов
, подведём под знаки интегралов 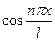 и
и 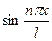 (это возможно, поскольку переменной интегрирования является
(это возможно, поскольку переменной интегрирования является 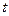 ) и используем формулу для косинуса разности. Будем иметь:
) и используем формулу для косинуса разности. Будем иметь:
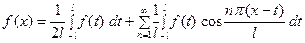 . (3)
. (3)
Если функция  первоначально была на интервале числовой оси, большем, чем
первоначально была на интервале числовой оси, большем, чем 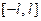 (например на всей оси), то разложение (3) воспроизведёт значение этой функции на отрезке
(например на всей оси), то разложение (3) воспроизведёт значение этой функции на отрезке 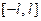 и продолжит её на всю числовую прямую, как периодическую функцию, с пери -одом
и продолжит её на всю числовую прямую, как периодическую функцию, с пери -одом 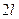 . Поэтому, если функция
. Поэтому, если функция  (вообще говоря, непериодическая) определена на всей числовой оси, в формуле (3) можно перейти к пределу при
(вообще говоря, непериодическая) определена на всей числовой оси, в формуле (3) можно перейти к пределу при 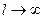 . При этом естественно потребовать выполнения следующих условий:
. При этом естественно потребовать выполнения следующих условий:
1).  удовлетворяет условиям разложимости в ряд Фурье на любом конечном отрезке оси Ох;
удовлетворяет условиям разложимости в ряд Фурье на любом конечном отрезке оси Ох;
2). Функция  абсолютно интегрируема на всей чис -ловой оси,
абсолютно интегрируема на всей чис -ловой оси,
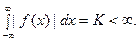 (4)
(4)
При выполнении условия 2) первое слагаемое правой части равенства (3) при 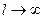 стремится у нулю. В самом деле,
стремится у нулю. В самом деле,
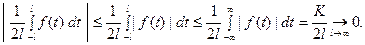
Попытаемся установить, во что перейдёт в пределе при 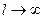 сумма в правой части (3). Положим
сумма в правой части (3). Положим
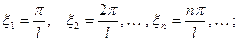
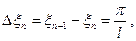
так, что 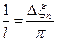 . Тогда сумма в правой части (3) примет вид
. Тогда сумма в правой части (3) примет вид
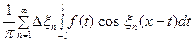 . (5)
. (5)
В силу абсолютной сходимости интеграла, эта сумма, при больших 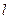 , мало отличается от выражения
, мало отличается от выражения
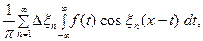
которое напоминает интегральную сумму для функции пере -менного 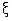
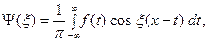
составленную для интервала 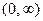 изменения
изменения 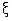 . Поэтому естественно ожидать, что , при
. Поэтому естественно ожидать, что , при 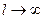 , (
, ( 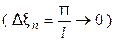 сумма (5) перейдёт в интеграл
сумма (5) перейдёт в интеграл
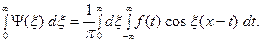
С другой стороны, при 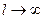 (
(  фиксировано) из фор -мулы (3) вытекает, что
фиксировано) из фор -мулы (3) вытекает, что
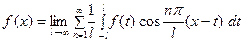 , (6)
, (6)
и мы получаем равенство
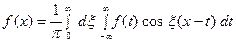 . (7)
. (7)
Достаточное условие справедливости формулы (7) выражается следующей теоремой
ТЕОРЕМА 1. Если функция  абсолютно интегрируема на всей числовой оси
абсолютно интегрируема на всей числовой оси 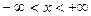 и имеет вместе со своей производной конечное число точек разрыва первого рода на любом отрезке
и имеет вместе со своей производной конечное число точек разрыва первого рода на любом отрезке 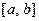 , то справедливо равенство
, то справедливо равенство
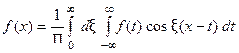
При этом во всякой точке 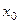 , являющейся точкой разрыва 1-го рода функции
, являющейся точкой разрыва 1-го рода функции  , значение интеграла в правой части (7) равно
, значение интеграла в правой части (7) равно 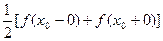
Формулу (7) называют интегральной формулой Фурье, а стоящий в её правой части интеграл - интегралом Фурье. Если воспользоваться формулой для косинуса разности, то формулу (7) можно записать в виде
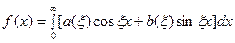 , (8) где
, (8) где
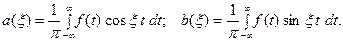 (9)
(9)
Функции 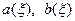 являются аналогами соответствующих ко - эффициентов Фурье
являются аналогами соответствующих ко - эффициентов Фурье 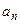 и
и 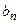
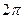 - периодической функции, но последние определены для дискретных значений
- периодической функции, но последние определены для дискретных значений  , в то время как
, в то время как 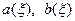 определены для непрерывных значений
определены для непрерывных значений 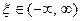 .
.
2. Комплексная форма интеграла Фурье.
Предполагая  абсолютно интегрируемой на всей оси Ох, рассмотрим интеграл
абсолютно интегрируемой на всей оси Ох, рассмотрим интеграл
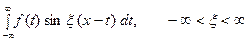 .
.
Этот интеграл равномерно сходится для 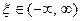 , так как
, так как 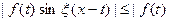 и потому представляет собой не- прерывную и, очевидно, нечётную функцию от
и потому представляет собой не- прерывную и, очевидно, нечётную функцию от 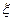 . Но тогда
. Но тогда 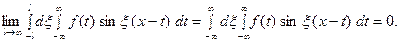 С другой стороны, интеграл
С другой стороны, интеграл
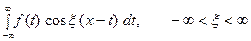
является чётной функцией от переменной 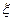 , так что
, так что 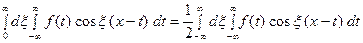 Следовательно, интегральную формулу Фурье можно записать так
Следовательно, интегральную формулу Фурье можно записать так
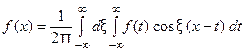 . (10)
. (10)
Умножим равенство
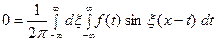
на мнимую единицу 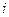 и прибавим к равенству (10). Получим
и прибавим к равенству (10). Получим 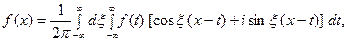 Отсюда, в силу формулы Эйлера (
Отсюда, в силу формулы Эйлера ( 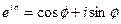 ), будем иметь
), будем иметь 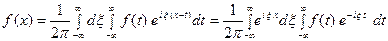
(11) Это комплексная форма интеграла Фурье. Здесь внешнее ин- тегрирование по 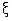 понимается в смысле главного значения по Коши
понимается в смысле главного значения по Коши 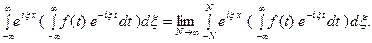
3. Косинус - и синус – преобразования Фурье.
Пусть функция  является кусочно гладкой на любом конечном отрезке оси Ох и абсолютно интегрируема на всей оси.
является кусочно гладкой на любом конечном отрезке оси Ох и абсолютно интегрируема на всей оси.
ОПРЕДЕЛЕНИЕ. 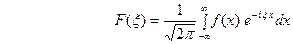 (12) называется преобразование Фурье функции
(12) называется преобразование Фурье функции  (спект- ральной функцией ). интегральноеное преобразование функции
(спект- ральной функцией ). интегральноеное преобразование функции  на интервале
на интервале 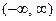 с ядром
с ядром 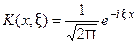 . Используя интегральную формулу Фурье
. Используя интегральную формулу Фурье
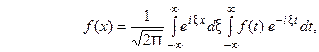 Получаем
Получаем 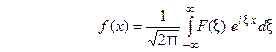 (13) это так называемое обратное преобразование Фурье, дающее переход от
(13) это так называемое обратное преобразование Фурье, дающее переход от 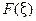 к
к 
Иногда прямое преобразование Фурье задают так
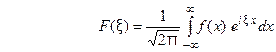 (14) Тогда обратное преобразование Фурье определяется форму -лой
(14) Тогда обратное преобразование Фурье определяется форму -лой 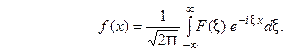 (15)
(15)
Преобразование Фурье 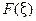 функции
функции  определяют также следующим образом
определяют также следующим образом
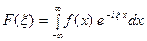 . (16) Тогда, в сою очередь,
. (16) Тогда, в сою очередь,
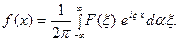 (17)
(17)
При этом положение множителя 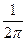 достаточно произ- вольно: он может входить либо в формулу (16) либо в формулу (17).
достаточно произ- вольно: он может входить либо в формулу (16) либо в формулу (17).
ПРИМЕР 1. Найти преобразование Фурье функции
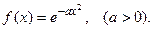
Имеем
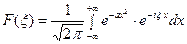 (18)
(18)
Это равенство допускает дифференцирование по 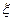 под знаком интеграла (получающийся после дифференцирования интеграл равномерно сходится, когда
под знаком интеграла (получающийся после дифференцирования интеграл равномерно сходится, когда 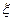 принадлежит любому конечному отрезку)
принадлежит любому конечному отрезку)
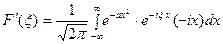 . Интегрируя по частям, будем иметь:
. Интегрируя по частям, будем иметь:
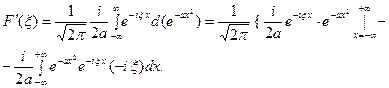 Внеинткгральное слагаемое обращается в нуль и мы получа- ем
Внеинткгральное слагаемое обращается в нуль и мы получа- ем 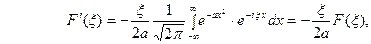 Откуда
Откуда
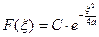 (19) (С - постоянная интегрирования). Полагая в (19)
(19) (С - постоянная интегрирования). Полагая в (19) 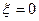 , найдём
, найдём 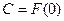 . В силу (18), имеем
. В силу (18), имеем
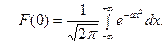
Известно, что 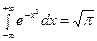 . Поэтому
. Поэтому 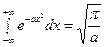 и значит
и значит 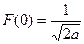 . Таким образом,
. Таким образом, 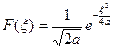 . В частности, для
. В частности, для 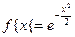 ,
, 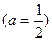 получаем, что
получаем, что 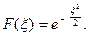
ПРИМЕР 2.. (разряд конденсатора через сопротивление). Рассмотрим 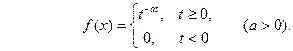
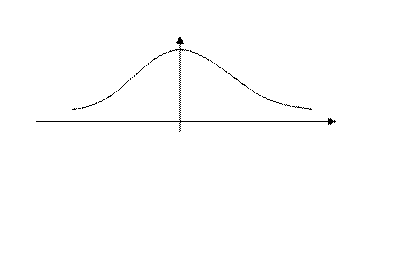 Для спектральной функции
Для спектральной функции 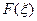 получаем
получаем 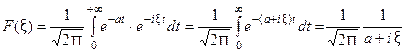 Отсюда
Отсюда 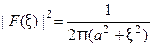 , (см. рис. 14).
, (см. рис. 14).
У
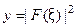
О Х
Рис. 14
Условие абсолютной интегрируемости функции  на всей числовой оси является весьма жёстким. Оно исключает, например, такие элементарные функции, как
на всей числовой оси является весьма жёстким. Оно исключает, например, такие элементарные функции, как 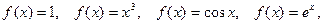 для которых преобразования Фурье (в рассматриваемой здесь классической форме) не существует. Фурье – образ имеют только те функции, которые достаточно быстро стремятся к нулю при
для которых преобразования Фурье (в рассматриваемой здесь классической форме) не существует. Фурье – образ имеют только те функции, которые достаточно быстро стремятся к нулю при 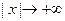 (как в примерах 1. и 2.)..
(как в примерах 1. и 2.)..
Используя формулу косинуса разности, перепишем интег- ральную формулу Фурье
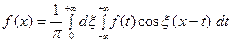 в следующем виде:
в следующем виде:
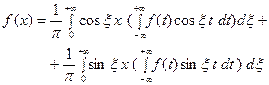 (20
(20
Пусть  - чётная функция. Тогда
- чётная функция. Тогда
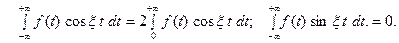
Так что из равенства (20) имеем
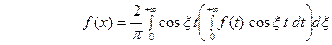 . (21) В случае нечётной функции
. (21) В случае нечётной функции  аналогично получаем
аналогично получаем 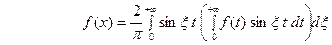 . (22)
. (22)
Если функция  задана лишь на
задана лишь на 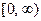 , то формула (21) продолжает
, то формула (21) продолжает  на всю ось Ох чётным образом, а формула (22) - нечётным.
на всю ось Ох чётным образом, а формула (22) - нечётным.
ОПРЕДЕЛЕНИЕ. 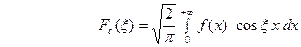 (23) ( называется косинус – преобразованием Фурье функции
(23) ( называется косинус – преобразованием Фурье функции  .
.
Из (21) следует, что для чётной функции 
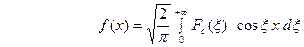 . (24) Это означает, что
. (24) Это означает, что  , в свою очередь, является косинус - преобразованием для
, в свою очередь, является косинус - преобразованием для 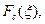 Иными словами, функции
Иными словами, функции  и
и 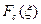 являются взаимными косинус – преобразованиями.
являются взаимными косинус – преобразованиями.
ОПРЕДЕЛЕНИЕ 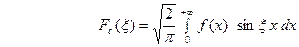 . (25) называется синус – преобразованием функции
. (25) называется синус – преобразованием функции  . Из (22) получаем, что для нечётной функции
. Из (22) получаем, что для нечётной функции 
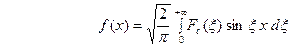 , (26) т.е.
, (26) т.е.  и
и 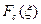 являются взаимными синус – преобразова -ниями.
являются взаимными синус – преобразова -ниями.
4, Свойства преобразования Фурье.
1. Линейность. Если 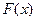 и
и 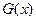 - преобразования Фурье функций
- преобразования Фурье функций  и
и 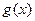 соответственно, то при любых постоянных
соответственно, то при любых постоянных 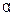 и
и 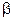 преобразованием Фурье функции
преобразованием Фурье функции 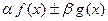 является функция
является функция 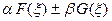 .
.
Пользуясь свойством линейности интеграла, имеем 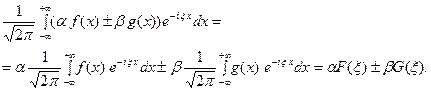 Таким образом, преобразование Фурье - это линейный оператор. Обозначив его через
Таким образом, преобразование Фурье - это линейный оператор. Обозначив его через 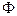 , будем писать
, будем писать 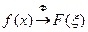 или
или 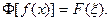
2. Если 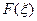 - преобразование Фурье абсолютно интегрируемой на всей числовой прямой функции
- преобразование Фурье абсолютно интегрируемой на всей числовой прямой функции  , то
, то 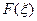 ограничено при всех
ограничено при всех 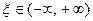 .
.
В самом деле, пусть функция  абсолютно интегрируема на всей оси
абсолютно интегрируема на всей оси 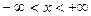 ,
,
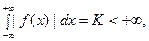
и пусть
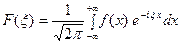 - преобразование Фурье функции
- преобразование Фурье функции  . Тогда
. Тогда
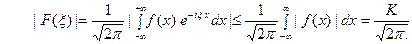 3. Преобразование Фурье и операция дифференцирования. Пусть абсолютно интегрируемая функция
3. Преобразование Фурье и операция дифференцирования. Пусть абсолютно интегрируемая функция  имеет производную
имеет производную 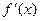 также абсолютно интегрируемую на всей оси Ох, так что
также абсолютно интегрируемую на всей оси Ох, так что  стремится к нулю при
стремится к нулю при 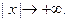 Считая
Считая 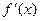 гладкой функцией, запишем
гладкой функцией, запишем 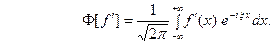 Интегрируя по частям, будем иметь
Интегрируя по частям, будем иметь 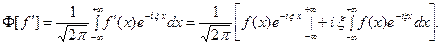 Внеинтегральное слагаемое обращается в ноль, ( так как
Внеинтегральное слагаемое обращается в ноль, ( так как  стремится к нулю при
стремится к нулю при 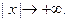 ) и мы получаем
) и мы получаем 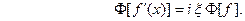 (27) Таким образом, дифференцированию функции
(27) Таким образом, дифференцированию функции  отвечает умножение её образа Фурье
отвечает умножение её образа Фурье 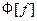 на множитель
на множитель 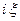 .
.
Если функция  имеет гладкие абсолютно интегрируемые производные до порядка
имеет гладкие абсолютно интегрируемые производные до порядка 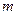 включительно и все они, как и сама функция
включительно и все они, как и сама функция  , стремятся к нулю при
, стремятся к нулю при 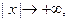 то, интегрируя по частям нужное число раз, получим
то, интегрируя по частям нужное число раз, получим 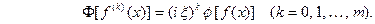 (28)
(28)
Преобразование Фурье очень полезно именно потому, что оно заменяет операцию дифференцирования операцией умножения на величину 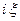 и тем самым упрощает задачу интегрирования некоторых видов дифференциальных уравнений.
и тем самым упрощает задачу интегрирования некоторых видов дифференциальных уравнений.
Так как преобразование Фурье 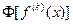 абсолютно интегрируемой функции
абсолютно интегрируемой функции 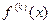 является ограниченной функцией от
является ограниченной функцией от 
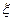 (свойство 2), то из соотношения (28) получаем для
(свойство 2), то из соотношения (28) получаем для 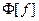 следующую оценку:
следующую оценку:
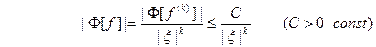 Из этой оценки следует: чем больше функция
Из этой оценки следует: чем больше функция  имеет абсолютно интегрируемых производных, тем быстрее её преобразование Фурье стремится к нулю при
имеет абсолютно интегрируемых производных, тем быстрее её преобразование Фурье стремится к нулю при 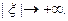 Замечание. Условие
Замечание. Условие 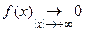 является достаточно естественным, поскольку обычная теория интегралов Фурье имеет дело с процессами, которые в том или ином смысле имеют начало и конец, но не продолжаются неограниченно с примерно одинаковой интенсивностью.
является достаточно естественным, поскольку обычная теория интегралов Фурье имеет дело с процессами, которые в том или ином смысле имеют начало и конец, но не продолжаются неограниченно с примерно одинаковой интенсивностью.
5 Связь между скоростью убывания функции  при
при 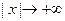 и гладкостью её преобразования Фурье.
и гладкостью её преобразования Фурье.
Предположим, что не только  , но и её произведение
, но и её произведение 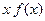 являются абсолютно интегрируемыми функциями на всей оси Ох. Тогда преобразование Фурье
являются абсолютно интегрируемыми функциями на всей оси Ох. Тогда преобразование Фурье
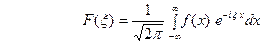 функции
функции  будет дифференцируемой функцией. Действительно, формальное дифференцирование по параметру
будет дифференцируемой функцией. Действительно, формальное дифференцирование по параметру 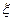 подынтегральной функции приводит к интегралу
подынтегральной функции приводит к интегралу 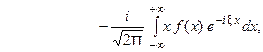 который является абсолютно и равномерно сходящимся относительно параметра
который является абсолютно и равномерно сходящимся относительно параметра 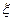 . Следовательно, дифференци -рование возможно, и
. Следовательно, дифференци -рование возможно, и
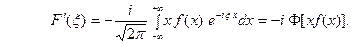 Таким образом,
Таким образом,
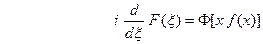 , т.е. операция умножения
, т.е. операция умножения  на аргумент
на аргумент  переходит после преобразования Фурье в операцию
переходит после преобразования Фурье в операцию 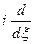 .
.
Если вместе с функцией  абсолютно интегрируемыми на всей числовой прямой Ох являются функции
абсолютно интегрируемыми на всей числовой прямой Ох являются функции 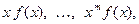 то процесс дифференцирования можно продолжить. Получим, что функция
то процесс дифференцирования можно продолжить. Получим, что функция 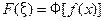 имеет производные до порядка
имеет производные до порядка 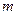 включительно, причём
включительно, причём 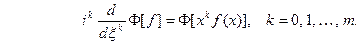 Таким образом, чем быстрее функция
Таким образом, чем быстрее функция  убывает при
убывает при 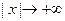 , тем более гладкой получается функция
, тем более гладкой получается функция 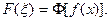
ТЕОРЕМА (о свёртке). Пусть функции 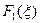 и
и 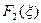 - преобразования Фурье функций
- преобразования Фурье функций 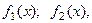 соответственно. Тогда
соответственно. Тогда 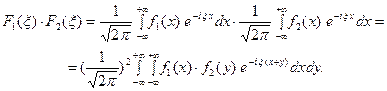
Причём двойной интеграл в правой части сходится абсолютно.
В самом деле, положим 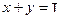 , так что
, так что 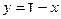 . Тогда будем иметь
. Тогда будем иметь
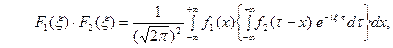 или, меняя порядок интегрирования,
или, меняя порядок интегрирования,
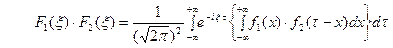 . Функция
. Функция 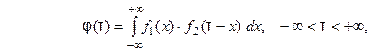 называется свёрткой функций
называется свёрткой функций 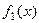 и
и 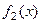 , и обозначается символом
, и обозначается символом 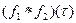 . Поэтому можем записать
. Поэтому можем записать 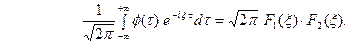 Поэтому видим, что преобразование Фурье свёртки функций
Поэтому видим, что преобразование Фурье свёртки функций 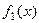 и
и 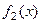 равно умноженному на
равно умноженному на 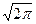 произведению преобразований Фурье свёртываемых функций,
произведению преобразований Фурье свёртываемых функций, 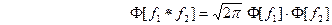
 6. Приложения преобразований Фурье.
6. Приложения преобразований Фурье.
ПРИМЕР 1. Пусть 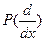 - линейный дифферен- циальный оператор порядка
- линейный дифферен- циальный оператор порядка 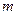 с постоянными коэф- фициентами,
с постоянными коэф- фициентами,
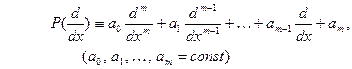
Используя формулу для преобразования Фурье функции
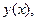 находим
находим
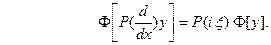 Рассмотрим дифференциальное уравнение
Рассмотрим дифференциальное уравнение
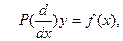 (1) где
(1) где 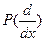 - введённый выше дифференциальный оператор. Предположим, что искомое решение
- введённый выше дифференциальный оператор. Предположим, что искомое решение 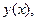 имеет преобразование Фурье
имеет преобразование Фурье 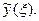 Применяя преобразование Фурье к уравнению (1), получим вместо дифференциального алгебраическое уравнение на оси
Применяя преобразование Фурье к уравнению (1), получим вместо дифференциального алгебраическое уравнение на оси 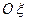 относительно
относительно 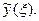 ,
, 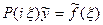 , откуда
, откуда 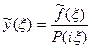 , так что формально
, так что формально 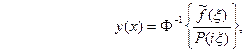 где символ
где символ 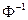 обозначает обратное преобразование Фурье.
обозначает обратное преобразование Фурье.
ПРИМЕР 2 Найти решение 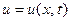 уравнения
уравнения 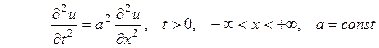 (2) при начальных условиях
(2) при начальных условиях
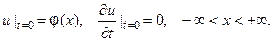 (3) Это - задача о свободных колебаниях бесконечной одно -родной струны, когда задано начальное отклонение
(3) Это - задача о свободных колебаниях бесконечной одно -родной струны, когда задано начальное отклонение 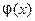 точек струны, а начальные скорости отсутствуют.
точек струны, а начальные скорости отсутствуют.
Поскольку пространственная переменная  изменяется в предедах от
изменяется в предедах от 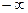 до
до 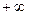 , подвергнем уравнение и на- чальные условия преобразованию Фурье по переменной
, подвергнем уравнение и на- чальные условия преобразованию Фурье по переменной  . Будем предполагать, что
. Будем предполагать, что
1) функции 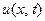 и
и 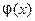 - достаточно гладкие и стремятся к нулю при
- достаточно гладкие и стремятся к нулю при 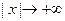
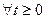 настолько быстро, что существуют преобразования Фурье
настолько быстро, что существуют преобразования Фурье
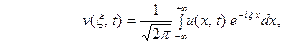 (4)
(4) 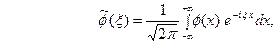 (5)
(5)
2) допустимы операции дифференцирования, так что 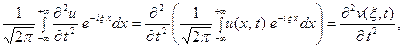
(6) 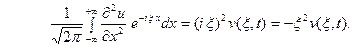 (7) Умножая обе части (2) на
(7) Умножая обе части (2) на 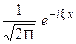 и интегрируя по
и интегрируя по  от
от 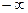 до
до 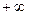 , получим:
, получим:
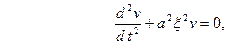 (8) а из начальных условий (3) найдём
(8) а из начальных условий (3) найдём
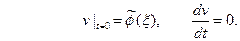 (9) Таким образом, применяя к задаче (2) – (3) преобразование Фурье, приходим к задаче Коши (8) – (9) для обыкновенного дифференциального уравнения, где
(9) Таким образом, применяя к задаче (2) – (3) преобразование Фурье, приходим к задаче Коши (8) – (9) для обыкновенного дифференциального уравнения, где 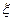 - параметр. Решением уравнения (8) является функция
- параметр. Решением уравнения (8) является функция
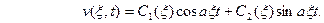 Из условий (9) находим, что
Из условий (9) находим, что 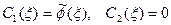 , и
, и
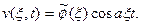 Применяя обратное преобразование Фурье, получим
Применяя обратное преобразование Фурье, получим 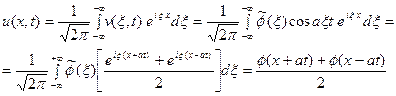 Это частный случай формулы Даламбера решения задачи.
Это частный случай формулы Даламбера решения задачи.
ПРИМЕР 3. Преобразование Фурье может быть использовано при решении некоторых интегральных уравнений, т.е. уравнений, в которых неизвестная функция входит под знак интеграла. Рассмотрим, например, уравнение
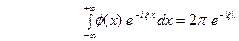 (10) где
(10) где 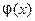 - искомая функция. Записав (10) в виде
- искомая функция. Записав (10) в виде 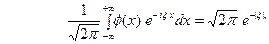 (11) замечаем, что левую часть (11) можно рассматривать как преобразование Фурье функции
(11) замечаем, что левую часть (11) можно рассматривать как преобразование Фурье функции 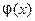 , так что (11) равносильно следующему равенству
, так что (11) равносильно следующему равенству
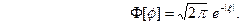 Тогда по формуле обращения
Тогда по формуле обращения
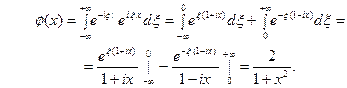 Функция
Функция 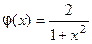 является решением уравнения (10).
является решением уравнения (10).
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Воробьёв Н.Н. Теория рядов. - М.: Наука, 1975.
2. Винер Н. Интеграл Фурье и некоторые его приложения. - М. Физматгиз, 1983.
3. Ефимов А.В. Математический анализ (специальные разделы), ч. 1. – М.: Высш. шк., 1980.
4. Краснов М.Л., Киселёв А.И., Макаренко Г.И., Шикин Е.В., Заляпин В.И., Соболев С.К. Вся высшая математика, т.4, - М.Эдиториал, 2001.
5. Натансон И.П. Краткий курс высшей математики. – Санкт - Петербург, 2001.
6. Харди Г.Х., Рогозинский В.В. Ряды Фурье - М. Физматгиз, 1959.
СОДЕРЖАНИЕ
1. ЭЛЕМЕНТЫ ТЕОРИИ ЧИСЛОВЫХ РЯДОВ
§ 1. Понятие числового ряда ………………………………… 3
§ 2. Числовые ряды с положительными членами
Необходимые и достаточные признаки сходимости … 8
§ 3. Знакопеременные ряды ……………………………………. 19
2. ЭЛЕМЕНТЫ ФУНКЦИОНАЛЬНЫХ РЯДОВ.
§ 1. Определение функционального ряда. …………………. 23
§ 2. Степенные ряды ……………………………………………. 28
§ 3. Ряд Тейлора. Применение степенных рядов
в приближённых вычислениях …………………………. 35
2. РЯДЫ ФУРЬЕ.
§ 1. Вводные замечания. ……………………………………… 42
§ 2. Теорема единственности. Ряд Фурье. ……………….. . 45
§ 3. Ряд Фурье для чётных и нечётных функций.
Разложение функции, заданной на части
промежутка. Сдвиг основного промежутка …………… 56
§ 4. Ряд Фурье для функции с произвольным
периодом ……………………………………………………. 65
§ 5. Ряд Фурье в комплексной форме …………………….. 70
§ 6. Приложения рядов Фурье. ……………………………… 73
§ 7. Преобразование Фурье. …………………………………… 90
БИБЛИОГРАФИЧЕСКИЙ СПИСОК …………………………….110
Дата добавления: 2021-03-18; просмотров: 45; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
