Обычное приближённое вычисление.
1 Вычислить приближённо с точностью до 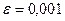
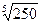 . Преобразуем подкоренное выражение:
. Преобразуем подкоренное выражение: 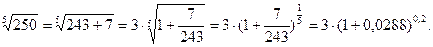 Используя разложение функции 5 в степенной ряд для
Используя разложение функции 5 в степенной ряд для 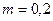 при
при 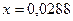 получаем:
получаем:
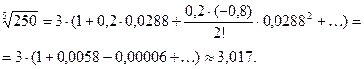
(Мы учли свойство знакопеменных рядов, которое заклю - чается в том, что точность вычисления суммы ряда опреде -ляется величиной первого отбрасываемого слагаемого).
Приближённое вычисление интегралов.
2. Вычислить с точностью 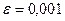 интеграл:
интеграл:
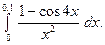
Разложим подынтегральную функцию в степенной ряд:
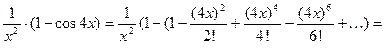

Проинтегрируем полученную функцию:
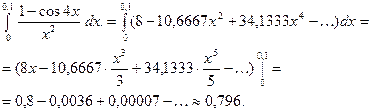
3. Вычислить с точностью 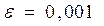 интеграл:
интеграл:
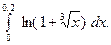
Разложим в степенной ряд подынтегральную функцию 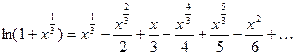 . Тогда
. Тогда
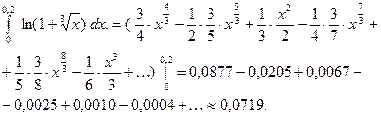
Приближённое решение дифференциальных уравнений.
4. Найти решение дифференциального уравнения в виде разложения его в степенной ряд:
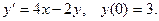
При данном начальном условии, 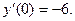 Продифференци - руем данное уравнение:
Продифференци - руем данное уравнение: 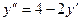 , тогда
, тогда 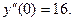 Про –должаем дифференцирование:
Про –должаем дифференцирование:
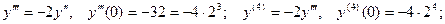
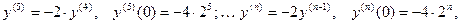 Используя формулу (3), получим решение данного диффе -ренциального уравнения в виде:
Используя формулу (3), получим решение данного диффе -ренциального уравнения в виде:
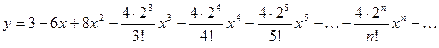 5. Найти пять первых ненулевых члена разложения в сте -пенной ряд решения дифференциального уравнения:
5. Найти пять первых ненулевых члена разложения в сте -пенной ряд решения дифференциального уравнения:
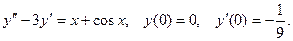
Или 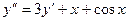 . При данных начальных условиях
. При данных начальных условиях 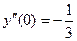 . Продифференцируем уравнение:
. Продифференцируем уравнение:
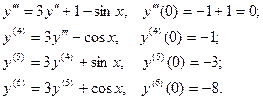
Тогда, по формуле (3), получаем решение дифференнци- ального уравнения в виде ряда:
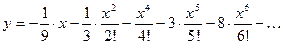 .
.
6. Найти решение дифференциального уравнения:
|
|
|
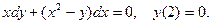
Разделив данное уравнение на 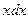 , получим уравнение в виде:
, получим уравнение в виде: 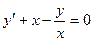 , или
, или 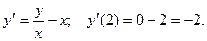
Найдём следующие производные:
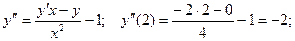
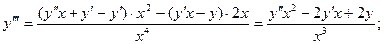
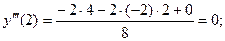
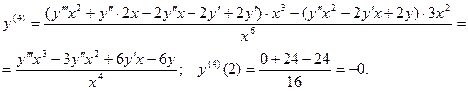
Можно проверить, что если будем вычислять очередные про –изводные в точке 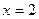 , опять получим нулевые значения.
, опять получим нулевые значения.
Получаем решение дифференциального уравнения в виде: 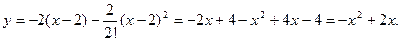
Это точное решение данной задачи Коши дифференци- ального уравнения, что легко проверить непосредственной подстановкой.
6. Найти шесть первых ненулевых члена разложения в
ряд Тейлора решения задачи Коши дифференциального урав -нения:
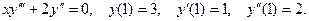
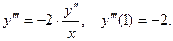
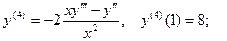
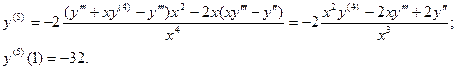 Тогда решение получаем в виде:
Тогда решение получаем в виде:
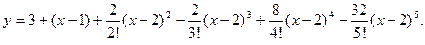
 3. РЯДЫ ФУРЬЕ
3. РЯДЫ ФУРЬЕ
§ 1. ВВОДНЫЕ ЗАМЕЧАНИЯ
Мы знаем, какую большую пользу приносит представление функции в форме:
 (1)
(1)
т.е. в форме суммы степенного ряда. Такое представление даёт возможность и находить приближённо численные значе- ния функции, и устанавливать различные свойства функций, вычислять определённые интегралы, решать дифференци- альные уравнения и т.п. Столь плодотворным представление (1) оказывается потому, что отдельные слагаемые правой части являются чрезвычайно простыми функциями. Можно сказать, что формула (1) показывает, как составлена сложная функция  из простейших функций
из простейших функций
|
|
|
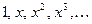 (2)
(2)
Таким образом, разложение (1) в некотором роде сходно с разложением многочлена на множители или с разложением рациональной дроби на простые и т.п.
Наряду с системой степеней (2), в элементарной мате- матике хорошо изучена система тригонометрических функций:
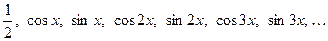 (3)
(3)
Поэтому, кроме представления функции  в форме (1), большое значение имеет её представление в форме суммы ряда по функциям (3), т.е. в форме
в форме (1), большое значение имеет её представление в форме суммы ряда по функциям (3), т.е. в форме
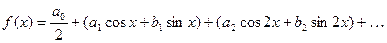 (4)
(4)
Ряд такого вида называется тригонометрическим рядом.
Напомним важное свойство тригонометрических функций:

Если функция 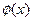 обладает тем свойством, что при неко- торой постоянной
обладает тем свойством, что при неко- торой постоянной 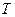 и всех
и всех  оказывается
оказывается
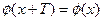 ,
,
то говорят, что функция 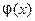 имеет период
имеет период 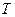 или, короче
или, короче 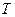 - периодична. Таким образом, все функции системы (3) яв- ляются
- периодична. Таким образом, все функции системы (3) яв- ляются 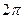 - периодичными. Но тогда и сумма ряда (4) долж- на быть
- периодичными. Но тогда и сумма ряда (4) долж- на быть 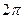 - периодичной: если все члены ряда не меняются от замены
- периодичной: если все члены ряда не меняются от замены  на
на 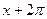 , то и сумма ряда не меняется от такой замены. Поэтому тригонометрические ряды являются аппаратом, особенно удобным для представления
, то и сумма ряда не меняется от такой замены. Поэтому тригонометрические ряды являются аппаратом, особенно удобным для представления 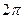 - пери -одических функций.
- пери -одических функций.
|
|
|
Ортогональность тригонометрической системы.
ОПРЕДЕЛЕНИЕ. Две функции  и
и 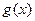 называются взаимно ортогональными на промежутке
называются взаимно ортогональными на промежутке 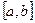 , если
, если
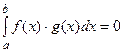 .
.
ТЕОРЕМА 1. Любые две функции системы
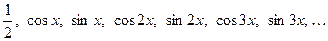 (3)
(3)
взаимно ортогональны на отрезке 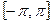 .
.
Доказательство теоремы основано на следующей лемме.
Лемма. Если 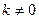 - целое (положительное или отрица- тельное число), то
- целое (положительное или отрица- тельное число), то
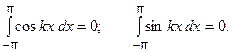 (5)
(5)
В самом деле,
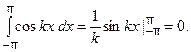
Аналогично доказывается и второе из равенств (5).
Переходя к доказательству теоремы, мы должны выбирать из системы (3) различные пары функций и находить интеграл от их произведения. При этом могут представиться следую- щие случаи.
1) Одна из выбранных функций 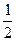 , а вторая -
, а вторая - 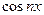 или
или 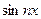 . Тогда упомянутый интеграл будет равен нулю, в силу леммы.
. Тогда упомянутый интеграл будет равен нулю, в силу леммы.
2) Выбрана пара функций 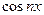 и
и 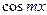 . Так как
. Так как
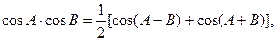 (6)
(6)
тогда
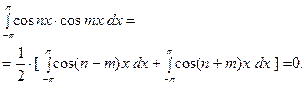
По лемме, оба интеграла, стоящие справа, равны нулю.
3). Выбраны функции 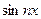 и
и 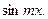 Тогда вместо (6) нужно применить формулу:
Тогда вместо (6) нужно применить формулу:
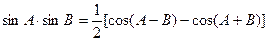
и рассуждать, как в 2).
4) Выбраны функции 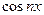 и
и 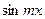 . Так как
. Так как
|
|
|
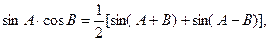
то
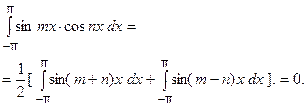
По лемме, оба интеграла справа равны нулю.
Итак, какие бы различные функции из системы (3) ни взять, интеграл от их произведения по промежутку  равен нулю. Это и требовалось доказать.
равен нулю. Это и требовалось доказать.
Нам понадобится ещё
ТЕОРЕМА 2. При любом натуральном  будет
будет
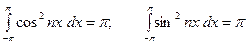 . (7)
. (7)
В самом деле,
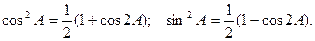 .
.
Отсюда
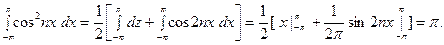
Аналогично доказывается и второе равенство из (7).
§ 2. ТЕОРЕМА ЕДИНСТВЕННОСТИ. РЯД ФУРЬЕ.
ТЕОРЕМА 1. Если функция  , заданная и непрерывная на отрезке
, заданная и непрерывная на отрезке  , разлагается в тригонометрический ряд,
, разлагается в тригонометрический ряд,
то коэффициенты его определяются единственным образом.
Доказательство. Пусть
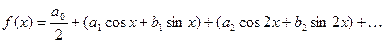 (4)
(4)
Проинтегрируем это равенство по промежутку  , причём в правой части (4) применим формулу: «интеграл суммы равен сумме интегралов». Так как справа стоит бесконечное множество слагаемых, то следовало бы обосновать воз - можность применения указанной теоремы, но мы оставим это в стороне.
, причём в правой части (4) применим формулу: «интеграл суммы равен сумме интегралов». Так как справа стоит бесконечное множество слагаемых, то следовало бы обосновать воз - можность применения указанной теоремы, но мы оставим это в стороне.
Благодаря равенству (5), интегралы от всех слагаемых, кроме первого, равны нулю, что приводит к соотношению
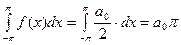 .
.
Отсюда
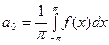 . (8)
. (8)
Итак, свободный член 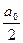 разложения (4) действительно определяется единственным образом.
разложения (4) действительно определяется единственным образом.
Займёмся теперь коэффициентами 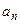 . Запишем формулу (4) в виде:
. Запишем формулу (4) в виде:
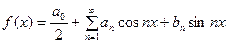 . (4.1)
. (4.1)
Умножим равенство (4.1) на 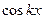 и проинтегрируем полу- ченное равенство по промежутку
и проинтегрируем полу- ченное равенство по промежутку  . Получим
. Получим

Первый интеграл, стоящий справа, равен нулю, по формуле (5). Третий интеграл, стоящий справа, равен нулю. Из вторых интегралов в правой части, равны нулю все интегралы, в ко-
торых 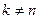 . При
. При 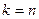 , в силу теоремы 1 и формулы (7), получим
, в силу теоремы 1 и формулы (7), получим
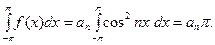
Следовательно,
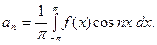 (9)
(9)
Аналогично, если мы умножим ряд (4.1) на 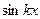 и проин- тегрируем полученное равенство по отрезку
и проин- тегрируем полученное равенство по отрезку  , учитывая аналогичные формулы, получим
, учитывая аналогичные формулы, получим
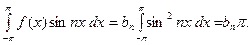
Тогда
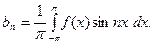 (10)
(10)
Формулы (9) и (10) дают единственные представления для ко- эффициентов 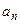 и
и 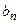 тригонометрического ряда. Теорема до- казана.
тригонометрического ряда. Теорема до- казана.
Эта теорема даёт повод ввести следующее определение.
ОПРЕДЕЛЕНИЕ. Пусть  - функция, заданная на про -межутке
- функция, заданная на про -межутке  . Числа
. Числа 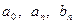 найденные для этой фун-кции по формулам (8), (9), (10) называются её коэффици- ентами Фурье, а ряд
найденные для этой фун-кции по формулам (8), (9), (10) называются её коэффици- ентами Фурье, а ряд
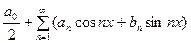
с этими коэффициентами называется рядом Фурье функции  .
.
Из доказательства теоремы 2 видно, что эту теорему можно сформулировать и так:
ТЕОРЕМА 2 (единственности). Если непрерывная на отрез- ке  функция
функция  разлагается в тригонометрический ряд, то это обязательно её ряд Фурье.
разлагается в тригонометрический ряд, то это обязательно её ряд Фурье.
Разумеется, эта теорема вовсе не значит, что всякая непрерывная на отрезке  функция действительно раз- лагается в ряд Фурье. Например, функция
функция действительно раз- лагается в ряд Фурье. Например, функция 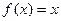 , рассматриваемая на отрезке
, рассматриваемая на отрезке  заведомо не раскла- дывается на всём этом отрезке в тригонометрический ряд, так как у неё
заведомо не раскла- дывается на всём этом отрезке в тригонометрический ряд, так как у неё 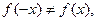 а сумма тригонометрического ряда, ввиду своей
а сумма тригонометрического ряда, ввиду своей 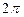 - периодичности в точках
- периодичности в точках 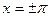 должна иметь одинаковые значения
должна иметь одинаковые значения
ТЕОРЕМА 3 (разложения). Пусть  задана на отрезке
задана на отрезке  и в каждой точке этого промежутка имеет конечную производную
и в каждой точке этого промежутка имеет конечную производную 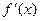 . Тогда ряд Фурье этой функции сходится на всей числовой оси, причём сумма его
. Тогда ряд Фурье этой функции сходится на всей числовой оси, причём сумма его 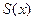 равна
равна  в точках
в точках  , для которых
, для которых 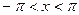 и
и
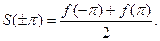 (11)
(11)
Эту замечательную теорему мы примем без доказательства.
Замечание 1. В теореме говорится о том, какова сумма ряда 
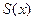 в точках, принадлежащих отрезку
в точках, принадлежащих отрезку  .
.
Однако, поскольку эта сумма 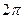 - периодична, то её значения на отрезке
- периодична, то её значения на отрезке  полностью определяют все значения на числовой прямой.
полностью определяют все значения на числовой прямой.
Замечание 2. Теорема гарантирует разложимость всякой дифференцируемой на  функции в ряд Фурье не на всём отрезке, а лишь в открытом промежутке
функции в ряд Фурье не на всём отрезке, а лишь в открытом промежутке 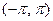 . Одна- ко, если разлагаемая функция удовлетворяет ещё дополни- тельному условию
. Одна- ко, если разлагаемая функция удовлетворяет ещё дополни- тельному условию
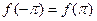 , (12)
, (12)
то, как видно из (11), она будет представлена своим рядом Фурье на всём отрезке  .
.
Введём понятие периодического продолжения функции  , заданной на отрезке
, заданной на отрезке  .
.
ОПРЕДЕЛЕНИЕ. Функция 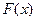 , определённая на всей чи- словой оси и периодическая с периодом
, определённая на всей чи- словой оси и периодическая с периодом 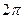 называется периодическим продолжением функции
называется периодическим продолжением функции  , если на отрезке
, если на отрезке  выполняется равенство
выполняется равенство 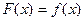 .
.
ОПРЕДЕЛЕНИЕ. Говорят, что функциональный ряд сходится «в среднем» к функции 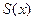 на некотором отрезке
на некотором отрезке 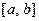 , если последовательность частичных сумм
, если последовательность частичных сумм 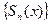 этого ряда сходится «в среднем» к функции
этого ряда сходится «в среднем» к функции 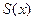 , т.е.
, т.е.
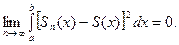
Замечание 3. Очевидно, что, если на отрезке  ряд Фурье сходится к функции
ряд Фурье сходится к функции  , то на всей числовой прямой он сходится к её периодическому продолжению
, то на всей числовой прямой он сходится к её периодическому продолжению 
ТЕОРЕМА 4. Пусть функция  и её производная
и её производная 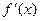 непрерывны на отрезке
непрерывны на отрезке  , или же имеют на этом отрезке конечное число точек разрыва 1 – го рода. Тогда ряд Фурье данной функции сходится на всей числовой прямой, причём в каждой точке
, или же имеют на этом отрезке конечное число точек разрыва 1 – го рода. Тогда ряд Фурье данной функции сходится на всей числовой прямой, причём в каждой точке 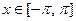 , в которой функция
, в которой функция 
непрерывна, 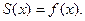 В каждой точке разрыва функции
В каждой точке разрыва функции  сумма ряда равна:
сумма ряда равна:
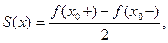 где
где 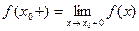 ,
, 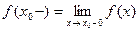 . На концах отрезка
. На концах отрезка  сумма равна
сумма равна
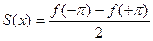 .
.
В любой точке непрерывности  функции
функции 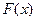 сумма ряда
сумма ряда 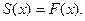 В точках разрыва данной функции сумма ряда равна
В точках разрыва данной функции сумма ряда равна
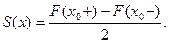
(Здесь, 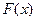 - периодическое продолжение функции
- периодическое продолжение функции  ).
).
ТЕОРЕМА 5. Ряд Фурье кусочно - непрерывной функции  сходится «в среднем» к данной функции на отрезке
сходится «в среднем» к данной функции на отрезке  и к её периодическому продолжению
и к её периодическому продолжению  на всей числовой прямой.
на всей числовой прямой.
ТЕОРЕМА 6. Для любой кусочно - непрерывной функции  , заданной на отрезке
, заданной на отрезке  , для кэффициентов Фурье имеет место равенство Парсеваля:
, для кэффициентов Фурье имеет место равенство Парсеваля:
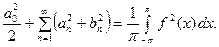
Доказывать эти теоремы не будем.
ПРИМЕРЫ.
При вычислении коэффициентов Фурье необходимо помнить следующие значения:
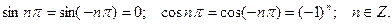
1. Пусть 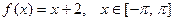 . Найдём коэффициенты Фурье этой функции. По (8),
. Найдём коэффициенты Фурье этой функции. По (8),
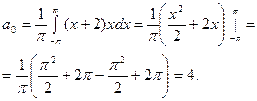 .
.
Далее, интегрируя по частям и применяя (5), находим

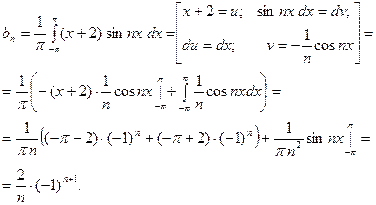
Тогда, по формуле (4.1), получаем
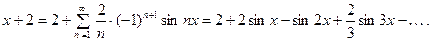
Следует заметить, что последнее равенство верно лишь при 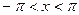 . В случае, если
. В случае, если 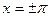 , оно заведомо неверно. Так как
, оно заведомо неверно. Так как  . В силу
. В силу 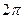 - периодичности суммы
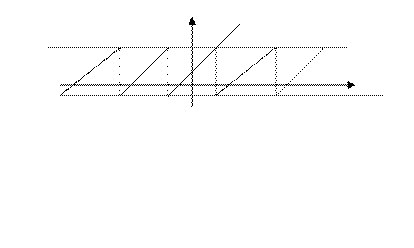
- периодичности суммы 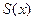 ряда (14), график этой суммы имеет вид, изображённый на рис. 1.
ряда (14), график этой суммы имеет вид, изображённый на рис. 1.
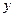
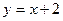
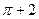
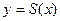
-2 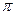 -
- 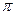 0
0 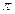 2
2 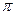

- 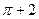 .
.
Рис.1
Интересно, что 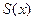 оказывается разрывной функцией (хотя все члены ряда непрерывны). Мы видим, что появление в математике разрывных функций совершенно неизбежно: их вводит сам математический аппарат даже при рассмотрении столь «хороших» функций, как
оказывается разрывной функцией (хотя все члены ряда непрерывны). Мы видим, что появление в математике разрывных функций совершенно неизбежно: их вводит сам математический аппарат даже при рассмотрении столь «хороших» функций, как 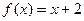 . Систематическим исследованием разрывных функций занимается «Теория функ- ций вещественной переменной».
. Систематическим исследованием разрывных функций занимается «Теория функ- ций вещественной переменной».
2. Пусть 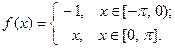 Найдём коэффициенты Фурье этой функции.
Найдём коэффициенты Фурье этой функции.
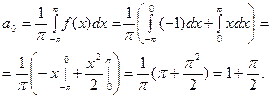
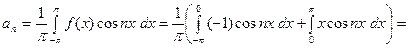
Для второго интеграла
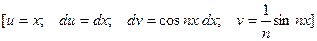
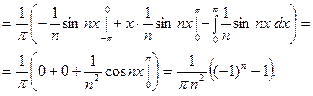
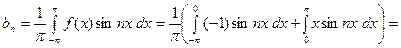
Для второго интеграла
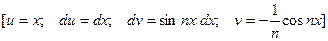
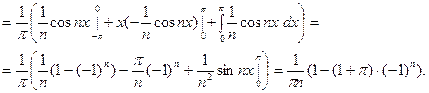
Получаем ряд:
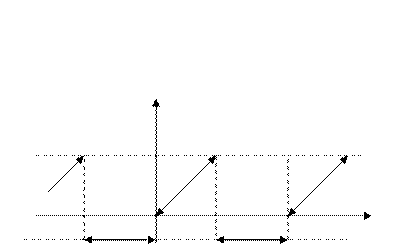
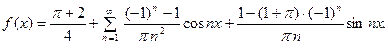
График суммы имеет вид:
 0
0 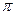
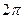

-1
Рис. 2
3. Рассмотрим функцию 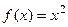 . Её коэффициенты Фурье таковы:
. Её коэффициенты Фурье таковы:
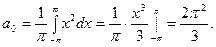
Далее, интегрируя по частям, находим
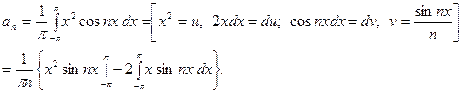
Первое слагаемое равно нулю, так как 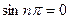 ,,
,,
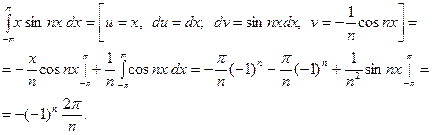 Следовательно,
Следовательно,
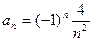 .
.
Аналогичный подсчёт даёт: 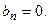 Значит,
Значит,

Так как функция 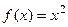 удовлетворяет условию (12), то данное равенство выполнено на всём отрезке
удовлетворяет условию (12), то данное равенство выполнено на всём отрезке  .
.
В частности, полагая 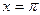 , получим
, получим
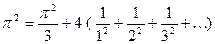 ,
,
откуда вытекает изящное равенство
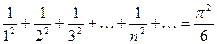 . (13)
. (13)
Замечание. Если (13) умножить на 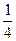 , то получится
, то получится
 .
.
Вычитая это равенство из (13), получим
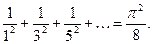 (14)
(14)
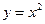
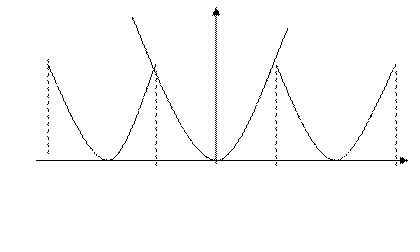


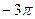

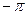 0
0 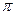
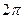
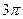
Рис.3
Вследствие 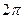 - периодичности суммы
- периодичности суммы 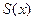 ряда (13) её график имеет вид, изображённый на рис. 3. Функция
ряда (13) её график имеет вид, изображённый на рис. 3. Функция 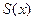 оказывается непрерывной, но не гладкой.
оказывается непрерывной, но не гладкой.
4. Очень поучительно следующее упражнение: пусть функ- ция 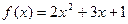 разложена в ряд Фурье и пусть
разложена в ряд Фурье и пусть 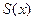 - сумма этого ряда. Найти
- сумма этого ряда. Найти
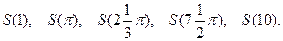
Решение. Точка 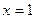 лежит внутри промежутка
лежит внутри промежутка 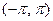 , где
, где 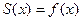 . Значит
. Значит 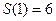 . Далее
. Далее 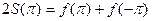 и поэтому
и поэтому 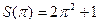 . В силу
. В силу 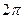 - периодичности
- периодичности 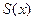 имеем
имеем
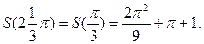
Аналогично,
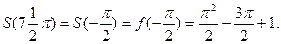
Наконец,
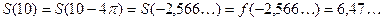 .
.
§ 3. РЯД ФУРЬЕ ДЛЯ ЧЁТНЫХ И НЕЧЁТНЫХ ФУНКЦИЙ.
РАЗЛОЖЕНИЕ ФУНКЦИЙ, ЗАДАННЫХ НА ЧАСТИ
ПРОМЕЖУТКА. СДВИГ ОСНОВНОГО ПРОМЕЖУТКА.
ОПРЕДЕЛЕНИЕ. Функция  называется чётной, если она не меняется при изменении знака её аргумента, т.е. если
называется чётной, если она не меняется при изменении знака её аргумента, т.е. если
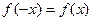 . (1)
. (1)
Примерами чётных функций служат функции 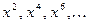 и вообще,
и вообще, 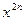 , а также
, а также 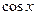 и вообще
и вообще 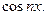 Функция
Функция 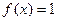 также является чётной.
также является чётной.
Ясно, что график чётной функции симметричен относи-тельно оси ординат.
ОПРЕДЕЛЕНИЕ. Функция  называется нечётной, если при изменении знака аргумента она меняет знак, но сохраняет абсолютную величину, т.е., если
называется нечётной, если при изменении знака аргумента она меняет знак, но сохраняет абсолютную величину, т.е., если
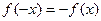 . (2)
. (2)
Например, таковы функции  и вообще
и вообще 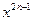 , а также
, а также 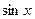 , и вообще,
, и вообще, 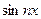 .
.
График нечётной функции симметричен относительно начала координат.
Функция может быть ни чётной, ни нечётной . Например та- кова 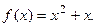 Здесь, например,
Здесь, например, 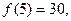 а
а 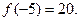
Функция 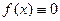 является одновременно и чётной и нечётной.
является одновременно и чётной и нечётной.
Рассмотрим произведение: 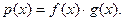 Если
Если  и
и 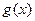 обе чётные или обе нечётные, то
обе чётные или обе нечётные, то 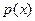 , очевидно, будет чётной. Если же из функций
, очевидно, будет чётной. Если же из функций  и
и 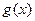 одна чётная, а вторая нечётная, то
одна чётная, а вторая нечётная, то 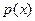 будет нечётной функцией. Иначе говоря, верна следующая
будет нечётной функцией. Иначе говоря, верна следующая
Пусть функция, заданная на отрезке 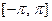 , является чётной, т.е.
, является чётной, т.е. 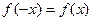 . Тогда её коэффициенты Фурье
. Тогда её коэффициенты Фурье 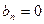 . В самом деле,
. В самом деле,
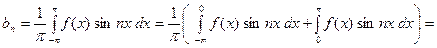 В первом интеграле сделаем замену переменной:
В первом интеграле сделаем замену переменной:
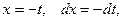 если
если 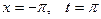 , если
, если 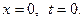
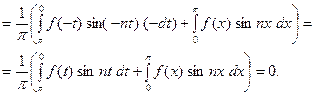
(Если поменять пределы интегрирования в определённом ин -теграле, знак его меняется на противоположный.)
Аналогично, учитывая, что функции  и
и 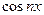 чётные, можно получить следующие формулы:
чётные, можно получить следующие формулы:
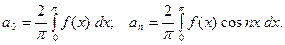
Используя тот же метод, можно доказать, что если функция  нечётная, т.е.
нечётная, т.е. 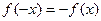 , то её коэффициенты Фурье
, то её коэффициенты Фурье 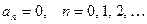 , а коэффициенты Фурье
, а коэффициенты Фурье 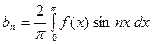 Таким образом, если функция
Таким образом, если функция  чётная, то её ряд Фурье имеет вид:
чётная, то её ряд Фурье имеет вид: 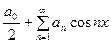 а если нечётная - то
а если нечётная - то 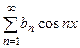 Поэтому с учётом свойства чётности или нечётности функции облегчается разложение функции в ряд Фурье.
Поэтому с учётом свойства чётности или нечётности функции облегчается разложение функции в ряд Фурье.
Дата добавления: 2021-03-18; просмотров: 53; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
