Основных элементарных функций.
Изосова Л.А., Изосов А.В., Грачёва Л.А.
Элементы теории рядов. Учебн. пособие. –
Магнитогорск: МГТУ, 2009. – 111 с.
Рассмотрены основные признаки сходимости числовых поло- жительных и знакопеременных рядов .В разделе функцио- нальных рядов изложены условия сходимости и равномерной сходимости. Продемонстрированы основные прмложения сте -пенных рядов. В разделе: ряды Фурье представлены критерии разложимости функции в тригонометричкские ряды и приложения рядов Фурье. Приведено большое количество примеров, иллюстрирующих излагаемый материал, способству- ющих более глубокому его усвоению.
ЭЛЕМЕНТЫ ТЕОРИИ ЧИСЛОВЫХ РЯДОВ.
§ 1 ПОНЯТИЕ ЧИСЛОВОГО РЯДА.
Пусть задана некоторая числовая последовательность  . Формальная сумма элементов этой последователь –ности:
. Формальная сумма элементов этой последователь –ности:
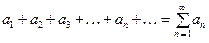 (1) называется числовым рядом. Число
(1) называется числовым рядом. Число 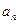 называется общим элементом (общим членом) ряда,
называется общим элементом (общим членом) ряда,  - его порядковым но- мером.
- его порядковым но- мером.
Для каждого натурального числа 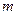 элементов заданной последовательности можно составить конечную сумму
элементов заданной последовательности можно составить конечную сумму
 , (2)
, (2)
которая называется частичной суммой раяда (1). Частичные суммы  сами образуют числовую последовательность, которую можно исследовать на сходимость.
сами образуют числовую последовательность, которую можно исследовать на сходимость.
ОПРЕДЕЛЕНИЕ. Если существует конечный предел частич- ных сумм (2), то он называется суммой ряда (1), т.е.
|
|
|
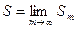 (3) и при этом ряд (1) называется сходящимся. Если предел (3) не существует или бесконечнвй, то ряд (1) называется рас -ходящимся.
(3) и при этом ряд (1) называется сходящимся. Если предел (3) не существует или бесконечнвй, то ряд (1) называется рас -ходящимся.
Рассмотрим несколько примеров применения определения сходимости ряда при исследовании рядов на сходимость.
1. 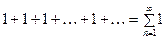 . Для данного ряда
. Для данного ряда  и
и
 . Следовательно, по определению, данный ряд расходится.
. Следовательно, по определению, данный ряд расходится.
2.  . Для данного ряда частичные суммы с чётными номерами
. Для данного ряда частичные суммы с чётными номерами  , а частичные суммы с нечётными номерами
, а частичные суммы с нечётными номерами  . Так как сходящаяся последовательность не может иметь двух раз -личных пределов, то в данном случае последовательность частичных сумм не имеет предела и, следовательно, ряд расходится.
. Так как сходящаяся последовательность не может иметь двух раз -личных пределов, то в данном случае последовательность частичных сумм не имеет предела и, следовательно, ряд расходится.
3. 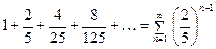 . Этот ряд представляет собой сумму геометрической прогрессии, для которой
. Этот ряд представляет собой сумму геометрической прогрессии, для которой 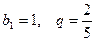 . Сумма геометрической прогрессии вычисляется по формуле, известной из школьного курса математики:
. Сумма геометрической прогрессии вычисляется по формуле, известной из школьного курса математики:
 . В нашем случае
. В нашем случае 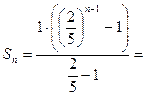
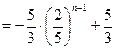 .
.  . Получили конечный предел, поэтому, по определению, ряд сходится.
. Получили конечный предел, поэтому, по определению, ряд сходится.
4. 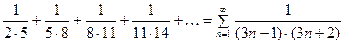 .
.
Общий член этого ряда можем записать в виде суммы элементарных дробей:
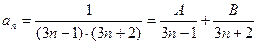 .
.
Отсюда получаем:  , или, приравнивая коэффициенты при одинаковых степенях
, или, приравнивая коэффициенты при одинаковых степенях  в левой и правой частях равенства, получаем:
в левой и правой частях равенства, получаем: 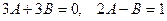 . Сле –довательно,
. Сле –довательно,  и
и 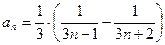 .
.
|
|
|
Тогда частичная сумма данного ряда:
 Тогда сумма ряда
Тогда сумма ряда  - конечное число и ряд сходится.
- конечное число и ряд сходится.
Так как сходимость ряда, по определению, эквивалентна сходимости последовательности частичных сумм, то для этой последовательности можно применить критерий Коши, кото -рый определяет необходимое и достаточное условие сходи –мости: последовательность 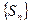 сходится тогда и только тог -да, когда для любого числа
сходится тогда и только тог -да, когда для любого числа 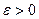 существует номер
существует номер 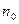 , начиная с которого (т.е. для всех
, начиная с которого (т.е. для всех  ) и для любого натурального числа
) и для любого натурального числа  выполняется неравенс- тво
выполняется неравенс- тво  . Так как разность, стоящая под знаком модуля представляет собой разность двух конечных сумм вида (3) элементов ряда (1), то получаем необжодимый и достаточный признак сходимости ряда (1):
. Так как разность, стоящая под знаком модуля представляет собой разность двух конечных сумм вида (3) элементов ряда (1), то получаем необжодимый и достаточный признак сходимости ряда (1):
ТЕОРЕМА (критерий Коши для ряда) Для того чтобы ряд
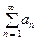 сходился необходимо и достаточно, чтобы для любого
сходился необходимо и достаточно, чтобы для любого 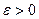 нашелся номер
нашелся номер 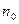 такой, что для всех
такой, что для всех  и любого натурального числа
и любого натурального числа 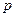 выполнялось неравенство:
выполнялось неравенство:
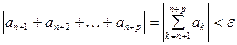 . (4)
. (4)
Обычно, при исследования рядов на сходимость, этим при- знаком не пользуются. Однако он имеет важные следствия.
ОПРЕДЕЛЕНИЕ. Сумма элементов ряда (1) вида:
|
|
|
 (5) называется
(5) называется  - м остатком ряда (1).
- м остатком ряда (1).
Так как в неравенстве (4) число 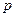 принимает любые натуральные значения, то получаем первое следствие критерия Коши.
принимает любые натуральные значения, то получаем первое следствие критерия Коши.
СЛЕДСТВИЕ 1. Последовательность остатков ряда 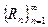 является бесконечно малой последовательностью.
является бесконечно малой последовательностью.
СЛЕДСТВИЕ 2.. (Необходимый признак сходимости ряда)
Если ряд (1) 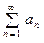 сходится, то общий член этого ряда стремится к нулю, т.е.
сходится, то общий член этого ряда стремится к нулю, т.е. 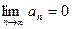 .
.
Этот признак является необходимым, но не достаточным для сходимости ряда. В самом деле, рассмотрим так назы- ваемый гармонический ряд 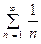 . Предел общего члена этого ряда,
. Предел общего члена этого ряда,  Однако сумма этого ряда бесконечна.
Однако сумма этого ряда бесконечна.
Докажем это, используя критерий Коши. Возьмём 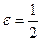 . Если бы ряд сходился, то, для заданного ,
. Если бы ряд сходился, то, для заданного , 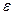 можно было бы найти номер такой, что для всех натуральных
можно было бы найти номер такой, что для всех натуральных 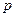 выполнялось бы неравенство:
выполнялось бы неравенство: 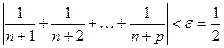 . Однако, при
. Однако, при 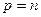 для всех
для всех  получаем следующее неравенство:
получаем следующее неравенство:
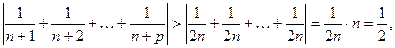
причём это неравенство выполняется для всех  , т.е. не-равенство (4) из условия Коши не выполняется и ряд рас -ходится.
, т.е. не-равенство (4) из условия Коши не выполняется и ряд рас -ходится.
Необходимый признак сходимости чаще используется в другом виде:
Если 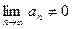 , то ряд (1) расходится.
, то ряд (1) расходится.
Например, ряд 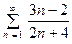 расходится, так как
расходится, так как
|
|
|

СЛЕДСТВИЕ 3. Если сходится ряд 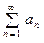 (1), то сходится и ряд
(1), то сходится и ряд 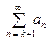 (2), и наоборот, из сходимости ряда (2) следу- ет сходимость ряда (1). Другими словами, на сходимость ряда не влияет отбрасывание конечного числа первых слагаемых или добавление конечного числа слагаемых.
(2), и наоборот, из сходимости ряда (2) следу- ет сходимость ряда (1). Другими словами, на сходимость ряда не влияет отбрасывание конечного числа первых слагаемых или добавление конечного числа слагаемых.
В самом деле, при отбрасывании или добавлении конеч -ного числа слагаемых в ряде (1) частичные суммы получен- ных рядов уменьшаются или увеличиваются на конечное число и, в резкльтате, предел остаётся конечным.
В заключение параграфа приведём ещё алгебраические свойства сходящихся рядов:
1. Если сходится ряд 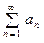 и его сумма равна
и его сумма равна 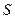 , то сходится и ряд
, то сходится и ряд 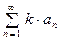 и его сумма равна
и его сумма равна 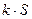 .
.
2. Если  и
и 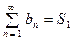 два сходящихся ряда, то
два сходящихся ряда, то
сходятся и ряды 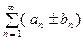 и суммы их равны, соот- ветственно
и суммы их равны, соот- ветственно  .
.
§ 2 ЧИСЛОВЫЕ РЯДЫ С ПОЛОЖИТЕЛЬНЫМИ
ЧЛЕНАМИ. НЕОБХОДИМЫЕ И ДОСТАТОЧНЫЕ
ПРИЗНАКИ СХОДИМОСТИ
В данном параграфе рассматриваем ряды 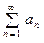 , для которых
, для которых  для всех
для всех  . Для таких рядов последова- тельность частичных сумм является монотонно возрастающей (неубывающей). Поэтому необходимый и достаточный при -знак сходимости таких рядов даёт теорема:
. Для таких рядов последова- тельность частичных сумм является монотонно возрастающей (неубывающей). Поэтому необходимый и достаточный при -знак сходимости таких рядов даёт теорема:
ТЕОРЕМА 1. Для того чтобы ряд с положительными членами сходиля необходимо и достаточно, чтобы последова- тельность его частичных сумм была ограничена.
В самом деле, если ряд сходится, то сходится после -довательность частичных сумм этого ряда, а любая сходя -щаяся последовательность является ограниченной.
С другой стороны, любая монотонная ограниченная после- довательность всегда имеет предел, а если последова- тельность частичных сумм имеет предел, то ряд сходится.
Признаки сравнения рядов. Пусть даны два числовых ряда с положительными членами: 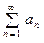 (1) и
(1) и 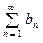 (2).
(2).
Чтобы применять признаки сравнения, корорые будут приведе- ны ниже, нам необходимы знать некоторые сведения о рядах, которые будем выбирать для сравнения.
Во – первых, это известная из школьного курса математики сумма элементов геометрической прогрессии с первым эле -ментом 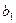 и знаменателем
и знаменателем 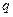 :
:
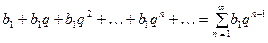 . (3)
. (3)
Частичная сумма этого ряда:
 .
.
Очевидно, что конечный предел этих частичных сумм су- ществует только в случае, если 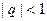 и только при этом условии ряд (3) сходится. Если
и только при этом условии ряд (3) сходится. Если 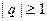 , то данный ряд расхо- дится.
, то данный ряд расхо- дится.
Во – вторых, это так называемый обобщённый гармони -ческий ряд:
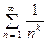 (4)
(4)
Данный ряд сходится при 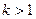 и расходится при
и расходится при 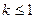 .
.
1. Первый признак сравнения (мажорантный ).
ТЕОРЕМА 2. Пусть даны два числовых ряда с положитель- ными членами 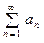 (1) и
(1) и 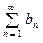 (2). Пусть для всех нату- ральных
(2). Пусть для всех нату- ральных 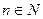 для членов этих рядов выполняются нера -венства:
для членов этих рядов выполняются нера -венства:
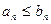 . (5)
. (5)
Тогда, если сходится ряд (2) (с большими членами), то сходится и ряд (1), и наоборот, если расходится ряд (1) (с меньшими членами), то расходится и ряд (2).
В самом деле, для частичных сумм этих рядов выполняют- ся неравенства, аналогичные неравенству (5):
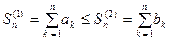 .
.
Известно, что при переходе к пределу знак неравенства сохраняется, т.е. 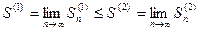 . Если ряд (2) сходится, то получаем неравенство
. Если ряд (2) сходится, то получаем неравенство 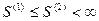 и ряд (1) также сходится, и наоборот, если ряд (1) расходится, то по – лучаем неравенство
и ряд (1) также сходится, и наоборот, если ряд (1) расходится, то по – лучаем неравенство  и ряд (2) также расходит- ся.
и ряд (2) также расходит- ся.
Рассмотрим примеры. Исследовать на сходимость следую- шие ряды:
1. 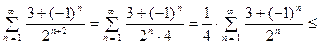 .
.
Судя по виду ряда, можно предположить, что сравнивать его
будем со сходящимся рядом 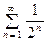 (сумма сходящейся гео- метрической прогрессии). Числитель дроби принимает значе- ние 4 при чётных
(сумма сходящейся гео- метрической прогрессии). Числитель дроби принимает значе- ние 4 при чётных  и 2 при нечётных значениях
и 2 при нечётных значениях  .
.
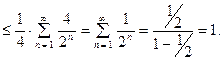
(Сумма бесконечно убывающей геометрической прогрессии равна 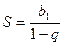 ). Следовательно, исходный ряд сходится.
). Следовательно, исходный ряд сходится.
2. 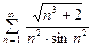 . Учитывая ограниченность функции
. Учитывая ограниченность функции  , можем предположить, что ряд расходится, при данном отношении старших степеней
, можем предположить, что ряд расходится, при данном отношении старших степеней  в числителе и зна- менателе дроби. Если вспомнить, что дробь уменьшается, если уменьшить её числитель и увеличить знаменатель, то по- лучим следующее неравенство:
в числителе и зна- менателе дроби. Если вспомнить, что дробь уменьшается, если уменьшить её числитель и увеличить знаменатель, то по- лучим следующее неравенство:
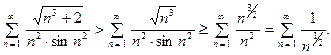
Ряд, стоящий справа - это обобщённый гприонический ряд с 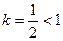 , поэтому он расходится. Поэтому расходится и ис – ходный ряд, элементы которого больше элементов этого ряда.
, поэтому он расходится. Поэтому расходится и ис – ходный ряд, элементы которого больше элементов этого ряда.
Замечание 1. Теорема 2 останется верной, если неравенство (5) выполняется не для всех натуральных значений  , а толь- ко начиная с некоторого номера
, а толь- ко начиная с некоторого номера 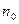 (на сходимость ряда не влияет отбрасывание конечного числа слагаемых).
(на сходимость ряда не влияет отбрасывание конечного числа слагаемых).
Замечание 2. Выводы теоремы 2 остаются верными, если для элементов рядов выполняется неравенство:
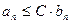 , (6) где
, (6) где 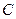
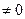 - произвольная постоянная.
- произвольная постоянная.
2. Второй признак сравнения (предельный)
ТЕОРЕМА 3. Пусть даны два ряда со строго положи- тельными членами 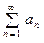 (1) и
(1) и 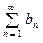 (2), для элементов которых выполняется условие:
(2), для элементов которых выполняется условие:
 . (7)
. (7)
Тогда ряды (1) и (2) ведут себя одинаково, т.е. сходятся и
расходятся одновременно.
В самом деле, из определения предела следует, что для любого 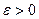 найдётся номер
найдётся номер 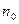 , начиная с которого (т.е. для всех
, начиная с которого (т.е. для всех  ) выполняется неравенство
) выполняется неравенство
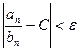 ,
,
Отсюда, 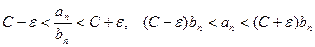 .
.
Учитывая замечание 2 из предыдущей теоремы, из сходимости ряда (2), по неравенству (6), следует сходимость ряда (1), и наоборот, из расходимости ряда (1) следует расходимость ряда (2).
В частности, если 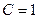 , то равенство (7) означает экви -лентность рядов (1) и (2) (
, то равенство (7) означает экви -лентность рядов (1) и (2) ( 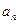 ~
~ 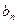 ).
).
Рассмотрим примеры. Исследовать на сходимость ряды:
1.  . Общий член этого ряда
. Общий член этого ряда
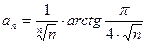 ~
~ 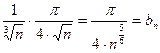 при
при 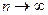 .
.
Тогда 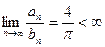 . Ряд
. Ряд 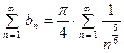 расходится, как
расходится, как
обобщённый гармонический ряд с 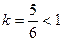 . Тогда расходится и исходный ряд.
. Тогда расходится и исходный ряд.
2. 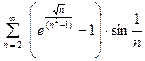 . Для данного ряда, применяя таб- лицу эквивалентных бесконечно малых функций, получим:
. Для данного ряда, применяя таб- лицу эквивалентных бесконечно малых функций, получим:
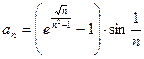 ~
~ 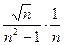 ~
~ 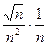 ~
~ 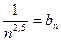 .
.
Ряд 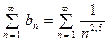 сходится, так как
сходится, так как 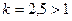 , следо- вательно исходный ряд также сходится, так как предел отно- шения общих членов этих рядов равен 1 (т.к. они эквивалент- ны).
, следо- вательно исходный ряд также сходится, так как предел отно- шения общих членов этих рядов равен 1 (т.к. они эквивалент- ны).
3. Признак Даламбера.
Пусть для элементов ряда 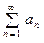 (1) выполняется условие:
(1) выполняется условие:
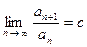 . (8)
. (8)
Тогда, если 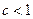 , то ряд (1) сходится; если
, то ряд (1) сходится; если 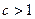 , то ряд (1) расходится; если
, то ряд (1) расходится; если 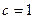 , то данный признак не даёт ответа на вопрос о сходимости ряда.
, то данный признак не даёт ответа на вопрос о сходимости ряда.
В самом деле, из определения предела следует, что для любого 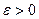 найдётся номер
найдётся номер 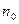 , начиная с которого (т.е. для всех
, начиная с которого (т.е. для всех  ) выполняется неравенство:
) выполняется неравенство: 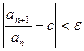 , или, что то же самое
, или, что то же самое
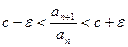 . (9)
. (9)
Пусть 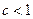 . Выберем
. Выберем 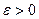 так, чтобы
так, чтобы 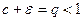 . Тогда
. Тогда
из правой части неравенства (9), получаем 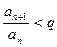 , или
, или  Таким образом, получаем следующее неравенство:
Таким образом, получаем следующее неравенство:
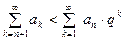 , которое выполняется для всех
, которое выполняется для всех  .
.
Ряд, стоящий справа, представляет собой сумму сходящей- ся геометрической прогрессии (  ). Тогда, по первому при- знаку сравнения, ряд, стоящий в левой части неравенства, также сходится. По следствию 3 из предыдущего параграфа, получаем сходимость ряда (1).
). Тогда, по первому при- знаку сравнения, ряд, стоящий в левой части неравенства, также сходится. По следствию 3 из предыдущего параграфа, получаем сходимость ряда (1).
Пусть 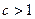 . Выберем
. Выберем 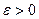 так, чтобы
так, чтобы  . Тогда
. Тогда  , т.е., начиная с номера
, т.е., начиная с номера 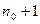 , члены ряда (1) образуют возрастающую последовательность и не выполняется необходимый признак сходимости рядов.
, члены ряда (1) образуют возрастающую последовательность и не выполняется необходимый признак сходимости рядов.
Поэтому ряд (1) расходится.
ПРИМЕРЫ. Исследовать на сходимость ряды:
1. 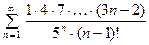 .
.  ,
, 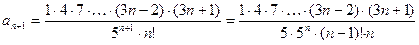 .
.
Тогда получаем:
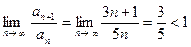 .
.
По признаку Даламбера, ряд сходится.
2.  . Для данного ряда
. Для данного ряда  . Тогда
. Тогда 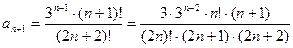 .
.
Применим признак Даламбера:
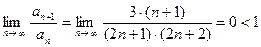
(степень числителя меньше степени знаменателя). Поэтому ряд сходится.
3. 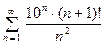 . Здесь
. Здесь 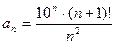 , следователь- но
, следователь- но 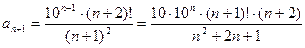 . После сокра-
. После сокра-
щения, получаем: 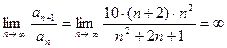
(степень числителя больше степени знаменателя). Следова – тельно данный ряд расходится.
Замечание. Признаком Даламбера удобно пользоваться в случае, если общий член ряда содержит  - ые степени, фак – ториалы, бесконечные произведения.
- ые степени, фак – ториалы, бесконечные произведения.
4. Признак Коши (радикальный)
Пусть для элементов ряда 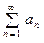 (1) выполняется условие:
(1) выполняется условие:
 . (10)
. (10)
Тогда, если 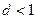 , то ряд (1) сходится; если
, то ряд (1) сходится; если  , то ряд (1) расходится; если
, то ряд (1) расходится; если 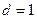 , то данный признак не даёт ответа на вопрос о сходимости ряда.
, то данный признак не даёт ответа на вопрос о сходимости ряда.
В самом деле, равенство (10) означает, что для любого 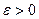 найдётся номер
найдётся номер 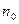 такой, что для всех
такой, что для всех  выпол– няется неравенство
выпол– няется неравенство  , или
, или 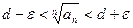 .
.
Пусть 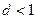 . Выберем
. Выберем 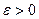 таким образом, чтобы
таким образом, чтобы 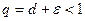 . Тогда, для
. Тогда, для  выполняется неравенство:
выполняется неравенство:
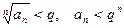 . В этом случае элементы ряда (1) меньше элементов сходящейся геометрической прогрессии и, по первому признаку сравнения, ряд (1) сходится.
. В этом случае элементы ряда (1) меньше элементов сходящейся геометрической прогрессии и, по первому признаку сравнения, ряд (1) сходится.
Если  , выбираем
, выбираем 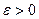 так, чтобы
так, чтобы 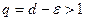 . Тогда
. Тогда 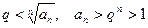 и не выполняется необходимый признак сходимости. Поэтому при данном условии ряд (1) рас- ходится.
и не выполняется необходимый признак сходимости. Поэтому при данном условии ряд (1) рас- ходится.
Чтобы пользоваться признаком Коши при исследовании рядов на сходимость следует знать такие факты:
1)  ; 2)
; 2) 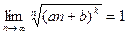 для любых фиксиро -ванных значений
для любых фиксиро -ванных значений 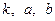 .
.
ПРИМЕРЫ. Исследовать на сходимость ряды:
1. 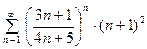 .
.
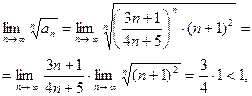
поэтому ряд сходится.
2. 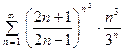 .
.
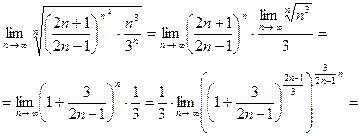
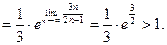
Следовательно, ряд расходится.
Замечание. Радикальный признак Коши чаще всего приме -няется, если общий член ряда содержит  - ые степени, но иногда приходится применять этот признак в случае, если общий член ряда содержит факториал. В этом случае при вычислении корня приходится использовать формулу Стир –линга: при
- ые степени, но иногда приходится применять этот признак в случае, если общий член ряда содержит факториал. В этом случае при вычислении корня приходится использовать формулу Стир –линга: при 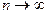 выполнено
выполнено 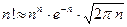 .
.
3. Исследовать на сходимость ряд 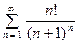 .
.
По признаку Коши:

и, следовательно, данный ряд сходится.
5. Интегральный признак Коши
Пусть дан ряд 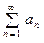 (1). Составим функцию
(1). Составим функцию  таким образом, чтобы для всех натуральных чисел
таким образом, чтобы для всех натуральных чисел  выполнялось равенство
выполнялось равенство  . Если полученная функция является непрерывной, положительной и невозрастающей на промежутке
. Если полученная функция является непрерывной, положительной и невозрастающей на промежутке 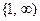 , то выполняется следующее условие:
, то выполняется следующее условие:
Если сходится необственный интеграл
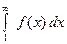 , (11) то сходится и ряд (1), и наоборот, если расходится интеграл (11), то расходится и ряд (1).
, (11) то сходится и ряд (1), и наоборот, если расходится интеграл (11), то расходится и ряд (1).
В самои деле, если 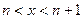 , то, так как функция не- возрастающая,
, то, так как функция не- возрастающая,  . Тогда, по свойству ин- тегралов,
. Тогда, по свойству ин- тегралов, 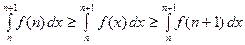 , или
, или
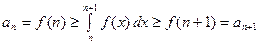 . Суммируем данное не-
. Суммируем данное не-
равенство по  от
от  до
до 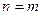 , получим:
, получим:
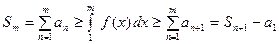 . (12)
. (12)
Перейдём в данном неравенстве к пределу при 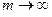 .
.
В правой части неравенства, если интеграл сходится, то 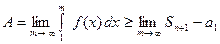 . Предел конечный, поэтому ряд сходится. Если интеграл расходится, то, учитывая левую часть неравенства, получим
. Предел конечный, поэтому ряд сходится. Если интеграл расходится, то, учитывая левую часть неравенства, получим  . Сле- довательно ряд также расходится.
. Сле- довательно ряд также расходится.
С помощью интегрального признака легко устанавливить условия сходимости обобщённого гармонического ряда
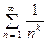 ,
,
которые мы уже использовали, применяя признаки сравнения.
Рассмотрим функцию 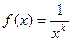 . Она непрерывная, положительная и неубывающая при
. Она непрерывная, положительная и неубывающая при 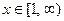 . Можем применить интегральный признак.
. Можем применить интегральный признак.
Пусть 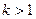 , тогда
, тогда
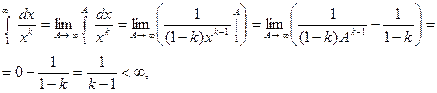 Интеграл сходится, поэтому и ряд сходится.
Интеграл сходится, поэтому и ряд сходится.
При 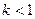
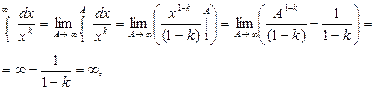
Интеграл расходится, следовательно, ряд также расходится.
Интегральный признак удобно применять в случае, если интеграл хорошо вычисляется.
ПРИМЕРЫ. Исследовать на сходимость ряды:
1.  . Рассмотрим функцию
. Рассмотрим функцию  . Она положительная, убывающая и непрерывна при
. Она положительная, убывающая и непрерывна при 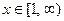 .
.
Тогда
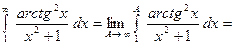
сделаем замену:  при
при 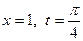 , при
, при 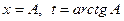 . Получим:
. Получим:
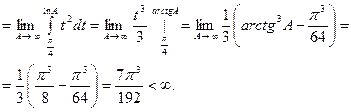
Интеграл сходится, следовательно, и ряд также сходится.
2.  . Соответствующая функция имеет вид:
. Соответствующая функция имеет вид: 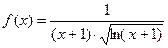 . Она положительная, непрерыв- ная и убывает на промежутке
. Она положительная, непрерыв- ная и убывает на промежутке 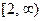 . Исследуем на сходи - мость несобственный интеграл:
. Исследуем на сходи - мость несобственный интеграл:
 сделаем замену переменной:
сделаем замену переменной: 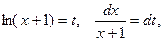
при 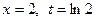 ; при
; при  . Тогда получим:
. Тогда получим:
 .
.
Интеграл расходится, следовательно, и ряд расходится.
§ 3 ЗНАКОПЕРЕМЕННЫЕ РЯДЫ.
Рассмотрим ряд :
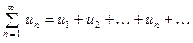 , (1) элементами которого являются произвольные действительные числа. Соответствующий ему ряд из абсолютных величин:
, (1) элементами которого являются произвольные действительные числа. Соответствующий ему ряд из абсолютных величин:
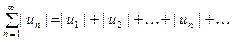 (2)
(2)
ТЕОРЕМА 1. Если сходится ряд (2), составленный из абсо- лютных величин, то сходится и ряд (1).
В самом деле, если ряд (2) сходится, то, по критерию Коши, для любого 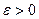 существует номер
существует номер 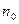 , такой что для всех
, такой что для всех  и всех натуральных значений
и всех натуральных значений 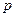 выполняется неравенство
выполняется неравенство
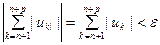 .
.
Тогда для элементов ряда (1) выполняется неравенство:
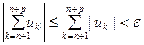 .
.
Следовательно, по критерию Коши, данный ряд сходится.
При этом ряд (1) называется абсолютно сходящимся.
ОПРЕДЕЛЕНИЕ Ряд (1) называется условно сходящимся, если данный ряд сходится, а соответствующий ему ряд (2), составленный из абсолютных величин, расходится.
Частным случаем знакопеременных рядов являются так на- зываемые знакочередующиеся ряды.
Знакочередующимся рядом называется ряд, у которого члены с номерами  и
и  для любых натуральных значе- ний
для любых натуральных значе- ний  имеют противоположные знаки, т.е. ряды вида:
имеют противоположные знаки, т.е. ряды вида:
 , (3) где
, (3) где  .
.
ТЕОРЕМА 2 (признак Лейбница). Знакочередующийся ряд
(3) сходится, если модули его элементов убывают с воз- растанием  , т.е. для всех
, т.е. для всех 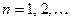 выполняется неравенство
выполняется неравенство  (
(  и выполнен необходимый признак сходимости, т.е.
и выполнен необходимый признак сходимости, т.е. 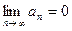
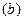 .
.
В самом деле, рассмотрим частичные суммы ряда (3) с четными и нечетными номерами:
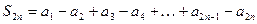 ;
;
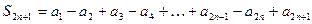 .
.
Преобразуем первую из двух сумм двумя способами:
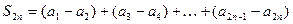 и
и
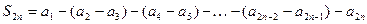 . Учитывая условие
. Учитывая условие  , в первом представлении четных час – тичных сумм каждая скобка является положительной, и поэ- тому последовательность четных частичных сумм является возрастающей. Из второго представления, так как каждая скобка по - прежнему, положительна, следует, что
, в первом представлении четных час – тичных сумм каждая скобка является положительной, и поэ- тому последовательность четных частичных сумм является возрастающей. Из второго представления, так как каждая скобка по - прежнему, положительна, следует, что 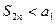 . Любая монотонно возрастающая ограниченная сверху последо- вательность имеет предел, т.е. существует
. Любая монотонно возрастающая ограниченная сверху последо- вательность имеет предел, т.е. существует 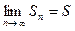 . Так как
. Так как 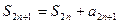 , то учитывая условие
, то учитывая условие 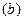 , получим:
, получим: 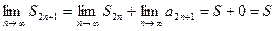 . Следовательно, для всех частичных сумм
. Следовательно, для всех частичных сумм 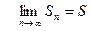 и ряд сходится.
и ряд сходится.
Данная теорема определяет признак сходимости знакопере - менного ряда.
Признак Лейбница. Ряд (1) сходится условно, если выпол- няются два условия: 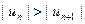 для всех
для всех 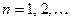 (
(  и
и 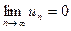
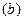 .
.
Рассмотрим несколько примеров исследования знакочереду- ющихся рядов на сходимость.
ПРИМЕРЫ:
1. 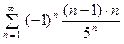 . Соответствующий ряд из абсолют- ных величин
. Соответствующий ряд из абсолют- ных величин 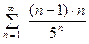 ,
,  ,
, 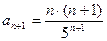 . По признаку Даламбера,
. По признаку Даламбера,
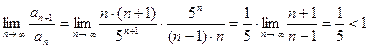 .
.
Ряд из абсолютных величин сходится по признаку Даламбера. Следовательно, исходный ряд сходится абсолютно.
2.  . Ряд из абсолютных величин имеет вид:
. Ряд из абсолютных величин имеет вид:  . Общий член этого ряда
. Общий член этого ряда  . При
. При 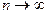
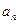 ~
~ 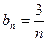 . Ряд
. Ряд 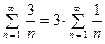 расходится как гар- монический ряд. Поэтому нет абсолютной сходимости исход- ного ряда. Проверяем условную сходимость данного ряда по признаку Лейбница. Условие
расходится как гар- монический ряд. Поэтому нет абсолютной сходимости исход- ного ряда. Проверяем условную сходимость данного ряда по признаку Лейбница. Условие  : подставляя
: подставляя 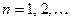 в
в 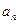 , получаем неубывающую цепочку
, получаем неубывающую цепочку 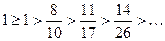 и условие
и условие 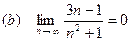 . Следовательно, ряд сходится условно.
. Следовательно, ряд сходится условно.
3. 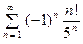 . Ряд из абсолютных величин
. Ряд из абсолютных величин 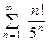 . По признаку Даламбера,
. По признаку Даламбера,
 .
.
Следовательно, нет абсолютной сходимости исходного ряда.
Проверим выполнение условия 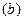 признака Лейбница , исполь- зуя формулу Стирлинга,
признака Лейбница , исполь- зуя формулу Стирлинга,
 . Тогда ряд расходится, так как не выполнен необходимый при -знак сходимости ряда. (при
. Тогда ряд расходится, так как не выполнен необходимый при -знак сходимости ряда. (при  и
и 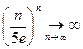 ).
).
В заключение параграфа, приведём ещё одну теорему, ко- торая имеет важное значение в приложениях теории рядов для приближённых вычислений.
ТЕОРЕМА 3. Сумма остатка знакочередующего ряда, удо- влетворяющего условию Лейбница: 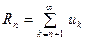 удовлетворя -ет следующему условию :
удовлетворя -ет следующему условию : 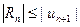 и её знак совпадает со знаком
и её знак совпадает со знаком 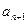 .
.
Теорему доказывать не будем. Рассмотрим пример: вы -числить сумму ряда 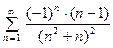 с точностью
с точностью 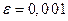 .
.
Учитывая теорему 3, есть смысл записывать слагаемые до тех пор, пока очередное слагаемое по модудю не станет меньше 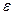 . Это будет означать, что сумма остатка ряда будет меньше
. Это будет означать, что сумма остатка ряда будет меньше 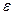 и получим нужную точность вычисления.
и получим нужную точность вычисления.
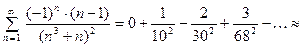
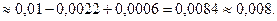
2. ЭЛЕМЕНТЫ ФУНКЦИОНАЛЬНЫХ РЯДОВ.
§ 1. ОПРЕДЕЛЕНИЕ ФУНКЦИОНАЛЬНОГО РЯДА
Задание функционального ряда от некоторой переменной  состоит в задании последовательности функций от этой переменной, являющимися членами функционального ряда. Другими словами, каждому натуральному числу
состоит в задании последовательности функций от этой переменной, являющимися членами функционального ряда. Другими словами, каждому натуральному числу 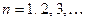 по определённому закону ставится в соответствие некоторая функция
по определённому закону ставится в соответствие некоторая функция  . Множество этих функций, заданных на одном и том же множестве
. Множество этих функций, заданных на одном и том же множестве 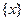 , которое является областью опре -деления этих функций:
, которое является областью опре -деления этих функций: 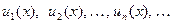 , называется функциональной последовательностью.
, называется функциональной последовательностью.
ОПРЕДЕЛЕНИЕ. Выражение
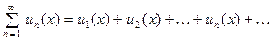 (1)
(1)
называется функциональным рядом относительно перемен- ной  .
.
Придавая в выражении (1) переменной  различные фик- сированные числовые значения, будем получать числовые ря- ды, которые могут оказаться сходящимися или расходящимися.
различные фик- сированные числовые значения, будем получать числовые ря- ды, которые могут оказаться сходящимися или расходящимися.
ОПРЕДЕЛЕНИЕ. Множество всех значений переменных  , при которых ряд окахывается сходящимся, называется об- ластью сходимости функционального ряда.
, при которых ряд окахывается сходящимся, называется об- ластью сходимости функционального ряда.
ПРИМЕРЫ:
1.  .
.
Данный ряд представляет собой геометрическую прогрессию со знаменателем  , который сходится при
, который сходится при 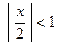 . Поэтому область сходимости данного ряда:
. Поэтому область сходимости данного ряда: 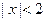 .
.
2. 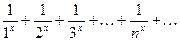 .
.
Это обобщённый гпрмонический ряд, который сходится при 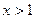 . Поэтому множество
. Поэтому множество 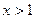 представляет собой область
представляет собой область
сходимости данного ряда.
Если некоторое число 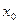 входит в область сходимости
входит в область сходимости 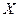 функционального ряда, то есть смысл говорить о сумме функционального ряда в данной точке.
функционального ряда, то есть смысл говорить о сумме функционального ряда в данной точке.
Частичной суммой ряда (1) в точке 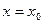 называется сумма вида:
называется сумма вида:
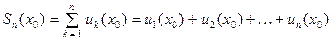 , (2) а суммой ряда в данной точке называется предел частичных сумм:
, (2) а суммой ряда в данной точке называется предел частичных сумм:  .
.
Таким образом, сумма функционального ряда (1) - это функция переменной  , область определения которой совпа-
, область определения которой совпа-
дает с областью сзодимости данного ряда.
Критерий Коши сходимости функционального ряда: Для того чтобы функциональный ряд (1) был сходящимся в области 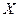 , необходимо и достаточно, чтобы для любого
, необходимо и достаточно, чтобы для любого 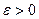 и любого
и любого 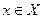 можно было бы найти номер
можно было бы найти номер  такой, что для всех
такой, что для всех 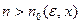 и для всех натуральных
и для всех натуральных 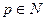 выполнялось бы неравенство:
выполнялось бы неравенство:
 . (3)
. (3)
В частности, для остатка сходящегося в области 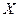 ряда (1) из этого критерия при
ряда (1) из этого критерия при  следует оценка:
следует оценка:
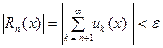 , (4) в случае, если
, (4) в случае, если 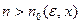 .
.
Сходящийся в области 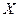 функциональный ряд называется равномерно сходящимся в данной области, если для любого
функциональный ряд называется равномерно сходящимся в данной области, если для любого
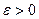 существует, не зависящий от
существует, не зависящий от 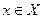 , номер
, номер 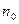 , та -кой, что для всех
, та -кой, что для всех  для остатка ряда (1)
для остатка ряда (1)
 (5)
(5)
выполняется оценка 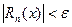 для всех
для всех 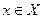 .
.
Для равномерной сходимости ряда (1) также имеет место критерий Коши, только в условии критерия номер 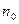 не зависит от
не зависит от  и неравенство (3) выполняется для всех
и неравенство (3) выполняется для всех 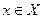 .
.
Замечание. Равномерная сходимость функционального ряда равносильна равномерной сходимости его частичных сумм.
Проверка выполнения критерия Коши затруднительна даже для числовых рядов. Эффективный способ проверки равномер- ной сходимости функционального ряда представляет собой признак Вейерштрасса.
ТЕОРЕМА 1. (признак Вейерштрасса равномерной схо – димости). Если положительный числовой ряд 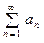 сходит –ся и для всех членов функционального ряда
сходит –ся и для всех членов функционального ряда 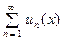 (1) имеет место оценка:
(1) имеет место оценка:
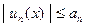 для всех
для всех 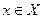 и всех
и всех  , (6) то ряд (1) сходится равномерно в области
, (6) то ряд (1) сходится равномерно в области 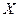 . При этом ряд (1) называется мажорируемым в области
. При этом ряд (1) называется мажорируемым в области 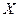 .
.
В самом деле, учитывая условия (6) и сходимость ряда
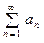 , получаем:
, получаем:
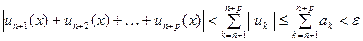 для
для  и всех
и всех 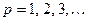 .
.
Это означает, что выполнен критерий Коши равномерной схо- димости и ряд (1) является равномерно сходящимся в об -ласти .  .
.
ПРИМЕР. Проверить равномерную сходимость на отрезке 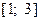 ряда
ряда 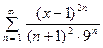 , используя признак Вейерштрасса.
, используя признак Вейерштрасса.
Для всех  и всех
и всех 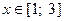 для элементов данного ряда выполняется неравенство:
для элементов данного ряда выполняется неравенство:
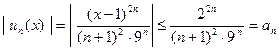 .
.
Исследуем ряд 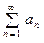 на сходимость по признаку Даламбера
на сходимость по признаку Даламбера
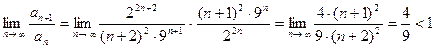 Данный ряд сходится. Следовательн исходный ряд сходится равномерно.
Данный ряд сходится. Следовательн исходный ряд сходится равномерно.
ТЕОРЕМА 2. Пусть все члены функционального ряда (1)
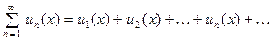 определены и непрерывны на промежутке
определены и непрерывны на промежутке 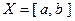 и сос- тавленный из них функциональный ряд равномерно сходится. Тогда сумма данного ряда - функция, непрерывная на том же промежутке.
и сос- тавленный из них функциональный ряд равномерно сходится. Тогда сумма данного ряда - функция, непрерывная на том же промежутке.
Из непрерывности членов функционального ряда следует непрерывность каждой из её частичных сумм:
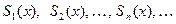 .
.
По условию, эта последовательность равномерно сходится на промежутке 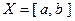 . Следовательно, сумма ряда - функ- ция
. Следовательно, сумма ряда - функ- ция 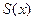 также непрерывна на этом промежутке.
также непрерывна на этом промежутке.
Без доказательства приведём ещё две теоремы.
ТЕОРЕМА 3 (о почленном интегрировании рядов). Если функциональный ряд 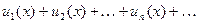 сходится равномерно на некотором промежутке
сходится равномерно на некотором промежутке 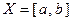 и его сум- ма равна
и его сум- ма равна 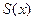 , то для любого промежутка
, то для любого промежутка 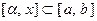 функциональный ряд (относительно
функциональный ряд (относительно  ) из интегралов
) из интегралов
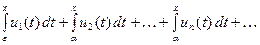
также сходится равномерно на том же промежутке и его сумма равна  (т.е. равномерно сходящиеся функци- ональные ряды можно почленно интегрировать).
(т.е. равномерно сходящиеся функци- ональные ряды можно почленно интегрировать).
ПРИМЕР. Рассмотрим функциональный ряд:
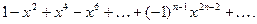
Данный ряд представляет собой геометрическую прогрессию, которая равномерно сходится при 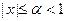 . Его сумма
. Его сумма
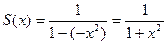 .
.
После интегрирования получаем:
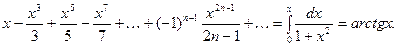 . (7)
. (7)
ТЕОРЕМА 4 (о почленном дифференцировании рядов). Пусть ряд 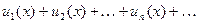 (1) сходится на промежутке
(1) сходится на промежутке 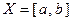 , имеет сумму
, имеет сумму 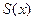 и его члены име- ют на этом промежутке непрерывные производные, причём составленный из этих производных ряд
и его члены име- ют на этом промежутке непрерывные производные, причём составленный из этих производных ряд
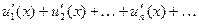 (8)
(8)
равномерно сходится и его сумма равна 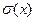 .
.
Тогда ряд (1) также равномерно сходится на том же про- межутке и его производная его суммы равна сумме ряда (8):
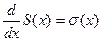 , т.е. равномерно сходящиеся функциональные ряды можно почленно дифференцировать.
, т.е. равномерно сходящиеся функциональные ряды можно почленно дифференцировать.
ПРИМЕР. Вспомним известное разложение в ряд функции:
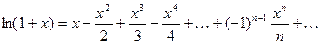 , который, очевидно, сходится равномерно при
, который, очевидно, сходится равномерно при 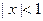 . Тогда, применяя теорему, получим:
. Тогда, применяя теорему, получим:
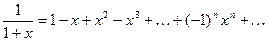 .
.
§ 2 СТЕПЕННЫЕ РЯДЫ.
ОПРЕДЕЛЕНИЕ. Степенным рядом называется функцио – нальный ряд вида:
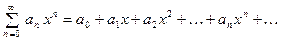 , (1)
, (1)
где 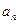 - действительные числа, которые называются коэф – фициентами ряда. Степенным рядом можно назвать также ряд
- действительные числа, которые называются коэф – фициентами ряда. Степенным рядом можно назвать также ряд 
(2)
Следует заметить, что всякий степенной ряд вида (1) всег- да сходится в точке 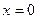 (а ряд вида (2) - в точке
(а ряд вида (2) - в точке 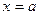 ). Поэтому область сходимости степенного ряда всегда является непустым множеством.
). Поэтому область сходимости степенного ряда всегда является непустым множеством.
Чтобы определить вид области сходимости степенного ря- да, докажем следующую теорему:
ТЕОРЕМА 1 (Абеля о сходимости степенного ряда).
1. Пусть степенной ряд (1) сходится в точке 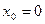 . Тогда он сходится в любой точке
. Тогда он сходится в любой точке  , удовлетворяющей нера- венству
, удовлетворяющей нера- венству 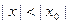 (причём абсолютно).
(причём абсолютно).
2. Если степенной ряд (1) расходится в некоторой точке 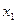 , то он расходится и для всех
, то он расходится и для всех  , удовлетворяющих нера -венству
, удовлетворяющих нера -венству 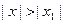 .
.
Докажем эту теорему.
1. По условию, ряд 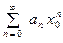 сходится, следовательно, по необходимому признаку сходимости,
сходится, следовательно, по необходимому признаку сходимости,  . Но любая сходящаяся последовательность ограничена. Поэтому сущест- вует некоторое число
. Но любая сходящаяся последовательность ограничена. Поэтому сущест- вует некоторое число  , такое что для всех
, такое что для всех 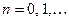 выполняется неравенство:
выполняется неравенство:
 . (3)
. (3)
Ряд (1) можем записать в виде:
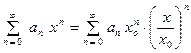 .
.
Так как, по предположению, 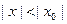 , то получаем нера- венство:
, то получаем нера- венство:
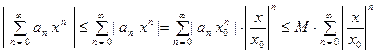 .
.
Сумма ряда 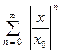 - это сумма геометрической прогрессии с
- это сумма геометрической прогрессии с 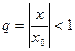 . Данный ряд сходится. Поэтому сходится и ряд
. Данный ряд сходится. Поэтому сходится и ряд
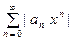 , следовательно, ряд (1) сходится абсолютно.
, следовательно, ряд (1) сходится абсолютно.
2. Докажем от противного. Пусть ряд (1) сходится при некотором значении  . Тогда, как только что было доказано, он должен сходиться и для всех
. Тогда, как только что было доказано, он должен сходиться и для всех 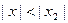 , т.е. и для
, т.е. и для 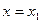 . Получаем противоречие с предположением тео- ремы. Следовательно, ряд расходится для всех
. Получаем противоречие с предположением тео- ремы. Следовательно, ряд расходится для всех 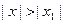 .
.
Из теоремы Абеля можем сделать заключение о виде об- ласти сходимости степенного ряда.
ОПРЕДЕЛЕНИЕ, Радиусом сходимости степенного ряда называется некоторое число 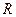 такое, что для всех
такое, что для всех  , удов- летворяющих неравенству
, удов- летворяющих неравенству  , ряд сходится, а для всех
, ряд сходится, а для всех
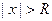 ряд расходится.
ряд расходится.
Значение радиуса сходимости можно определить, используя известные признаки сходимости положительных числовых рядов.
Используя признак Даламбера, радиус сходимости можно найти следующим обраом: пусть 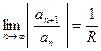 . Тогда
. Тогда
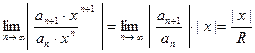 .
.
По признаку Даламбера, ряд сходится, если предел данного отношения меньше 1. Следовательно, сходится при  и расходится при
и расходится при 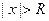 . Тогда радиус сходимости определяет- ся формулой
. Тогда радиус сходимости определяет- ся формулой
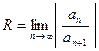 . (4)
. (4)
Аналогичным образом, используя радикальный признак Ко –ши, получаем ещё одно выражение для радиуса сходимости степенного ряда:
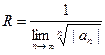 . (5)
. (5)
Если  , то степенной ряд сходится только в одной точке
, то степенной ряд сходится только в одной точке 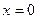 для ряда (1), или, при
для ряда (1), или, при 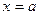 для ряда (2).
для ряда (2).
ПРИМЕРЫ:
1. Найти область сходимости ряда: 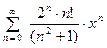 .
.
Для этого ряда, 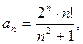
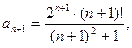 Тогда
Тогда
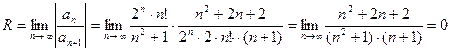
и ряд сходится только в точке 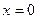 .
.
2. Найти область сходимости ряда: 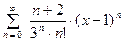 .
.
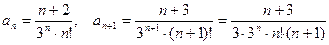 . Тогда
. Тогда
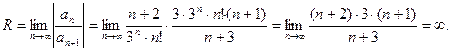
Следовательно, ряд сходится на всей числовой прямой  .
.
ЗАМЕЧАНИЕ 1. В интервале сходимости, т.е. при  степенной ряд сходится абсолютно. Если
степенной ряд сходится абсолютно. Если  или
или 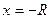 ряд может сходиться или расходиться, поэтому требуется дополнительное исследование ряда на сходимость в этих точках.
ряд может сходиться или расходиться, поэтому требуется дополнительное исследование ряда на сходимость в этих точках.
ЗАМЕЧАНИЕ 2. Пусть степенной ряд имеет радиус сходи -мости 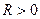 , тогда для любого
, тогда для любого  , удовлетворяющего неравенству
, удовлетворяющего неравенству 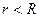 , степенной ряд (1) равномерно сходится для всех
, степенной ряд (1) равномерно сходится для всех 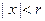 . (получается как следствие теоремы Вейерштрасса.). Отсюда получаем следующее следствие:
. (получается как следствие теоремы Вейерштрасса.). Отсюда получаем следующее следствие:
СЛЕДСТВИЕ. Сумма степенного ряда яаляется непрерывной функцией внутри промежутка сходимости.
Учитывая замечание 2 и теоремы предыдущего параграфа, получаем следующие теоремы.
ТЕОРЕМА 2. Если степенной ряд (1) имеет радиус схо -димости 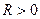 и
и  , то данный ряд можно почленно интегрировать по промежутку
, то данный ряд можно почленно интегрировать по промежутку 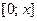 , т.е.
, т.е.
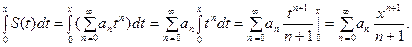
При этом полученный ряд имеет тот же радиус сходимости.
ТЕОРЕМА 3. Если степенной ряд (1) имеет радиус схо -димости 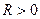 и
и  , то данный ряд можно почленно дифференцировать внутри промежутка сходимости, т.е.
, то данный ряд можно почленно дифференцировать внутри промежутка сходимости, т.е.
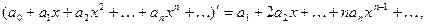 причём полученный ряд имеет тот же радиус сходимости
причём полученный ряд имеет тот же радиус сходимости 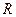 .
.
ЗАМЕЧАНИЕ. Степенной ряд внутри его промежутка сходимости можно дифференцировать почленно сколько угодно раз, причём ряды, полученные в результате дифференцирова– ния, имеют тот же интервал сходимости, что и исходный ряд.
Обычно нет смысла специально находить радиус сходимос -ти степенногл ряда. Область сходимости ряда непосредст- венно получается из неравенств:
 (а), или
(а), или 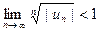 . (б) (6)
. (б) (6)
Рассмотрим несколько примеров.
1. Найти область сходимости ряда: 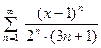 .
.
Для данного ряда 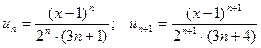 .
.
Тогда область сходимости:
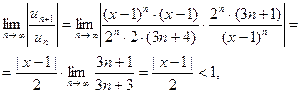
или 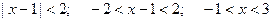 . В данном про –межутке ряд сходится абсолютно. Исследуем сходимость ряда на границах этого промежутка.
. В данном про –межутке ряд сходится абсолютно. Исследуем сходимость ряда на границах этого промежутка.
Пусть  . Тогда из исходного ряда получаем числовой ряд
. Тогда из исходного ряда получаем числовой ряд 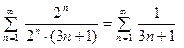 ~
~  . В правой части
. В правой части
стоит гармоничесуий ряд, о котором известно, что он расхо – дится. Следовательно, данный ряд расходится при  .
.
Пусть  . Тогда ряд имеет вид:
. Тогда ряд имеет вид:
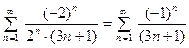 .
.
Получили знакопеременный ряд, который, как было проверено выше, не имеет абсолютной сходимости. Проверим выполне -ние условий признака Лейбница:
(1) 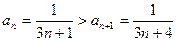 для всех
для всех 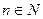 ;
;
(2) 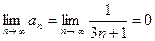 .
.
Таким образом, по признаку Лейбница, в точке  ряд сходится условно, и область сходимости данного ряда
ряд сходится условно, и область сходимости данного ряда 
2. Найти область сходимости ряда 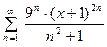 .
.
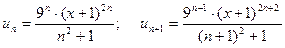 .
.
Тогда область сходимости:
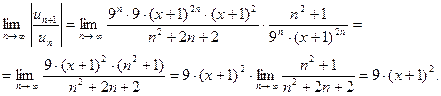
Область сходимости определяется следующим образом:
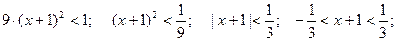
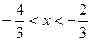 . Исследуем ряд на сходимость на границе области.
. Исследуем ряд на сходимость на границе области.
Пусть 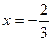 . Тогда получаем ряд:
. Тогда получаем ряд:
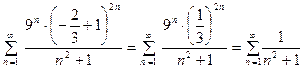 ~
~  .
.
Ряд, стоящий справа, сходится, как обобщённый гармоничес -кий ряд со степенью 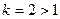 . Тогда сходится и ряд, стоя -щий слева.
. Тогда сходится и ряд, стоя -щий слева.
При 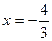 получаем такой же ряд:
получаем такой же ряд:
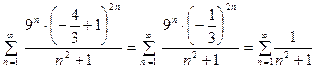 ~
~  и ряд также сходится. Поэтому область сходимости данного ряда:
и ряд также сходится. Поэтому область сходимости данного ряда: 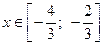 .
.
3. Найти область сходимости ряда 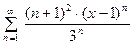 .
.
По формуле (6) б, область сходимости имеет вид:
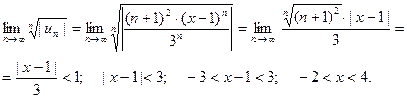
Исследуем сходимость ряда в граничных точках.
Пусть 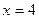 . Тогда получаем ряд
. Тогда получаем ряд
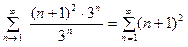 .
.
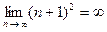 . Поэтому ряд расходится.
. Поэтому ряд расходится.
При 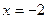 ряд имеет вид:
ряд имеет вид:
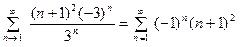 .
.
Данный знакочередующийся ряд расходится, так как не вы -полнено второе условие признака Лейбница: 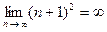 .
.
Следовательно, область сходимости ряда  .
.
§ 3. РЯД ТЕЙЛОРА. ПРИЛОЖЕНИЯ СТЕПЕННЫХ
РЯДОВ В ПРИБЛИЖЁННЫХ ВЫЧИСЛЕНИЯХ.
Пусть  - некоторая функция, имеющая непрерывные производные произвольного порядка.
- некоторая функция, имеющая непрерывные производные произвольного порядка.
Предположим, что в интервале  функцию
функцию  можно разложить в ряд по степеням
можно разложить в ряд по степеням 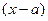 , т.е.
, т.е.
 (1)
(1)
Выразим коэффициенты этого ряда через значения функции и её производных.
Продифференцируем этот ряд в интервале сходимости  раз. Получаем:
раз. Получаем: 
При 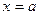 имеем:
имеем:
 Таким образом, получаем следующие коэффициенты ряда (1):
Таким образом, получаем следующие коэффициенты ряда (1):
 Подставив эти выражения в формулу (1), получим:
Подставив эти выражения в формулу (1), получим:
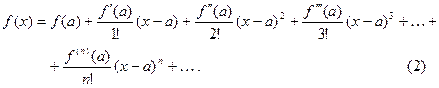
Ряд, стоящий в правой части данного равенства, называет -ся рядом Тейлора для функции  .
.
В частности, в случае 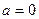 , получаем так называемый ряд Маклорена:
, получаем так называемый ряд Маклорена:
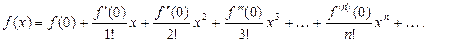
ЗАМЕЧАНИЕ. Необходимые и достаточные условия возмож - ности представления функции  в виде степенного ряда задаёт теорема Тейлора, которая рассматривалась в разделе дифференциального исчисления функции одной переменной.
в виде степенного ряда задаёт теорема Тейлора, которая рассматривалась в разделе дифференциального исчисления функции одной переменной.
ПРИМЕР. Написать разложение по степеням 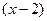 функции:
функции:
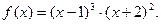
В данном примере 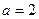 . Преобазуем функцию, раскрыв скобки:
. Преобазуем функцию, раскрыв скобки:

Найдём производные:

Все остальные производные равны нулю. Поэтому получаем следующий ряд :
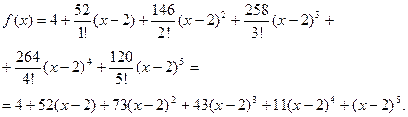
Разложения в ряды Тейлора (Маклорена)
основных элементарных функций.
1. 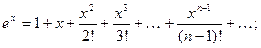
2. 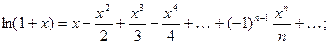
3. 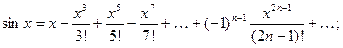
4. 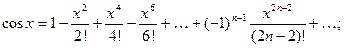
5. 
 ;
;
В частности,

6. 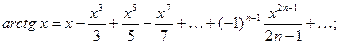
7. 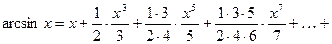
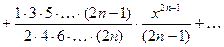 .
.
Интервалы сходимости данных рядов легко найти с помощью обычных методов.
Используя данные разложения, можем получить разложения в ряды Маклорена и других функций.
Например, разложение в степенной ряд функции 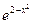 име -ет вид
име -ет вид
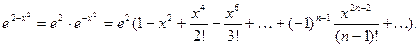
ПРИЛОЖЕНИЯ СТЕПЕННЫХ РЯДОВ.
ПРИМЕРЫ.
Дата добавления: 2021-03-18; просмотров: 60; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
