Для самостоятельного решения.
| B, Тл |
| 0,2 |
| 0,1 |
| 0 |
| 1 |
| 2 |
| 3 |
| 4 |
| t, с |
| Рис. 41 |
12.4. Проводящая квадратная рамка с длиной стороны 10 см помещена в однородное магнитное поле, линии индукции которого составляют угол 60° с направлением нормали к рамке. Определите модуль индукции магнитного поля, если известно, что при его равномерном исчезновении за время 0,02 с в рамке индуцируется э. д. с., равная 10 мВ. (0,04 Тл)
| Рис. 42 |
)
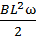12.6. В катушке при силе тока 10 А возникает магнитный поток 5 Вб. Чему равна энергия магнитного поля этой катушки? (25 Дж).
12.7. Катушка с железным сердечником имеет индуктивность, равную 0,5 Гн, при силе тока в ее витках 5 А. Магнитная проницаемость материала сердечника при этих условиях равна 1000. Чему стала равна индуктивность катушки после удаления из нее сердечника? (500 мкГн).
|
|
|
Контрольные вопросы.
12.1. В чем заключается явление электромагнитной индукции?
12.2. Что является причиной возникновения э. д. с. индукции в замкнутом проводящем контуре?
12.3. От чего и как зависит э. д. с. электромагнитной индукции?
12.4. Правило Ленца.
12.5. В чем заключается явление самоиндукции?
12.6. В чем заключается физический смысл индуктивности контура? От чего она зависит? В чем измеряется?
12.7. Энергия магнитного поля.
ЧАСТЬ ЧЕТВЕРТАЯ
КОЛЕБАНИЯ И ВОЛНЫ
Колебаниями называются движения или процессы, которые характеризуются определенной повторяемостью во времени. Вообще колебаниями называется любой периодически повторяющийся процесс, например, движение маятника в часах, смена времен года на планете или движение тела, закрепленного на пружине и т. д. В разных физических явлениях колеблющаяся величина может меняться по различным законам. Но наиболее простым законом является гармонический, то есть закон, при котором колеблющаяся величина меняется по закону синуса или косинуса. Различные колебательные процессы описываются одинаковыми характеристиками и одинаковыми уравнениями.
Колебания называются свободными (или собственными), если они совершаются за счет первоначально сообщенной энергии при последующем отсутствии внешних воздействий на колебательную систему. Простейшим типом колебаний являются гармонические колебания ‑ колебания, при которых колеблющаяся величина изменяется по закону синуса (косинуса).
|
|
|
Колебания, происходящие без влияния внешних сил, называют свободными. Амплитуда таких колебаний не изменяется с течением времени и их называют незатухающими. Рассмотрение гармонических колебаний важно по двум причинам: 1) колебания, встречающиеся в природе и технике, часто имеют характер, близкий к гармоническому; 2) любой периодический процесс (процесс, повторяющийся через равные промежутки времени) можно представить в виде суммы гармонических колебаний.
ГЛАВА 13: Гармонические колебания.
| 0 |
| x |
| Fупр |
| m |
| k |
| Рис. 43 |
|
|
|
.
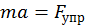Учитывая в данном уравнении (1.2) и (1.4) вместо ускорения a и (2.5) вместо силы упругости, получим
,
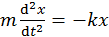знак « ‑ » ставится из-за того, что проекция силы упругости и координата x имеют противоположные знаки. Разделим обе части уравнения на m и перенесем слагаемые в левую часть
.
Обозначим постоянный множитель одной буквой
. (13.1)
Получившееся уравнение:
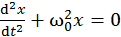, (13.2)
называют дифференциальным (то есть содержащим производную) уравнением гармонических колебаний.
В отличие от алгебраических уравнений, где решением является число, решением дифференциального уравнения является функция. В данном случае решением является зависимость x(t) вида:
. (13.3)
Так ли это, легко проверить, дважды взяв производную от выражения (13.3) и подставив в (13.2). Здесь x – координата тела (отклонение от положения равновесия), A – амплитуда колебаний, то есть максимальное отклонение тела от положения равновесия, 
‑ фаза колебаний, безразмерная величина, характеризующая положение тела в данный момент времени t,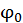 
‑ начальная фаза колебаний, величина, характеризующая положение тела в начальный момент времени t0.
|
|
|
Время, за которое тело совершает одно полное колебание (или фаза колебаний получает приращение 2π), называется периодом колебаний T. Очевидно 
. Величину, обратную периоду, называют линейной частотой колебаний ν, по своему смыслу это количество полных колебаний, совершаемых телом в единицу времени
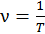. (13.4)
Размерностью частоты является 1/с = Гц (герц). Величину, которую мы обозначили ω0, называют циклической (круговой) частотой колебаний. Из (13.1) следует, что для пружинного маятника циклическая частота представляет собой количество колебаний за 2π секунд и равна
. (13.5)
С учетом этого используя (13.4) можно записать:
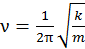и 
. (13.6)
Продифференцировав по времени уравнение колебаний (13.3), получим выражение для мгновенной скорости тела
| x |
| V |
| a |
| t |
| t |
| t |
| +A |
| ‑A |
| +Aω0 |
| ‑Aω0 |
| +Aω02 |
| ‑Aω02 |
| T |
| T |
| T |
| 2T |
| 2T |
| 2T |
| Рис. 44 |
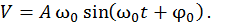(13.7)
Здесь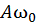 
имеет смысл амплитуды (максимального значения) скорости.
Проделав эту операцию еще раз, получим выражение для ускорения тела
. (13.8)
Здесь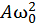 
имеет смысл амплитуды (максимального значения) ускорения. Значит, величины скорости и ускорения тела колеблются с той же циклической частотой. Фазы скорости и смещения отличаются на 
, фазы ускорения и смещения на π. Следовательно, в момент, когда x =0, скорость имеет наибольшие положительные значения, когда же x достигает максимального отрицательного значения, то ускорение приобретает наибольшее положительное значение (рис. 44).
Сила упругости, под действием которой происходят колебания, по второму закону Ньютона равна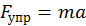 
и, значит, с учетом (13.8),
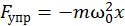. (13.9)
Эта сила всегда направлена в сторону положения равновесия, поэтому ее называют возвращающей. Она прямо пропорциональна смещению тела из положения равновесия. В общем случае, если движение тела происходит под действием силы, удовлетворяющей этим условиям, оно представляет собой гармонические колебания.
Кинетическая энергия материальной точки, совершающей прямолинейные гармонические колебания, равна
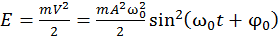. (13.10)
Потенциальная энергия упругой деформации пружины
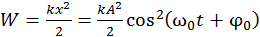. (13.11)
Суммируя эти выражения с учетом (13.1), получим полную механическую энергию пружинного маятника
. (13.12)
Полная энергия остается постоянной, так как при колебаниях справедлив закон сохранения механической энергии, поскольку сила упругости консервативна.
| m |
| L |
| α |
mg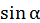 
|
| Рис. 45 |
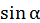. При малых углах отклонения нити от вертикали (можно считать 
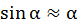) эта сила прямо пропорциональна смещению от положения равновесия, роль которого выполняет угол 
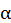. Значит, математический маятник будет совершать гармонические колебания по закону, аналогичному (13.3)
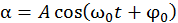. (13.13)
Здесь амплитудой A является максимальный угол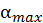 
отклонения нити от вертикали, циклической частотой
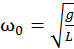, (13.14)
где g – ускорение свободного падения. Период колебаний математического маятника
. (13.15)
Все остальные выводы и терминология, относящиеся к пружинному маятнику, также справедливы и для математического, учитывая изменившийся физический смысл величин. Например, вместо потенциальной энергии силы упругости присутствует потенциальная энергия силы тяжести и т. п.
Гармонические колебания удобно изображать графически методом вращающегося вектора амплитуды, или методом векторных диаграмм. Для этого из произвольной точки O, выбранной на оси x, под углом φ0, равным начальной фазе колебания, откладывается вектор 
, модуль которого равен амплитуде A рассматриваемого колебания (рис. 46). Если этот вектор вращается с угловой скоростью ω0, то проекция конца вектора на ось x будет меняться и принимать значения от – A до + A по закону . Таким образом, гармоническое колебание можно представить изменением проекции на некоторую произвольно выбранную ось вектора амплитуды , отложенного от произвольной точки оси под углом φ0, равным начальной фазе, и вращающегося с угловой скоростью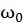 
вокруг этой точки, численно равной циклической частоте колебаний.
| α |
| x |
| O |
| x |
|
|
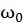
| A |
| Рис. 46 |
Среди различных электрических явлений особое место занимают электромагнитные колебания, при которых электрические величины (заряды, токи) периодически изменяются и которые сопровождаются взаимными превращениями электрического и магнитного полей. Электромагнитные колебания осуществляются в колебательном контуре – цепи, состоящей из включенных последовательно катушки индуктивностью L и конденсатора емкостью C (рис. 47). Такой контур не обладает активным сопротивлением R и поэтому называется идеальным.
Идеальный колебательный контур представляет собой замкнутую цепь, равновесие которой означает электронейтральность всех ее участков. Следовательно, отклонение от положения равновесия состоит в смещении положительных зарядов относительно отрицательных. Это произойдет, если зарядить конденсатор. Но в цепи, состоящей из одного только конденсатора, колебания невозможны, так как такая цепь не обладает инерционностью. Поэтому последовательно с конденсатором подключают катушку индуктивности, в которой ток не может сразу прекратиться, так как в ней возникает э. д. с. самоиндукции.
| C |
| L |
| Рис. 47 |
. После замыкания конденсатора на катушку индуктивности он начинает разряжаться, и в контуре потечет возрастающий со временем ток I и в катушке возникнет магнитное поле. В результате энергия электрического поля будет уменьшаться, а энергия магнитного поля катушки (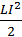 
) – возрастать.
Так как R = 0, то, согласно закону сохранения энергии, полная энергия
,
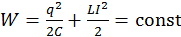так как теплота в цепи не выделяется. Поэтому в момент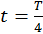 
, когда конденсатор полностью разрядится, энергия электрического поля обращается в нуль, а энергия магнитного поля (а, следовательно, и ток) достигает наибольшего значения. Начиная с этого момента 
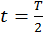, ток в контуре будет убывать, следовательно, начнет ослабевать магнитное поле катушки, и в ней индуцируется ток, который течет (согласно правилу Ленца) в том же направлении, что и ток разрядки конденсатора. Конденсатор начнет перезаряжаться, возникнет электрическое поле, стремящееся ослабить ток, который, в конце концов, обратится в нуль, а заряд на обкладках конденсатора достигнет первоначального максимального значения (поменяются знаки зарядов обкладок). Далее те же процессы начнут протекать в обратном направлении, и система к моменту времени 
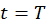придет в первоначальное состояние. После этого рассмотренный цикл разрядки и зарядки конденсатора будет повторяться. Причем в идеальном колебательном контуре такие колебания будут незатухающими. Периодически изменяться будут заряд конденсатора q, напряжение на конденсаторе U и сила тока I, текущего через катушку индуктивности.
В идеальном колебательном контуре напряжения на конденсаторе и катушке индуктивности в любой момент времени одинаковы
. (13.16)
Напряжение на конденсаторе найдем из определения емкости
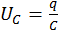. (13.17)
Напряжение на катушке равно э. д. с. самоиндукции, возникающей в ней, и из соответствующего закона равно
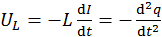, (13.18)
здесь учтено, что по определению сила тока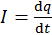 
. Подставляя (13.17) и (13.18) в (13.16) и вводя обозначение
, (13.19)
получим дифференциальное уравнение
. (13.20)
Очевидно, это уравнение математически тождественно полученному ранее уравнению (13.2) для механических колебаний, Значит его решением, также является гармоническая зависимость заряда конденсатора q от времени
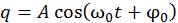, (13.21)
здесь все обозначения имеют те же обозначения и смысл, что и рассмотренные ранее, амплитуда колебаний представляет собой максимальный (начальный) заряд конденсатора qmax. Период колебаний:
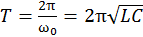. (13.22)
Напряжение на конденсаторе:
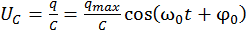. (13.23)
Сила тока через катушку индуктивности:
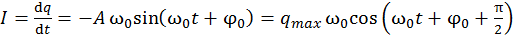. (13.24)
То есть колебания силы тока опережают по фазе колебания напряжения на . Энергии электрического и магнитного полей соответственно равны
(13.25)
и
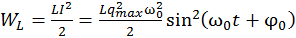. (13.26)
При этом полная (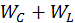 
) энергия контура в процессе колебаний не изменяется.
Примеры решения задач.
13.1. Материальная точка совершает гармонические колебания. Если при неизменной амплитуде уменьшить циклическую частоту колебаний в четыре раза, то как изменится максимальное значение возвращающей силы, действующей на точку?
Согласно (13.8) максимальное (амплитудное) значение ускорения точки 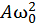и второй закон Ньютона для этого момента
.
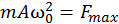Исходя из этого, при уменьшении ω0 в четыре раза,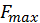 
уменьшится в два раза.
13.2. Уравнение движения материальной точки: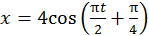 
см. Чему равен период колебаний этой точки?
Согласно () период колебаний связан с циклической частотой
.
Сравнивая заданное уравнение движения с (13.3), найдем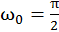 
. Подставив это значение, получим
с.
13.3. Пружина, к которой подвесили груз, растянулась на 41 мм. С какой частотой будет совершать колебания груз, если его вывести из положения равновесия?
Для груза, подвешенного на пружине (без колебаний), второй закон Ньютона дает равенство сил тяжести и упругости пружины:
.
Следовательно, отношение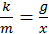 
. Частота колебаний груза с учетом (13.5) равна
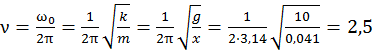Гц.
13.4. Математический маятник совершил 100 колебаний за 314 с. Чему равна длина маятника?
Чтобы найти период, надо время движения разделить на количество колебаний
.
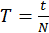Из соотношения (13.15) период колебаний математического маятника
.
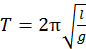Приравниваем эти выражения и находим длину маятника
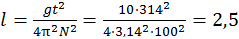м.
13.5. В электрическом колебательном контуре емкость конденсатора 2 мкФ, а максимальное напряжение на нем 5 В. Какова энергия магнитного поля катушки в момент времени, когда напряжение на конденсаторе равно 3 В?
Полная энергия колебательного контура в момент, когда напряжение на конденсаторе максимально, равна
.
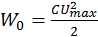Для таких колебаний выполняется закон сохранения энергии:
.
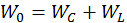Подставляя значения энергии конденсатора, выражаем энергию магнитного поля катушки
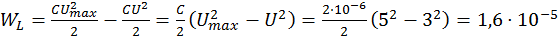Дж.
Дата добавления: 2021-02-10; просмотров: 55; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!