ЗАТУХАЮЩИЕ ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ
СОДЕРЖАНИЕ
| ВВЕДЕНИЕ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1 КОЛЕБАТЕЛЬНЫЕ ПРОЦЕССЫ В МЕХАНИКЕ . . . . . . . . . . . . . . . . 2 НЕЗАТУХАЮЩИЕ ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ . . . . . . . . . . . 2.1 Математический маятник . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2.2 Пружинный маятник . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2.3 Физический маятник . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2.4 Крутильный маятник . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3 ЗАТУХАЮЩИЕ ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ . . . . . . . . . . . . . 4 ЛАБОРАТОРНАЯ РАБОТА № 2. ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ ТЕЛ ПРИ ПОМОЩИ КРУТИЛЬНЫХ КОЛЕБАНИЙ . . . . . 4.1 Цель работы . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4.2 Описание установки . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4.3 Порядок выполнения работы . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4.4 Обработка результатов измерений . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4.5 Контрольные вопросы . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5 ЛАБОРАТОРНАЯ РАБОТА № 3. ИЗУЧЕНИЕ КОЛЕБАНИЙ МАЯТНИКА . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5.1 Цель работы . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5.2 Описание установки . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5.3 Порядок выполнения работы . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5.4 Обработка результатов измерений . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5.5 Контрольные вопросы . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ЛИТЕРАТУРА . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 4 4 5 7 8 9 10 11 14 14 14 15 15 17 18 18 18 19 19 21 22 |
|
|
|
ВВЕДЕНИЕ
Колебаниями называются процессы изменения состояния системы, характеризующиеся той или иной степенью повторяемости во времени. В зависимости от природы колебательного процесса различают колебания механические, электромагнитные и т.д. Однако, различные колебательные процессы в природе описываются однотипными уравнениями, что позволяет говорить о целесообразности единого подхода к изучению колебаний.
Данное учебное пособие посвящено экспериментальному изучению колебательных процессов в физике на примере свободных гармонических колебаний в механических системах, а так же определению характеристик колебательных систем.
КОЛЕБАТЕЛЬНЫЕ ПРОЦЕССЫ В МЕХАНИКЕ
Процессы в механике называются периодическими, если значения кинематических величин, характеризующих колебательную систему и изменяющихся при ее колебаниях, повторяются через равные промежутки времени.
Свободными (собственными) колебаниями называются колебания, которые происходят в отсутствие переменных внешних воздействий на колебательную систему и возникают вследствие отклонения системы от состояния устойчивого равновесия. При этом должна существовать некоторая возвращающая сила, которая стремится вернуть систему в равновесное положение. Такая возвращающая сила может представлять собой как конкретную физическую силу, так и равнодействующую нескольких сил.
|
|
|
Наиболее простыми в описании и часто встречающимися в природе колебаниями являются гармонические колебания, которые происходят под действием возвращающей квазиупругой силы, пропорциональной величине смещения тела из положения равновесия. Зависимость изменяющихся от времени характеристик системы при этом описывается гармонической функцией.
Наименьший промежуток времени T, удовлетворяющий условию периодичности кинематических величин называется периодом колебаний. За один период система совершает одно полное колебание. Частотой (или линейной частотой) ν колебаний называется число колебаний за единицу времени, частота обратно пропорциональна периоду колебаний: ν=1/T. Циклической (круговой частотой) ω называется величина, равная ω=2πν. Линейная частота измеряется в герцах, круговая частота — в радианах в секунду.
|
|
|
НЕЗАТУХАЮЩИЕ ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ
Рассмотрим собственные колебания, которые могут продолжаться бесконечно долго. Очевидно, что это возможно лишь в условиях отсутствия диссипативных сил.
Наиболее простыми в описании колебаниями являются гармонические колебания, которые происходят под действием возвращающей квазиупругой силы, которая пропорциональна величине смещения тела из положения равновесия. Зависимость изменяющихся от времени характеристик системы при этом описывается гармонической функцией (синус или косинус).
Рассмотрим материальную точку массой m, движущуюся вдоль оси O x, под действием квазиупругой силы F:
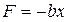, (1)
где b — некоторый коэффициент,
x — координата точки (предполагается, что точка имеет нулевую координату в положении равновесия).
Знак минус указывает на то, что направление силы противоположно направлению смещения точки из положения равновесия.
Тогда второй закон Ньютона будет записываться следующим образом (с учетом того, что ускорение является второй производной координаты по времени):
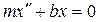. (2)
Полученное уравнение, связывающее вторую производную функции x(t) с ее значением называется дифференциальным уравнением. В общем случае решение дифференциальных уравнений является достаточно нетривиальной задачей, но для данного типа уравнений оно может быть записано в виде гармонической функции:
|
|
|
, (3)
где x0 — максимальное значение переменной величины x(t), оно называется амплитудой колебаний и имеет смысл максимального отклонения материальной точки от положения равновесия;
ω0 — круговая частота собственных колебаний;
φ0 — начальная фаза колебаний.
При этом аргумент гармонической функции называется фазой колебаний. Заметим, что в решении (3) может быть использована функция cos, однако, в этом случае значение начальной фазы φ0 будет другим.
При подстановке общего решения (3) в дифференциальное уравнение (2) мы получим обязательное условие решения:
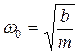. (4)
Из формулы (4) видно, что круговая частота собственных колебаний ω0определяется свойствами самой системы (в данном случае массой m и коэффициентом b). Оставшиеся два параметра колебательного процесса — амплитуда x0 и начальная фаза φ0— находятся из известных значений координаты и проекции на ось O x скорости материальной точки в начальный момент времени:
, 
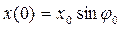. (5)
Зная зависимости координаты x(t) и проекции скорости V ( t ), можно получить выражения для потенциальной E P и кинетической E K энергии системы при незатухающих гармонических колебаниях:
, 
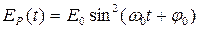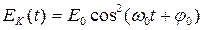,(6)
где E0 — полная механическая энергия системы.
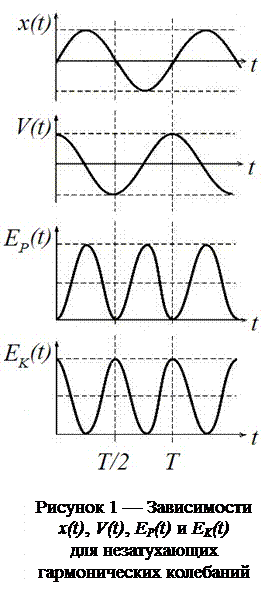На рисунке 1 представлены зависимости координаты x(t), скорости V ( t ), потенциальной EP ( t ) и кинетической EK ( t ) энергии тела для случая незатухающих гармонических колебаний. Скорость V ( t ) опережает по фазе смещение тела на π/2. Обе величины изменяются с периодом T.
Кинетическая и потенциальная энергии имеют вдвое большую циклическую частоту колебаний 2ω0 (и, следовательно, вдвое меньший период T /2), чем смещение и скорость тела. Это связано с тем, что зависимости EP ( t ) от смещения и EK ( t ) от скорости носят квадратичный характер и не зависят от знака проекции кинематической величины в разных полупериодах колебаний.
В следующих разделах мы рассмотрим ряд механических систем, в которых могут возникать свободные незатухающие гармонические колебания. Предполагается, что отклонения тел от положения равновесия являются малыми, это позволяет считать возвращающую силу прямо пропорциональной смещению.
Математический маятник
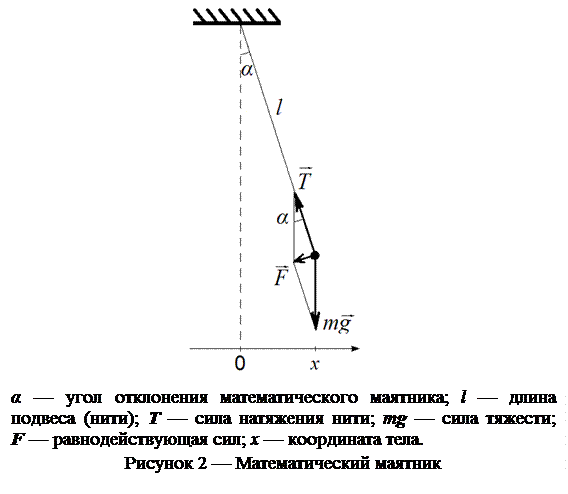
Математическим маятником является тело, подвешенное на нити много длиннее размеров самого тела (см. рисунок 2); в этом случае тело является материальной точкой.
При малых углах отклонения маятника α можно полагать, что sin α » tg α » α. В этом случае квазиупругая возвращающая сила и координата тела записываются как:
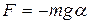, (7)
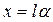, (8)
где l — длина нити.
Второй закон Ньютона для математического маятника:
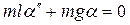, (9)
а его решение — функция α( t ) и частота собственных колебаний ω0:
, (10)
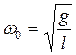. (11)
Мы видим, что частота собственных колебаний математического маятника ω0не зависит от массы материальной точки.
Пружинный маятник
Пружинный маятник изображен на рисунке 3. Предполагается, что тело массой m скользит по горизонтальной поверхности без трения. Согласно закону Гука, возвращающая сила равна:
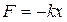, (12)
где k — жесткость пружины;
x — смещение тела из положения равновесия.
Второй закон Ньютона в проекции на ось O x будет иметь вид:
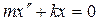(13)
Решение дифференциального уравнения (13) выражается формулами (14) и (15):
, (14)
. (15)
Заметим, что изменение положения пружинного маятника с горизонтального на вертикальное не изменит решение (14) и (15), поскольку сила тяжести не будет являться возвращающей силой. Действие силы тяжести сведется лишь к изменению положения равновесия тела на пружине.
В двух рассмотренных выше примерах мы полагали тело материальной точкой. Это привело к тому, что найденные частоты собственных колебаний (см. формулы (11) и (15)) не зависят от формы и размеров тел, распределения массы. В следующих разделах мы увидим, как влияет учет этих параметров на частоту собственных колебаний реальных твердых тел.
Физический маятник
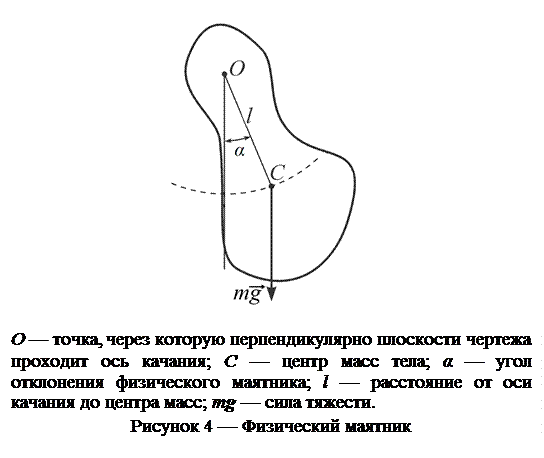
В отличие от математического, физический маятник имеет размеры тела, сравнимые с размерами системы. К примеру, у физического маятника на рисунке 4 расстояние l от оси вращения (точка O) до центра масс (точка С) меньше размера тела.
Поскольку в данном случае мы не можем считать тело материальной точкой, то мы должны его рассматривать как абсолютно твердое тело, а колебания — как вращение вокруг оси, проходящей через точку O. Уравнение движения мы получим из рассмотрения основного закона динамики вращательного движения:
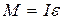, (16)
где: M — момент силы, действующей на колеблющийся маятник; I — момент инерции тела;
ε — угловое ускорение тела.
При небольших углах α отклонения маятника:
. (17)
Тогда основной закон динамики вращательного движения для переменной α записывается как:
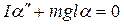, (18)
а его решение будет выражаться формулами (19) и (20):
, (19)
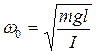. (20)
Сравнивая частоты собственных колебаний математического (11) и физического (20) маятников мы видим, что при усложнении колебательной системы частота собственных колебаний начинает зависеть от большего числа параметров. В то же время формула (20) переходит в формулу (11) при увеличении длины подвеса до размеров существенно больше размеров тела, когда момент инерции тела I = ml 2 .
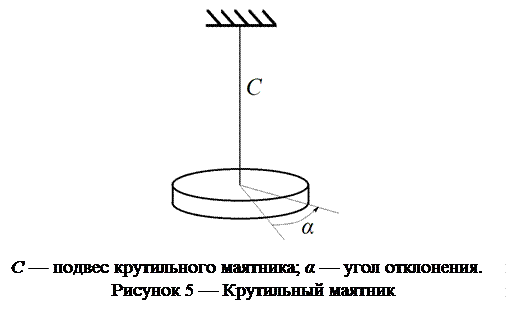
Крутильный маятник
Крутильный маятник представляет собой тело, подвешенное на упругой нити (чаще всего используется металлическая проволока) и совершающее крутильные колебания в плоскости перпендикулярной подвесу (см. рисунок 5). В отличие от предыдущего случая, здесь ось вращения проходит через центр масс твердого тела.
Закручивание проволоки ведет к возникновению момента упругих сил, который при малых углах поворота α можно считать равным:
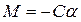, (21)
где С — коэффициент, зависящий от упругих свойств нити.
Основной закон динамики вращательного движения для переменной α будет записываться как:
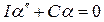, (22)
а его решением будет:
, (23)
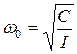. (24)
ЗАТУХАЮЩИЕ ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ
В рассмотренных ранее примерах колебательного движения не учитывались силы сопротивления среды, приводящие к затуханию свободных колебаний в механической системе.
Мы будем рассматривать не сухое трение, а вязкое сопротивление среды. Запишем силу сопротивления среды FC как величину пропорциональную скорости движения тела в данной среде:
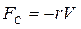, (25)
где r — коэффициент сопротивления среды. Данная зависимость справедлива при движении с малыми скоростями в вязкой среде.
Пусть выражение для квазиупругой возвращающей силы задается формулой (1), тогда второй закон Ньютона будет записываться следующим образом (с учетом того, что скорость тела является первой производной координаты по времени, а ускорение — второй производной):
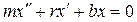. (26)
Поделим это выражение на массу и получим:
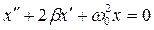, (27)
где: β = r/2m — коэффициент затухания;
ω0 — уже знакомая нам частота собственных незатухающих колебаний, см. формулу (4):
.
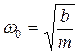Решение дифференциального уравнения (27) выражается в виде произведения гармонической функции и убывающей экспоненты:
, (28)
где A0 — начальная амплитуда;
ω — циклическая частота затухающих колебаний.
Частота затухающих колебаний ω не совпадает с частотой собственных колебаний ω0. Значение ω можно получить после подстановки решения (28) в уравнение (27):
. (29)
Обратите внимание, что частота затухающих колебаний всегда должна быть меньше частоты собственных незатухающих колебаний ω0 (а период, соответственно, больше). Упрощенно это можно объяснить очевидным замедлением движения тела в вязкой среде.
Иногда решение (28) представляют в виде гармонических колебаний с экспоненциально уменьшающейся амплитудой:
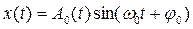, (30)
где A ( t ) — зависящая от времени амплитуда колебаний:
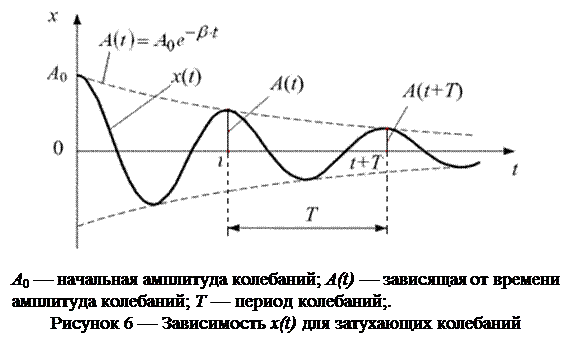
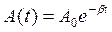. (31)
График зависимости координаты тела от времени x(t) для затухающих колебаний приведен на рисунке 6. В данном случае процесс движения является периодическим с периодом Т=2π/ω.
При увеличении коэффициента сопротивления среды r (а значит и коэффициента затухания β) период затухающих колебаний
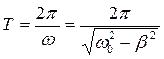(32)
возрастает. При приближении β к ω0 период Т должен стремиться к бесконечности. Если же β > ω0, то колебания в системе становятся невозможны. В таком случае выведенная из состояния равновесия и предоставленная самой себе система возвращается в положение равновесия не совершая колебаний. Такое движение называется апериодическим. На рисунке 7 представлены примеры зависимостей x(t) для апериодических процессов.
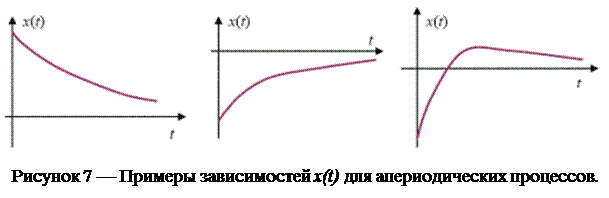
Как уже говорилось, процесс затухания свободных колебаний характеризуется коэффициентом затухания β. Обратная к коэффициенту затухания величина τ=1/β называется временем релаксации и имеет смысл промежутка времени, в течение которого происходит уменьшение амплитуды колебаний в е раз.
Если A ( t ) и A ( t + T ) — амплитуды двух последовательных колебаний, соответствующих моментам времени, отличающихся на период (см. рисунок 6), то отношение
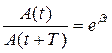(33)
называется декрементом затухания, а его натуральный логарифм:
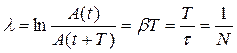(34)
называется логарифмическим декрементом затухания. Здесь N — число колебаний, совершаемое за время уменьшения амплитуды колебаний в е раз.
4 ЛАБОРАТОРНАЯ РАБОТА № 2
«ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ ТЕЛ ПРИ ПОМОЩИ КРУТИЛЬНЫХ КОЛЕБАНИЙ»
Цель работы
Цель данной работы — экспериментальное определение момента инерции тел при помощи крутильного маятника и сравнение полученных значений с расчетными.
Описание установки
Установка показана на рисунке 8 и представляет собой крутильный маятник с возможностью крепления тел разной формы. К цилиндрической головке Г, расположенной на штативе Ш крепится конец металлической проволоки Н. Другойконец проволоки зафиксирован в цилиндре Ц, в котором есть винтовые крепления для тела Д в различных положениях и стержня С.
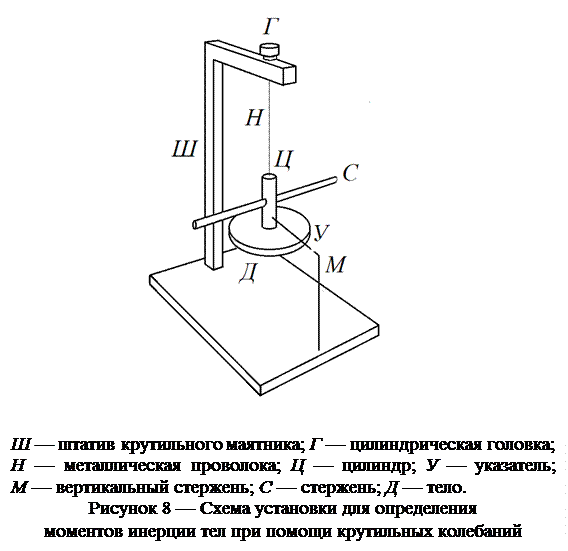
Указатель У, перемещающийся в процессе колебаний относительно неподвижного вертикального стержня М, позволяет визуально следить за крутильными колебаниями маятника.
В данной лабораторной работе экспериментально определяются моменты инерции тела Д для различных положений оси вращения.Тело Д имеет вид плоской фигуры и может крепиться к цилиндру Ц двумя различными способами. Стержень С с известным значением момента инерции используется в качестве эталонного тела.
Порядок выполнения работы
Сначала на весах взвешивают стержень С и измеряют линейкой его длину. Измеряют размеры и массу тела Д.
Далее, стержень вставляют в отверстие цилиндра Ц так, чтобы ось, вокруг которой колеблется система, проходила через середину стержня. Стержень закрепляют винтом и возбуждают крутильные колебания путем поворота цилиндрической головки Г на некоторый угол и возврата ее в исходное положение. Для определения периода крутильных колебаний стержня T0 замеряют время, за которое совершается 10–20 полных колебаний стержня. Эксперимент повторяют три раза.
Далее, возбуждают крутильные колебания системы, состоящей из стержня С и закрепленного на цилиндре Ц тела Д. Тело крепится таким образом, чтобы ось вращения была перпендикулярна плоскости тела (такое положение тела относительно оси вращения называется полярным, см рисунок 8). Определяют период крутильных колебаний системы T, трижды замерив время, за которое совершается 10–20 полных колебаний.
Затем меняют положение тела Д на цилиндре, таким образом, чтобы ось вращения лежала в плоскости тела (такое положение тела относительно оси вращения называется экваториальным). И, аналогично предыдущему случаю, определяют период крутильных колебаний системы.
Дата добавления: 2021-02-10; просмотров: 59; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!