Общая схема исследования функции
И построение графика функции.
1. Найти область определения функции.
2. Найти точки пересечения графика с осями координат.
3. Найти интервалы знакопостоянства функции.
4. Установить чётность и периодичность функции.
5. Найти асимптоты графика функции.
6. Найти интервалы монотонности и экстремумы функции.
7. Найти интервалы выпуклости, вогнутости и точки перегиба графика функции.
8. Построить график функции.
Наибольшее и наименьшее значения функции на отрезке.
Пусть функция 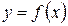 непрерывна на отрезке
непрерывна на отрезке 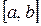 . Тогда на этом отрезке она достигает своих наибольшего и наименьшего значений. Эти значения функция может принять либо во внутренней точке
. Тогда на этом отрезке она достигает своих наибольшего и наименьшего значений. Эти значения функция может принять либо во внутренней точке 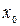 отрезка
отрезка 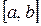 , либо на границе отрезка, т.е. при
, либо на границе отрезка, т.е. при 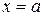 или
или 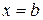 . Если
. Если 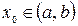 , то точку
, то точку 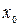 следует искать среди критических точек данной функции.
следует искать среди критических точек данной функции.
Получаем следующее правило нахождения наибольшего и наименьшего значений функции на 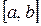 :
:
1. найти критические точки функции на интервале 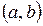 ;
;
2. вычислить значения функции в найденных критических точках;
3. вычислить значения функции на концах отрезка, т.е. в точках 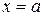 и
и 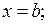
4. среди всех вычисленных значений функции выбрать наибольшее и наименьшее.
Индивидуальные задания для контрольной работы
Задача №1. Вычислить предел.
1.1. а) 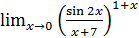 ; б)
; б) 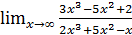 ;
;
в) 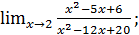 г)
г) 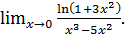
1.2 а) 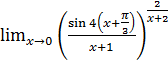 ; б)
; б) 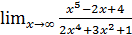 ;
;
в) 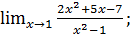 г)
г) 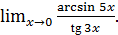
1.3 а) 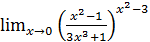 ; б)
; б) 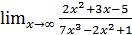 ;
;
|
|
|
в) 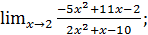 г)
г) 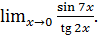
1.4 а) 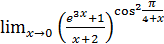 ; б)
; б) 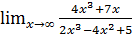 ;
;
в) 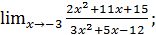 г)
г) 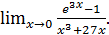
1.5 а) 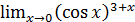 ; б)
; б) 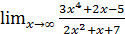 ;
;
в) 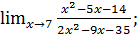 г)
г) 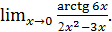
1.6 а) 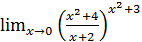 ; б)
; б) 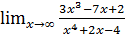 ;
;
в) 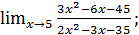 г)
г) 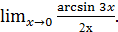
1.7 а) 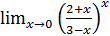 ; б)
; б) 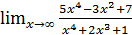 ;
;
в) 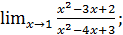 г)
г) 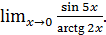
1.8 а) 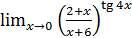 ; б)
; б) 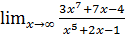 ;
;
в) 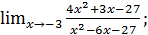 г)
г) 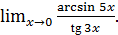
1.9 а) 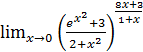 ; б)
; б) 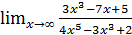 ;
;
в) 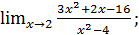 г)
г) 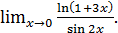
1.10 а) 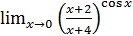 ; б)
; б) 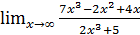 ;
;
в) 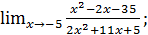 г)
г) 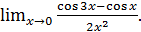
1.11 а) 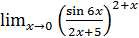 ; б)
; б) 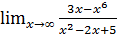 ;
;
в) 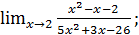 г)
г) 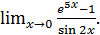
1.12 а) 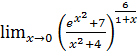 ; б)
; б) 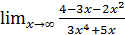 ;
;
в) 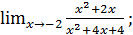 г)
г) 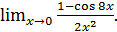
1.13 а) 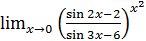 ; б)
; б) 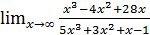 ;
;
в) 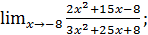 г)
г) 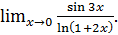
1.14 а) 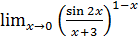 ; б)
; б) 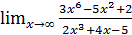 ;
;
в) 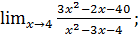 г)
г) 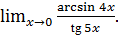
1.15 а) 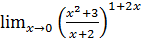 ; б)
; б) 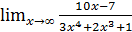 ;
;
в) 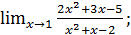 г)
г) 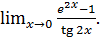
1.16 а) 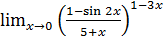 ; б)
; б) 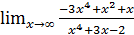 ;
;
в) 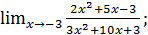 г)
г) 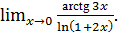
1.17 а) 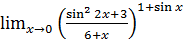 ; б)
; б) 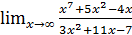 ;
;
в) 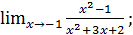 г)
г) 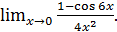
1.18 а) 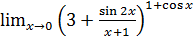 ; б)
; б) 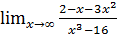 ;
;
в) 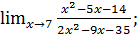 г)
г) 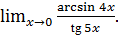
1.19 а) 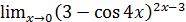 ; б)
; б) 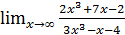 ;
;
в) 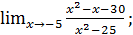 г)
г) 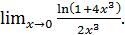
1.20 а) 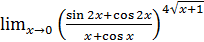 ; б)
; б) 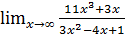 ;
;
в) 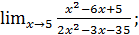 г)
г) 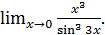
1.21 а) 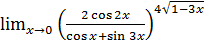 ; б)
; б) 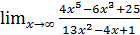 ;
;
в) 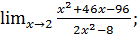 г)
г) 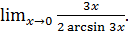
1.22 а) 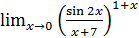 ; б)
; б) 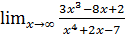 ;
;
в) 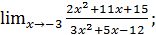 г)
г) 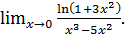
1.23 а) 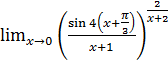 ; б)
; б) 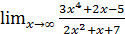 ;
;
в) 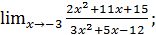 г)
г) 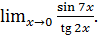
1.24 а) 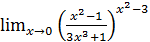 ; б)
; б) 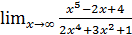 ;
;
|
|
|
в) 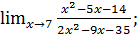 г)
г) 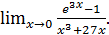
1.25 а) 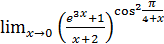 ; б)
; б) 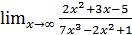 ;
;
в) 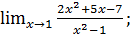 г)
г) 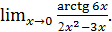
1.26 а) 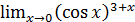 ; б)
; б) 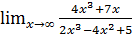 ;
;
в) 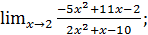 г)
г) 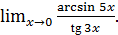
1.27 а) 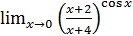 ; б)
; б) 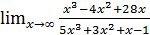 ;
;
в) 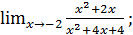 г)
г) 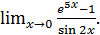
1.28 а) 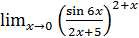 ; б)
; б) 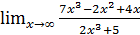 ;
;
в) 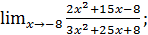 г)
г) 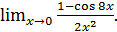
1.29 а) 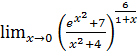 ; б)
; б) 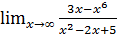 ;
;
в) 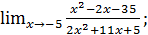 г)
г) 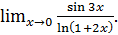
1.30 а) 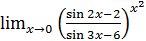 ; б)
; б) 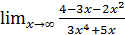 ;
;
в) 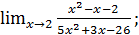 г)
г) 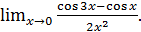
Задача №2. Найти производную функции 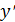 .
.
2.1 а) 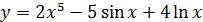 ; б)
; б) 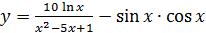 ;
;
в) 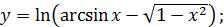 г)
г) 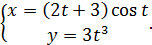
2.2 а) 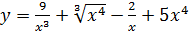 ; б)
; б) 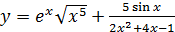 ;
;
в) 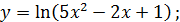 г)
г) 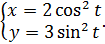
2.3 а) 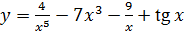 ; б)
; б) 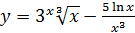 ;
;
в) 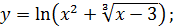 г)
г) 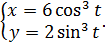
2.4 а) 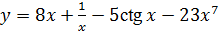 ; б)
; б) 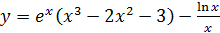 ;
;
в)  г)
г) 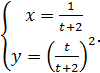
2.5 а) 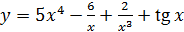 ; б)
; б) 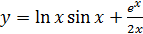 ;
;
в) 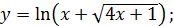 г)
г) 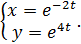
2.6 а) 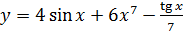 ; б)
; б) 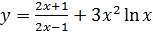 ;
;
в) 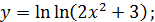 г)
г) 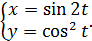
2.7 а) 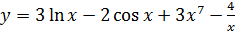 ; б)
; б) 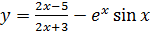 ;
;
в) 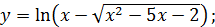 г)
г) 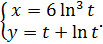
2.8 а) 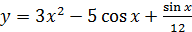 ; б)
; б) 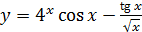 ;
;
в) 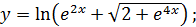 г)
г) 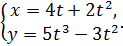
2.9 а) 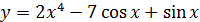 ; б)
; б) 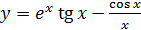 ;
;
в) 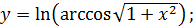 г)
г) 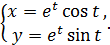
2.10 а) 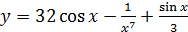 ; б)
; б) 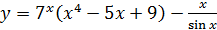 ;
;
в) 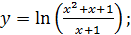 г)
г) 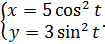
2.11 а) 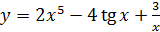 ; б)
; б) 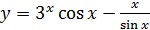 ;
;
в) 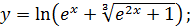 г)
г) 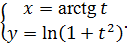
2.12 а) 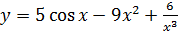 ; б)
; б) 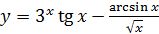 ;
;
в) 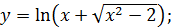 г)
г) 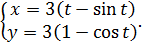
2.13 а) 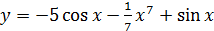 ; б)
; б) 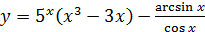 ;
;
в) 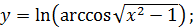 г)
г) 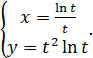
2.14 а) 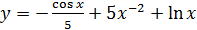 ; б)
; б) 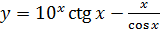 ;
;
в) 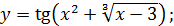 г)
г) 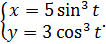
2.15 а) 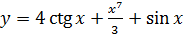 ; б)
; б) 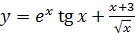 ;
;
в) 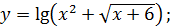 г)
г) 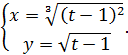
2.16 а) 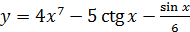 ; б)
; б) 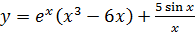 ;
;
в) 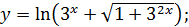 г)
г) 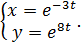
2.17 а) 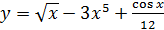 ; б)
; б) 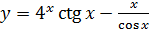 ;
;
в) 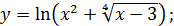 г)
г) 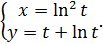
2.18 а) 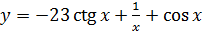 ; б)
; б) 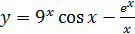 ;
;
в) 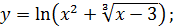 г)
г) 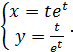
2.19 а) 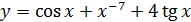 ; б)
; б) 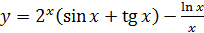 ;
;
в) 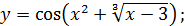 г)
г) 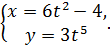
|
|
|
2.20 а) 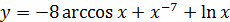 ; б)
; б) 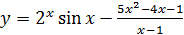 ;
;
в) 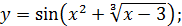 г)
г) 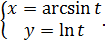
2.21 а) 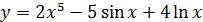 ; б)
; б) 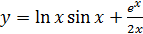 ;
;
в)  г)
г) 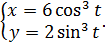
2.22 а) 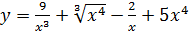 ; б)
; б) 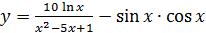 ;
;
в) 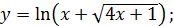 г) )
г) ) 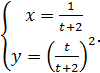
2.23 а) 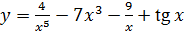 ; б)
; б) 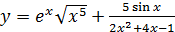 ;
;
в) 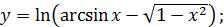 г)
г) 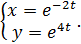
2.24 а) 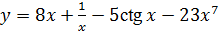 ; б)
; б) 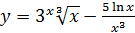 ;
;
в) 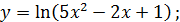 г)
г) 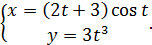
2.25 а) 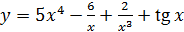 ; б)
; б) 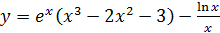 ;
;
в) 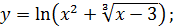 г)
г) 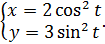
2.26 а) 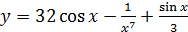 ; б)
; б) 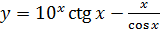 ;
;
в) 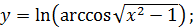 г)
г) 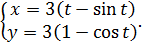
2.27 а) 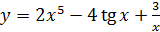 ; б)
; б) 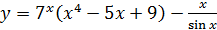 ;
;
в) 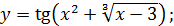 г)
г) 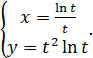
2.28 а) 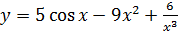 ; б)
; б) 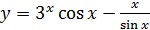 ;
;
в) 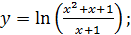 г)
г) 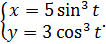
2.29 а) 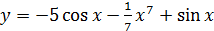 ; б)
; б) 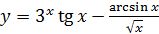 ;
;
в) 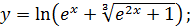 г)
г) 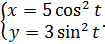
2.30 а) 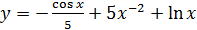 ; б)
; б) 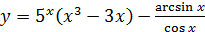 ;
;
в) 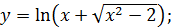 г)
г) 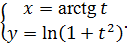
Задача №3. Найти дифференциал функции 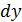 .
.
3.1 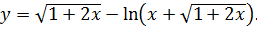
3.2 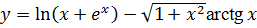 .
.
3.3 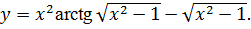
3.4 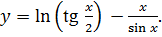
3.5 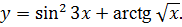
3.6 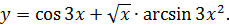
3.7 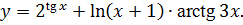
3.8 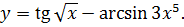
3.9 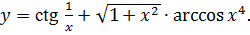
3.10 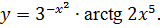
3.11 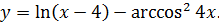
3.12 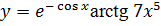
3.13 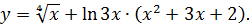
3.14 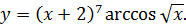
3.15 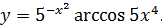
3.16 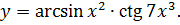
3.17 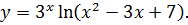
3.18 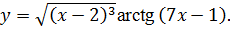
3.19 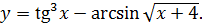
3.20 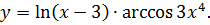
3.21 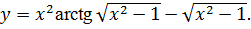
3.22 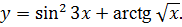
3.23 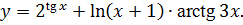
3.24 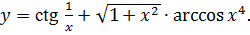
3.25 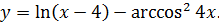
3.26 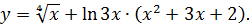
3.27 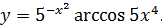
3.28 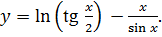
3.29 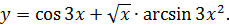
3.30 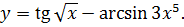
Задача №4. Вычислить приближенно с помощью дифференциала.
4.1 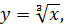
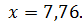
4.2 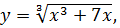
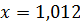 .
.
4.3 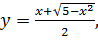
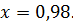
4.4  .
.
4.5 
4.6 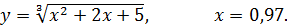
4.7 
4.8 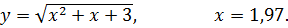
4.9 
4.10 
4.11 
4.12 
4.13 
4.14 
4.15 
4.16 
4.17 
4.18 
4.19 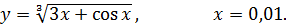
4.20 
4.21 
4.22 
4.23 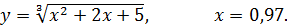
4.24 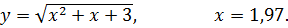
4.25 
4.26 
4.27 
4.28 
4.29 
4.30 
Задача №5. Составить уравнения касательной и нормали к данной кривой в точке с абсциссой
5.1 
5.2 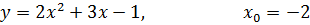 .
.
5.3 
5.4 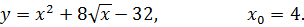
5.5 
5.6 
5.7 
5.8 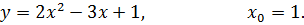
5.9 
5.10 
5.11 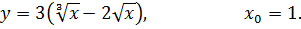
5.12 
5.13 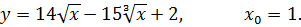
5.14 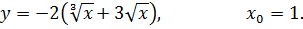
5.15 
5.16 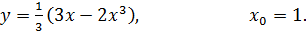
5.17 
5.18 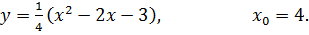
5.19 
5.20 
5.21 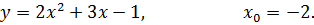
5.22 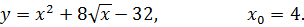
5.23 
5.24 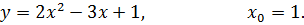
5.25 
5.26 
5.27 
5.28 
5.29 
5.30 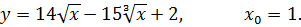
|
|
|
Задача №6. Найти производную второго порядка 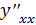 :
:
6.1 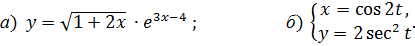
6.2 
6.3 
6.4 
6.5 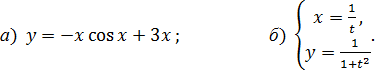
6.6 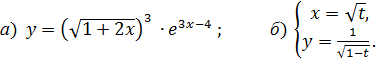
6.7 
6.8 
6.9 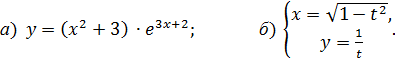
6.10 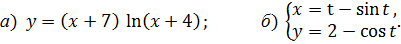
6.11 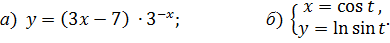
6.12 
6.13 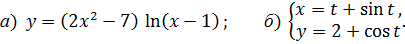
6.14 
6.15 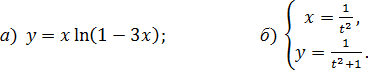
6.16 
6.17 
6.18 
6.19 
6.20 
6.21 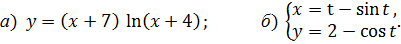
6.22 
6.23 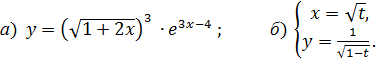
6.24 
6.25 
6.26 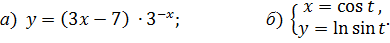
6.27 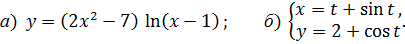
6.28 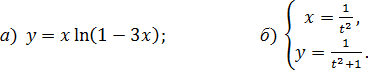
6.29 
6.30 
Задача №7. а) найти наибольшее и наименьшее значения функции на заданном промежутке.
б) провести полное исследование функции и построить её график.
7.1 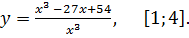
7.2 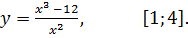
7.3 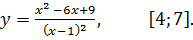
7.4 
7.5 
7.6 
7.7 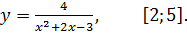
7.8 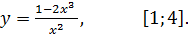
7.9 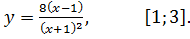
7.10 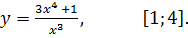
7.11 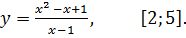
7.12 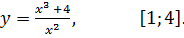
7.13 
7.14 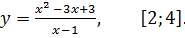
7.15 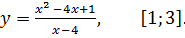
7.16 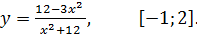
7.17 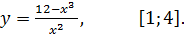
7.18 
7.19 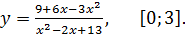
7.20 
7.21 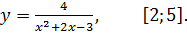
7.22 
7.23 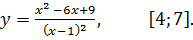
7.24 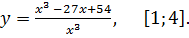
7.25 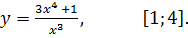
7.26 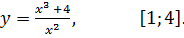
7.27 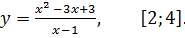
7.28 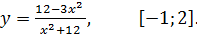
7.29 
7.30 
Решение типового варианта.
Задача № 1. Вычислить предел функции
а) 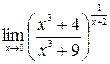 .
.
Решение. Воспользуемся свойством 6. Так как
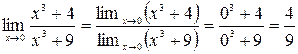 и
и 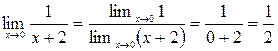 ,
,
то 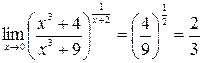 .
.
б) 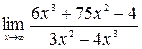 .
.
Решение. Имеем неопределенность 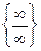 . Для ее раскрытия разделим числитель и знаменатель на
. Для ее раскрытия разделим числитель и знаменатель на 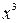 :
:
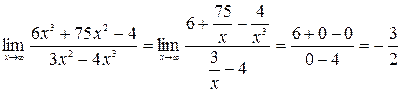 .
.
в) 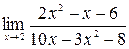 .
.
Решение. Здесь имеем дело с неопределенностью 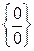 . Разложим числитель и знаменатель на множители:
. Разложим числитель и знаменатель на множители:
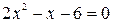 ,
, 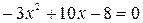 ,
,
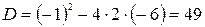 ,
, 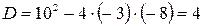 ,
,
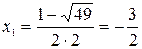 ,
, 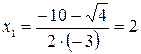 ,
,
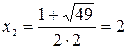 .
. 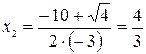 .
.
Тогда 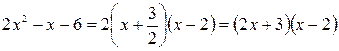 ,
,
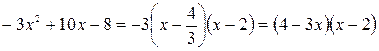 .
.
Получим
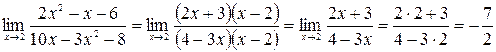 .
.
г) 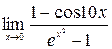 .
.
Решение. Снова имеем дело с неопределенностью 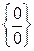 . Воспользуемся таблицей эквивалентности б.м.ф. при
. Воспользуемся таблицей эквивалентности б.м.ф. при 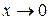 :
:
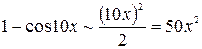 ,
, 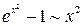 .
.
Тогда
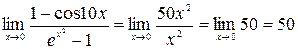 .
.
Задача № 2. Найти производную данной функции
а) 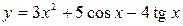 .
.
Решение. Согласно свойствам 2 и 1, а также таблице производной, получим:
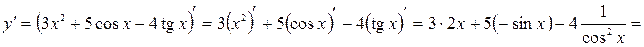
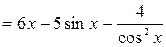 .
.
б) 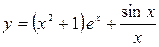 .
.
Решение. Воспользуемся свойствами 2, 3 и 4:
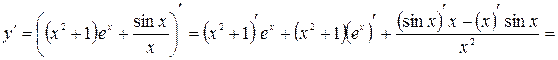
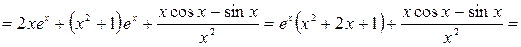
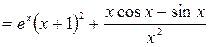 .
.
в) 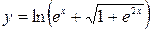 .
.
Решение. Здесь дана сложная функция. Поэтому, согласно формуле (2.1) получим:
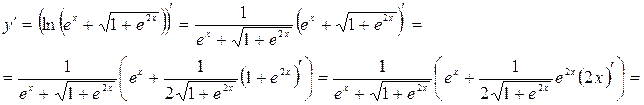
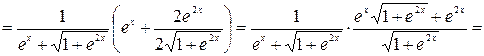
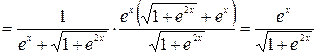 .
.
г) 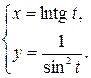
Решение. Функция задана параметрически. Вычислим сначала производные 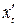 и
и 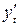 :
:
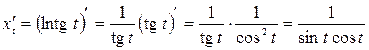 ,
,
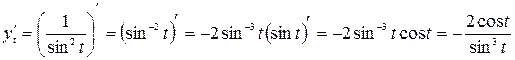 .
.
По формуле (2.2)получим:
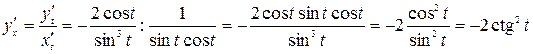 .
.
Задача № 3. Найти дифференциал 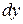 заданной функции
заданной функции
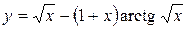 .
.
Решение. Согласно формуле (2.6) имеем: 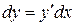 . Поэтому вычислим сначала производную данной функции
. Поэтому вычислим сначала производную данной функции
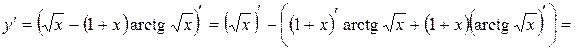
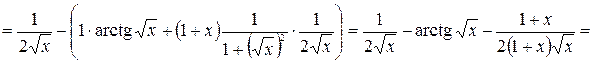
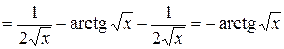 .
.
Получим: 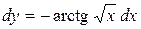 .
.
Задача № 4. Вычислить приближенно с помощью дифференциала значение функции 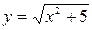 в точке
в точке 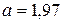 .
.
Решение. По формуле (2.9) имеем: 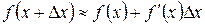 .
.
Примем 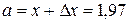 , где
, где 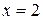 , а
, а 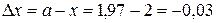 .
.
Найдем производную:
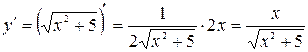 .
.
Тогда
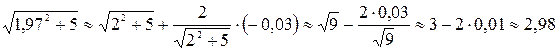 .
.
Задача № 5. Написать уравнения касательной и нормали к кривой 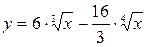 в точке с абсциссой
в точке с абсциссой 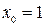 .
.
Решение. Вычислим значение функции в точке 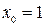 :
: 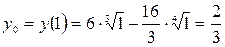 .
.
Найдем производную функции и вычислим ее значение в точке 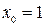 :
:
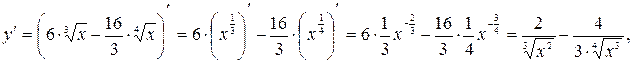
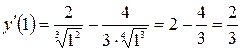 .
.
По формуле (2.7) уравнение касательной принимает вид:
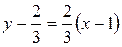 или
или 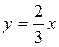 .
.
Согласно формуле (2.8) получим уравнение нормали:
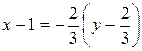 или
или 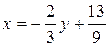 , что равносильно
, что равносильно 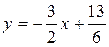 .
.
Задача № 6. Найти производную второго порядка.
а) 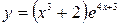 .
.
Решение. Вычислим сначала 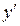 :
:
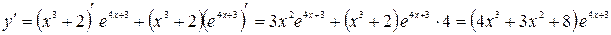 .
.
А затем по формуле (2.3) получим:
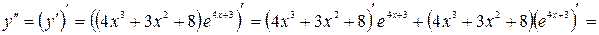
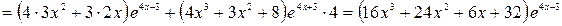 .
.
б) 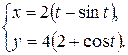
Решение. Вычислим 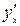 :
:
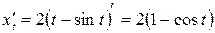 ,
, 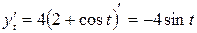 .
.
Тогда по формуле (2.2): 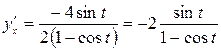 .
.
Найдем производную 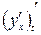 :
:
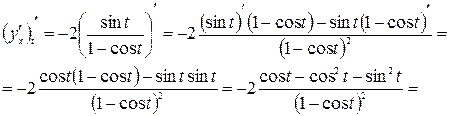
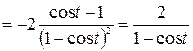 .
.
По формуле (2.5) имеем:
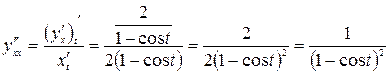 .
.
Задача № 7. а) Найти наибольшее и наименьшее значения функции 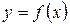 на отрезке
на отрезке 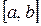 .
.
б) Провести полное исследование данной функции и построить ее график.
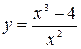 ,
, 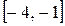 .
.
Решение. а) Воспользуемся правилом, рассмотренным в п. 3.6. Найдем критические точки функции, принадлежащие отрезку 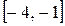 :
:
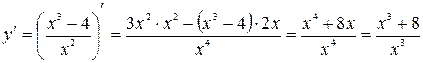 ,
,
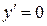 при
при 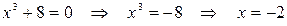 ,
,
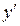 – не существует при
– не существует при 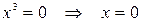 .
.
Заметим, что 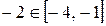 , а
, а 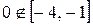 .
.
Вычислим значения функции во внутренней критической точке и на концах отрезка:
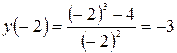 ,
, 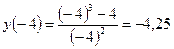 ,
, 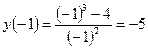 .
.
Из найденных значений выберем наименьшее и наибольшее:
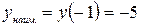 ,
, 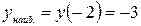 .
.
б) Используем общую схему исследования функции, рассмотренную в п. 3.5.
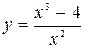
1. Область определения функции 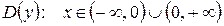 .
.
2. Точки пересечения графика функции с осями координат:
С Ох : 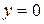 при
при 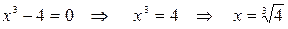 ,
,
С Оу : если 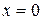 , то
, то 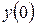 – не существует.
– не существует.
Следовательно, есть только одна точка пересечения с осями – 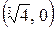 .
.
3. Определим промежутки знакопостоянства функции.
Точки 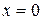 и
и 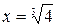 разбивают область определения на три интервала знакопостоянства функции:
разбивают область определения на три интервала знакопостоянства функции: 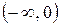 ,
, 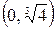 и
и 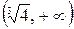 . Определим знак функции на каждом интервале:
. Определим знак функции на каждом интервале:
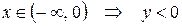 ,
, 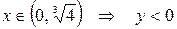 ,
, 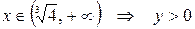 .
.
4. Установим чётность функции.
 .
.
Очевидно, что 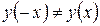 и
и 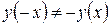 , следовательно, данная функция не является чётной и не является нечётной, т.е. является функцией общего вида.
, следовательно, данная функция не является чётной и не является нечётной, т.е. является функцией общего вида.
5. Найдём асимптоты.
а) Вертикальные асимптоты: 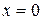 .
.
б) Наклонные асимптоты:
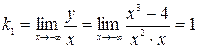 ,
, 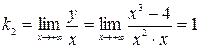 .
.
Так как 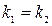 , то и
, то и 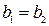 .
.
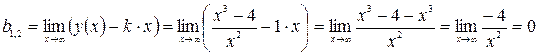 .
.
Получили 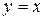 – наклонная асимптота.
– наклонная асимптота.
6. Интервалы монотонности. Экстремумы.
В пункте (а) мы нашли критические точки функции: 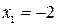 и
и 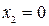 . Эти точки разбивают область определения на три промежутка монотонности:
. Эти точки разбивают область определения на три промежутка монотонности: 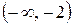 ,
, 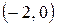 и
и 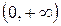 . Определим знак производной функции
. Определим знак производной функции 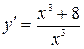 на каждом интервале.
на каждом интервале.
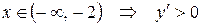 ,
, 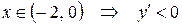 ,
, 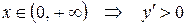 .
.
Следовательно, при 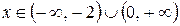 – функция возрастает, а при
– функция возрастает, а при 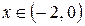 – функция убывает.
– функция убывает.
При переходе (слева на право) через критические точки производная меняет свой знак, но 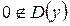 , поэтому функция имеет только одну точку экстремума:
, поэтому функция имеет только одну точку экстремума:
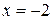 – точка max и
– точка max и 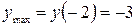 .
.
Таким образом: 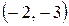 – максимальная точка функции.
– максимальная точка функции.
7. Выпуклость, вогнутость. Точки перегиба.
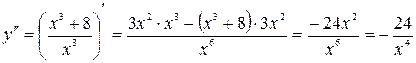 ,
,
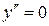 : точек нет, т.к.
: точек нет, т.к. 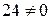 ,
,
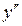 – не существует при
– не существует при 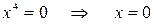 .
.
Определим знаки второй производной на интервалах 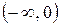 и
и 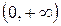 . На обоих интервалах
. На обоих интервалах 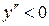 , следовательно, на всей области определения график функции вогнут, и точек перегиба нет.
, следовательно, на всей области определения график функции вогнут, и точек перегиба нет.
8. Построим график функции.
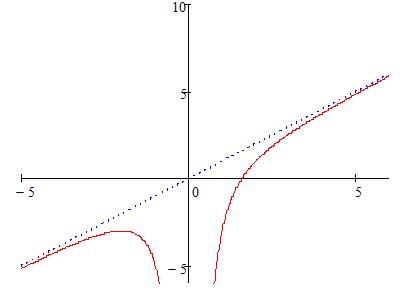
Рис. 1.
Литература
а) Список использованной литературы
1. Сборник индивидуальных заданий по высшей математике. Ч. 1. Под ред. Рябушко А.П.– Минск: Вышэйшая школа, 1990.
2. Кузнецов Л.А. Сборник заданий по высшей математике. ТР. М.: Высшая школа, 1983 г., 2005 г.
3. Данко П.Е. и др. Высшая математика в упражнениях и задачах. Ч. 1. М.: Высшая школа, 1980 г.
4. Пискунов Н.С. Дифференциальное и интегральное исчисление.
Т. 1. М.: Наука, 1978 г.
б) Список рекомендуемой литературы
1. Пискунов Н.С. Дифференциальное и интегральное исчисление.
Т. 1. М.: Наука, 1978 г.
2. Бугров Я.С., Никольский С.М. Дифференциальное и интегральное исчисление. М.: Наука, 1980 г.
3. Данко П.Е. и др. Высшая математика в упражнениях и задачах. Ч. 1. М.: Высшая школа, 1980 г.
4. Письменый Д.Т. Конспект лекций по высшей математике: полный курс/Д.Т. Письменный. – 4-е изд. – М: Айрис-пресс, 2006. 608 с.
5. Зимина О.В., Кириллов А.И., Сальникова Т.А. Высшая математика. ( Серия "решебник") 2-е изд., испр. – М.: Физико-математическая литература, 2001. – 368 с. (Решебник.) URL: http://www.alleng.ru/d/math/math164.htm
6. Запорожец Г.И. Руководство к решению задач по математическому анализу. 4-е изд., М.: Высшая школа, 1966. - 464с. URL: http://www.alleng.ru/d/math/math24.htm
7. Смолянский М.Л. Таблицы неопределенных интегралов. 2-е изд., испр. - М.: Гос. изд. физ-мат. лит., 1963. - 112с. URL: http://www.alleng.ru/d/math/math208.htm
Оглавление
1. Предел функции……………………………………………………....3
2. Дифференциальное исчисление функции одного переменного… .6
3. Исследование функции…………………………………………...…10
4. Индивидуальные задания для контрольной работы………………14
5. Решение типового варианта…………………………………..…….31
6. Литература………………………………………………………...…40
Дата добавления: 2021-01-21; просмотров: 111; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
