Дифференциальное исчисление функции одного переменного.
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
«Ковровская государственная технологическая академия имени В.А. Дегтярева»
ПРЕДЕЛЫ. ПРОИЗВОДНЫЕ.
Контрольная работа по математике для заочного отделения.
Миронова Е.А.
Юлина Н.А.
г. Ковров 2013 г.
Методические указания предназначены в качестве пособия для студентов заочного отделения технических специальностей. Содержат в себе сжатый теоретический материал и индивидуальные задания к первой контрольной работе по математике.
Предел функции.
Пусть функция 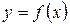 определена в некоторой окрестности точки
определена в некоторой окрестности точки 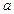 , кроме, быть может, самой этой точки.
, кроме, быть может, самой этой точки.
Число 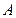 называется пределом функции
называется пределом функции 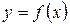 при
при 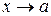 , если для любого положительного числа
, если для любого положительного числа 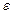 найдется такое положительное число
найдется такое положительное число 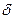 , что для всех
, что для всех 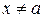 , удовлетворяющих неравенству
, удовлетворяющих неравенству 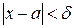 , выполняется неравенство
, выполняется неравенство 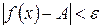 .
.
Записывают: 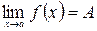 .
.
Перечислим свойства пределов функции, которые облегчают решение задачи отыскания пределов:
1. 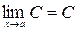 , где
, где 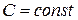 .
.
2. 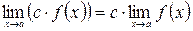 .
.
3. 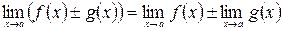 .
.
4. 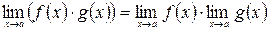 .
.
5. 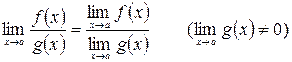 .
.
6. если 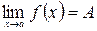 и
и  , то
, то 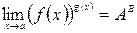 .
.
При этом предполагается, что все пределы существуют. Точка 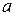 может быть как действительным числом, так и
может быть как действительным числом, так и 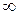 .
.
Если при отыскании пределов функций возникает ситуация, когда невозможно напрямую применить вышеперечисленные свойства, то имеет место неопределенность и возникает задача раскрытия неопределенности.
|
|
|
Наиболее часто встречаются неопределенности вида: 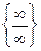 ,
, 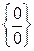 ,
, 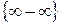 ,
, 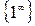 .
.
Рассмотрим некоторые методы раскрытия этих неопределенностей.
1.1 Неопределенность 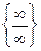 . Отношение многочленов.
. Отношение многочленов.
Если Pn(x) и Q m(x) – многочлены степени n и m, и 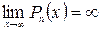 и
и 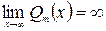 , то при вычислении
, то при вычислении 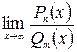 имеем неопределённость
имеем неопределённость 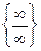 . Для её раскрытия делим числитель и знаменатель на х в наибольшей степени. При этом стоит помнить, что
. Для её раскрытия делим числитель и знаменатель на х в наибольшей степени. При этом стоит помнить, что  и
и 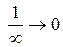 .
.
1.2 Неопределенность 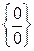 .
.
а) Отношение многочленов.
Если 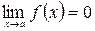 и
и 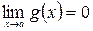 , то при вычислении
, то при вычислении 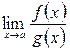 имеем неопределённость вида
имеем неопределённость вида 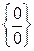 . Для её раскрытия необходимо числитель и знаменатель разложить на простейшие множители, т.е. представить функции
. Для её раскрытия необходимо числитель и знаменатель разложить на простейшие множители, т.е. представить функции  и
и 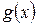 в виде:
в виде: 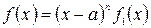 и
и 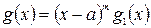 , где
, где 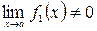 и
и 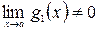 .
.
Тогда
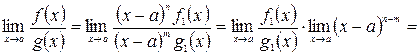
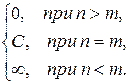
При этом 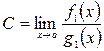 .
.
б) Первый замечательный предел.
Для отыскания пределов функций вида 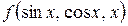 (здесь
(здесь 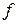 – некоторая функция) может быть использован так называемый первый замечательный предел
– некоторая функция) может быть использован так называемый первый замечательный предел
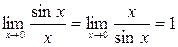 . (1.1)
. (1.1)
в) Общий случай.
Если 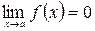 , то
, то  называется бесконечно малой функцией (б.м.ф.) в окрестности точки
называется бесконечно малой функцией (б.м.ф.) в окрестности точки 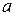 .
.
Две б.м.ф.  и
и 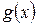 называются эквивалентными б.м.ф. в окрестности точки
называются эквивалентными б.м.ф. в окрестности точки 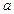 , если
, если 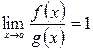 , и обозначают
, и обозначают  , при
, при 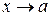 .
.
|
|
|
Стоит отметить, что предел отношения двух б.м.ф. не изменится, если каждую или одну из них заменить эквивалентной ей б.м.ф., т.е. если  и
и 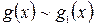 , то
, то
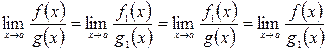 . (1.2)
. (1.2)
Приведем таблицу важнейших эквивалентностей при 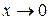
1. 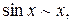
2. 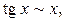
3. 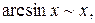
4. 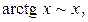
5. 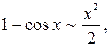
6. 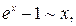
7. 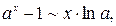
8. 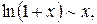
9. 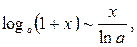
10. 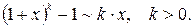
1.3 Неопределенность 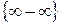 .
.
Если 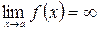 и
и 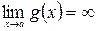 , то при вычислении
, то при вычислении 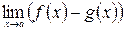 получим неопределённость
получим неопределённость 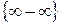 . Решая поставленную задачу необходимо при помощи алгебраических преобразований свести эту неопределённость к виду
. Решая поставленную задачу необходимо при помощи алгебраических преобразований свести эту неопределённость к виду 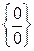 или
или 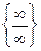 .
.
1.4 Неопределенность 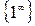 .
.
В этом случае наряду с уже рассмотренными методами можно применить так называемый второй замечательный предел:
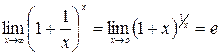 . (1.3)
. (1.3)
Дифференциальное исчисление функции одного переменного.
Производная функции.
Пусть функция 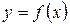 определена в некотором интервале (а;b). Возьмём произвольную точку
определена в некотором интервале (а;b). Возьмём произвольную точку 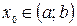 . Для любого
. Для любого 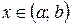 разность
разность 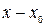 называется приращением аргумента х в точке
называется приращением аргумента х в точке 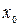 и обозначают Dх:
и обозначают Dх:
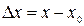 .
.
Разность 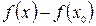 называется приращением функции
называется приращением функции  в точке
в точке 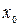 и обозначается Dу:
и обозначается Dу: 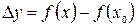 или
или 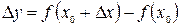 .
.
Производной функции 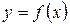 в точке
в точке 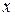 называется предел отношения приращения этой функции к приращению аргумента, когда последнее стремиться к нулю.
называется предел отношения приращения этой функции к приращению аргумента, когда последнее стремиться к нулю.
|
|
|
Обозначается: 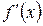 или
или 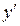 .
.
По определению
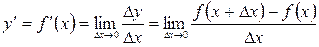 .
.
Функция в этом случае называется дифференцируемой в точке  .
.
Перечислим основные свойства производной.
Пусть  и
и 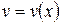 – дифференцируемые функции, а
– дифференцируемые функции, а 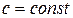 , тогда
, тогда
1.  .
.
2. 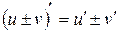 .
.
3. 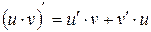 .
.
4. 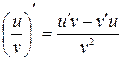 (
( 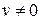 ).
).
Пусть 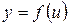 и
и 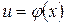 , тогда
, тогда 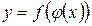 называется сложной функцией с промежуточным аргументом
называется сложной функцией с промежуточным аргументом 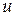 и независимой переменной
и независимой переменной 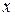 .
.
Если 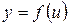 и
и 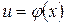 - дифференцируемые функции своих аргументов, то производная сложной функции
- дифференцируемые функции своих аргументов, то производная сложной функции 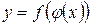 существует и находится по формуле
существует и находится по формуле
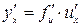 . (2.1)
. (2.1)
Таблица производных.
1. 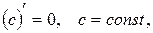
2. 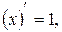
3. 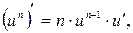
4. 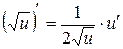
5. 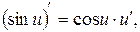
6. 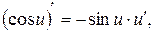
7. 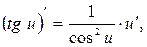
8. 
9. 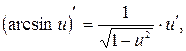
10. 
11. 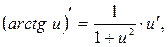
12. 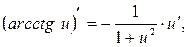
13. 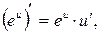
14. 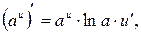
15. 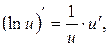
16. 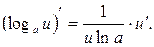
Если зависимость между аргументом 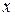 и функцией
и функцией 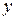 задана параметрически, т.е. в виде
задана параметрически, т.е. в виде 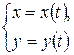 , то производная
, то производная 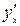 находится по формуле
находится по формуле
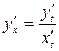 . (2.2)
. (2.2)
Если функция 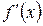 дифференцируема, то ее производная называется производной второго порядка от функции
дифференцируема, то ее производная называется производной второго порядка от функции 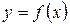 и обозначается
и обозначается 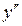 или
или 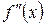 . Таким образом
. Таким образом
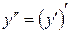 . (2.3)
. (2.3)
Производной 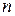 -го порядка называется производная от производной
-го порядка называется производная от производной 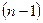 -го порядка и определяется формулой
-го порядка и определяется формулой
|
|
|
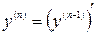 . (2.4)
. (2.4)
Если функция задана параметрически, т.е. 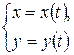 , то справедлива формула
, то справедлива формула
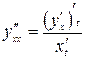 . (2.5)
. (2.5)
Дифференциал функции.
Дифференциалом функции 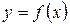 в точке
в точке 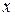 называется произведение производной функции на дифференциал независимой переменной, и обозначается
называется произведение производной функции на дифференциал независимой переменной, и обозначается 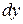 или
или  .
.
Таким образом
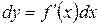 . (2.6)
. (2.6)
Сформулируем свойства дифференциалов.
Пусть 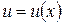 и
и 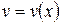 – дифференцируемые функции. Тогда
– дифференцируемые функции. Тогда
1. 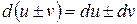 .
.
2. 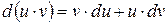 .
.
3.  .
.
4. Если 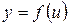 и
и 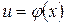 – дифференцируемые функции, то
– дифференцируемые функции, то  .
.
Дата добавления: 2021-01-21; просмотров: 170; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
