Приложение дифференциального исчисления.
Пусть дана функция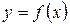 
и точка 
.
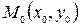Уравнение касательной к графику функции 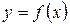в точке 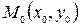имеет вид
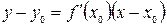. (2.7)
Уравнение нормали к графику функции 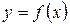в точке 
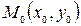имеет вид
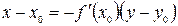. (2.8)
Дифференциальное исчисление используется и для нахождения приближённого значения функции. Если необходимо найти значение функции 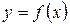в точке 
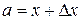, то
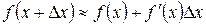. (2.9)
Исследование функции.
Монотонность функции.
Пусть функция 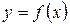непрерывна на интервале 
.
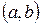Функция называется возрастающей на 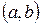, если для любых 
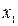и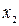 
из этого интервала, причём 
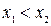выполняется условие 
.
Функция называется убывающей на 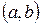, если для любых 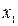и 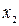из этого интервала, причём 
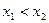выполняется условие 
.
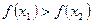Монотонность функции на интервале можно определить с помощью производной. Пусть функция 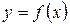дифференцируема на интервале 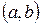. Тогда, если в каждой точке этого интервала 
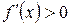, то функция возрастает, а если 
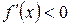, то функция убывает на этом интервале.
Экстремумы функции.
Точка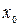 
называется точкой максимума функции 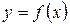, если существует окрестность точки 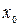, такая, что, для любого 
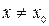из этой окрестности выполняется неравенство 
.
Точка 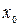называется точкой минимума функции 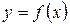, если существует окрестность точки 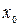, такая, что, для любого 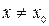из этой окрестности выполняется неравенство 
.
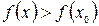Значение функции в точке минимума или максимума называется экстремумом функции.
|
|
|
Необходимое условие экстремума функции: если точка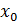 
– это точка локального экстремума функции 
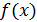, и существует производная в этой точке 
, то 
.
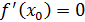Функция может иметь экстремум только в критических точках, т.е. в точках, в которых она определена, а её производная в них равна нулю или не существует.
Пусть 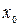критическая точка функции 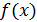. Если при переходе через неё (слева направо) производная функции меняет знак с 
на 
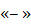, то 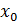– точка максимума, а если с 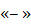на , то 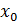– точка минимума.
Выпуклость, вогнутость. Точки перегиба.
График дифференцируемой функции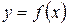 
называется выпуклым на 
, если он расположен выше любой её касательной на этом интервале.
График дифференцируемой функции 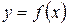называется вогнутым на , если он расположен ниже любой её касательной на этом интервале.
Точка графика непрерывной функции 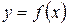, отделяющая его выпуклые и вогнутые части, называется точкой перегиба.
Промежутки выпуклости и вогнутости функции определяем при помощи производной второго порядка. Пусть функция 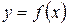определена во всех точках интервала 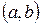. Тогда, если в каждой точке этого интервала 
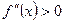, то график функции является выпуклым на , а если 
, для любого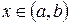 
, то график функции является вогнутым на .
|
|
|
Пусть в точке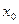 
вторая производная непрерывной функции 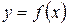равна нулю или не существует. Тогда, если при переходе через эту точку вторая производная меняет свой знак, то 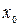– точка перегиба.
Асимптоты графика функции.
Асимптоты – это прямые к которым неограниченно приближается данная линия, когда её точка неограниченно удаляется от начала координат.
Асимптоты бывают вертикальными и наклонными.
Прямая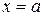 
является вертикальной асимптотой графика функции 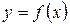, если 
.
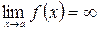Уравнение наклонной асимптоты графика функции 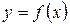имеет вид
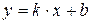, где 
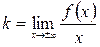и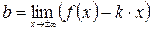 
. (3.1)
Дата добавления: 2021-01-21; просмотров: 149; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!