Текстовая задача и процесс ее решения
1. Структура текстовой задачи
Задача – это сформулированный словами вопрос, ответ на который требует выполнения арифметических действий.
Текстовая задача представляет собой описание какого-либо явления (ситуации, процесса). С этой точки зрения текстовая задача есть словесная модель явления (ситуации, процесса). И, как во всякой модели, в текстовой задаче описывается не все явление в целом, а лишь некоторые его стороны, главным образом, его количественные характеристики. Рассмотрим, например, такую задачу: «Автомобиль выехал из пункта А со скоростью 60 км/ч. Через 2 ч вслед за ним выехал второй автомобиль со скоростью 90 км/ч. На каком расстоянии от А второй автомобиль догонит первый?»
В задаче описывается движение двух автомобилей. Как известно, любое движение характеризуется тремя величинами: пройденным расстоянием, скоростью и временем движения. В данной задаче известны скорости первого и второго автомобилей (60 км/ч и 90 км/ч), известно, что они прошли одно и то же расстояние от пункта А до места встречи, количественную характеристику которого и надо найти. Кроме того, известно, что первый автомобиль был в пути на 2 ч больше, чем второй.
Обобщая, можно сказать, что текстовая задача есть описание на естественном языке некоторого явления (ситуации, процесса) с требованием дать количественную характеристику какого-либо компонента этого явления, установить наличие или отсутствие некоторого отношения между компонентами или определить вид этого отношения.
|
|
|
Чтобы выяснить, как построена текстовая задача рассмотрим следующий пример из начального курса математики:
«Свитер, шапку и шарф связали из 1 кг 200 г шерсти. На шарф потребовалась на 100 г шерсти больше, чем на шапку, и на 400 г меньше, чем на свитер. Сколько шерсти израсходовали на каждую вещь?»
В задаче речь идет о свитере, шапке и шарфе. Это объекты задачи. Относительно этих объектов имеются определенные утверждения и требования.
Утверждения:
1. Свитер, шапка и шарф связаны из 1200 г шерсти.
2. На шарф израсходовали на 100 г больше, чем на шапку.
3. На шарф израсходовали на 400 г меньше, чем на свитер.
Требования:
1. Сколько шерсти израсходовали на свитер?
2. Сколько шерсти израсходовали на шапку?
3. Сколько шерсти израсходовали на шарф? Утверждения задачи называют условиями (или условием,
как в начальной школе). В задаче обычно не одно условие, а несколько элементарных условий. Они представляют собой количественные или качественные характеристики объектов задачи и отношений между ними. Требований в задаче может быть несколько. Они могут быть сформулированы как в вопросительной, так и утвердительной форме. Условия и требования взаимосвязаны.
|
|
|
Систему взаимосвязанных условий и требований называют высказывательной моделью задачи.
Таким образом, чтобы понять, какова структура задачи, надо выявить ее условия и требования, отбросив все лишнее, второстепенное, не влияющее на ее структуру. Иными словами, надо построить высказывательную модель задачи.
Чтобы получить эту модель, надо текст задачи развернуть (сделать это можно письменно или устно), так как текст задачи, как правило, дается в сокращенном, свернутом виде. Для этого можно перефразировать задачу, построить ее графическую модель, ввести какие-либо обозначения и т.д.
Итак, составные части задачи: условие, вопрос, решение, ответ.
По отношению между условиями и требованиями различают:
а) определенные задачи - в них заданных условий столько, сколько необходимо и достаточно для выполнения требований;
б) недоопределенные задачи - в них условий недостаточно для получения ответа;
в) переопределенные задачи - в них имеются лишние условия.
В начальной школе недоопределенные задачи считают задачами с недостающими данными, а переопределенные - задачами с избыточными данными.
|
|
|
Например, задача «Возле дома росло 5 яблонь, 2 вишни и 3 березы. Сколько фруктовых деревьев росло возле дома?» является переопределенной, так как содержит лишнее условие.
Задача «Из зала вынесли сначала 12 стульев, потом еще 5. Сколько стульев осталось в зале?» является недоопределенной - в ней условий недостаточно, чтобы ответить на поставленный вопрос.
Уточним теперь смысл термина «решение задачи». Так сложилось, что этим термином обозначают разные понятия:
1) решением задачи называют результат, т.е. ответ на требование задачи;
2) решением задачи называют процесс нахождения этого результата, причем этот процесс рассматривают двояко: и как метод нахождения результата (например, говорят о решении задачи арифметическим способом) и как последовательность тех действий, которые выполняет решающий, применяя тот или иной метод (т.е. в данном случае под решением задачи понимается вся деятельность человека, решающего задачу).
2. Методы и способы решения текстовых задач
Основными методами решения текстовых задач являются арифметический и алгебраический. Кроме этого есть графический и практический.
Решить задачу арифметическим методом - это значит найти ответ на требование задачи посредством выполнения арифметических действий над числами.
|
|
|
Одну и ту же задачу можно решить различными арифметическими способами. Они отличаются друг от друга логикой рассуждений, выполняемых в процессе решения задачи.
Решим, например, различными арифметическими способами такую задачу: «Сшили 3 платья, расходуя на каждое по 4 м ткани. Сколько кофт можно было сшить из этой ткани, если расходовать на одну кофту 2 м?»
1 способ
1)4 ∙ 3= 12 (м) - столько было ткани;
2) 12:2 = 6 (кофт) - столько кофт можно сшить из 12 м ткани.
2 способ
1)4:2 = 2 (раза) - во столько раз больше идет ткани на платье, чем на кофту;
2) 3 ∙ 2 = 6 (кофт) - столько кофт можно сшить.
Решить задачу алгебраическим методом - это значит найти ответ на требование задачи, составив и решив уравнение или систему уравнений.
Если для одной и той же задачи можно составить различные уравнения (системы уравнений), то это означает, что данную задачу можно решить различными алгебраическими способами.
Например, задачу о массе шерсти, израсходованной на свитер, шапку и шарф (с. 115), можно решить тремя различными способами.
1 способ
Обозначим через х (г) массу шерсти, израсходованной на шапку. Тогда на шарф будет израсходовано (х + 100) г, а на свитер ((х + 100) + 400) г. Так как на все три вещи израсходовано 1200 г, то можно составить уравнение
х + (х + 100) + ((х + 100) + 400) = 1200.
Выполнив преобразования, получим , что х = 200. Таким образом, на шапку было израсходовано 200 г, на шарф -300 г, так как 200+ 100 = 300, на свитер - 700 г, так как (200+ 100)+ 400 = 700.
2 способ.
Обозначим через х (г) массу шерсти, израсходованной на шарф. Тогда на шапку будет израсходовано (х - 100) г, а на свитер - (х + 400) г. Поскольку на все три вещи израсходовано 1200 г, то можно составить уравнение:
х + (х-100) + (х + 400)= 1200.
Выполнив преобразования, получим, что х = 300. Таким образом, если на шарф израсходовали 300 г, то на шапку 200 г (300 - 100 = 200), а на свитер 700 г (300 + 400 = 700).
3 способ.
Обозначим через х (г) массу шерсти, израсходованной на свитер. Тогда на шарф будет израсходовано (х - 400) г, а на шапку (х - 400 - 100) г. Поскольку на все три вещи израсходовано 1200 г, то можно составить уравнение:
х + (х - 400) + (х - 500) = 1200.
Выполнив преобразования, получим, что х = 700. Таким образом, если на свитер израсходовано 700 г, то на шарф пошло
300 г (700 - 400 = 300), а на шапку - 200 г (700 - 400 - 100 = 200).
3. Этапы решения задачи и приемы их выполнения
Деятельность по решению задачи арифметическим методом включает следующие основные этапы:
1.Анализ задачи.
2.Поиск плана решения задачи.
3.Осуществление плана решения задачи.
4.Проверка решения задачи.
В реальном процессе решения задачи названные этапы не имеют четких границ и не всегда выполняются одинаково полно. Все зависит от уровня знаний и умений решающего.
1). Анализ задачи
Основное назначение этого этапа - понять в целом ситуацию, описанную в задаче; выделить условия и требования; назвать известные и искомые объекты, выделить все отношения (зависимости) между ними.
Вопросы для анализа задачи.
- О чем задача?
- Что требуется найти в задаче?
- Что обозначают те или иные слова в тексте задачи?
- Что в задаче неизвестно?
- Что является искомым?
Большую помощь в осмыслении задачи оказывает прием - перефразировка текста задачи. Он заключается в замене данного в задаче описания некоторой ситуации другим, сохраняющим все отношения, связи, качественные характеристики, но более явно их выражающим. Это достигается в результате отбрасывания несущественной, излишней информации, замены описания некоторых понятий соответствующими терминами и, наоборот, замены некоторых терминов описанием содержания соответствующих понятий; преобразование текста задачи в форму, удобную для поиска плана решения. Составляется краткая запись задачи.
Виды кратких записей:
1) краткая запись в виде таблицы.
2) краткая запись с помощью опорных слов
3) краткая запись с помощью чертежа
Например. 1. Таблица
| Скорость | Время |  Расстояние
| |
| 1 | 4 км/ч | 2 ч | ? км ? км |
| 2 | 5 км/ч | 2 ч | ? км |
2. С опорными словами
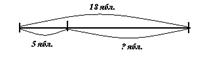Было – 18 ябл.
Съели – 5 ябл.
Осталось - ? ябл.
3.С помощью чертежа
После построения вспомогательной модели необходимо проверить:
1) все ли объекты задачи показаны на модели;
2) все ли отношения между объектами отражены;
3) все ли числовые данные приведены;
4) есть ли вопрос (требование) и правильно ли он указывает искомое?
2). Поиск и составление плана решения задачи
Назначение этого этапа: установить связь между данными и исходными объектами, наметить последовательность действий.
Поиск плана решения задачи является трудным процессом, который точно не определен. Можно только указать некоторые приемы, которые позволят осуществлять этот этап. Одним из наиболее известных приемов поиска плана решения задачи арифметическим способом является разбор задачи по тексту или по ее вспомогательной модели.
Разбор задачи проводится в виде цепочки рассуждений, которая может начинаться от данных задачи, так и от ее вопросов.
При разборе задачи от данных к вопросу решающий выделяет в тексте задачи два данных и на основе знания связи между ними (такие знания должны быть получены при анализе задачи) определить, какое неизвестное может быть найдено по этим данным и с помощью какого арифметического действия. Затем, считая это неизвестное данным, решающий вновь выделяет два взаимосвязанных данных, определяет неизвестное, которое может быть найдено по ним и с помощью какого действия и т.д., пока не будет выяснено, какое действие приводит к получению искомого в задаче объекта.
Проведем такой разбор по тексту задачи:
«На поезде, который шел со скоростью 56 км/ч, турист проехал 6 ч. После этого ему осталось проехать в 4 раза больше, чем проехал. Каков весь путь туриста?»
Рассуждения ведем от данных к вопросу: известно, что 6 ч турист проехал на поезде, который шел со скоростью 56 км/ч; по этим данным можно узнать расстояние, которое проехал турист за 6 ч, - для этого достаточно скорость умножить на время. Зная пройденную часть расстояния и то, что оставшееся расстояние в 4 раза больше, можно найти, чему оно равно. Для этого пройденное расстояние нужно умножить на 4 (увеличить в 4 раза). Зная, сколько километров турист проехал и сколько ему осталось ехать, можем найти весь путь, выполнив сложение найденных отрезков пути. Итак, первым действием будем находить расстояние, которое турист проехал на поезде; вторым действием - расстояние, которое ему осталось проехать; третьим - весь путь.
При разборе задачи от вопроса к данным нужно обратить внимание на вопрос задачи и установить (на основе информации, полученной при анализе задачи), что достаточно узнать для ответа на этот вопрос. Для чего нужно обратиться к условиям и выяснить, есть ли для этого необходимые данные. Если таких данных нет или есть только одно данное, то установить, что нужно знать, чтобы найти недостающее данное (недостающие данные), и т.д. Потом составляется план решения задачи. Рассуждения при этом проводятся в обратном порядке.
Проведем такой разбор той же задачи о движении туриста, строя цепочку рассуждений от вопроса к данным: «В задаче требуется узнать весь путь туриста. Мы установили, что путь состоит из двух частей. Значит, для выполнения требования задачи достаточно знать, сколько километров турист проехал и сколько километров ему осталось проехать. И то, и другое неизвестно. Чтобы найти пройденный путь, достаточно знать время и скорость, с которой ехал турист. Это в задаче известно. Умножив скорость на время, узнаем путь, который турист проехал. Оставшийся путь можно найти, увеличив пройденный путь в 4 раза (умножив на 4). Итак, вначале можно узнать пройденный путь, затем оставшийся, после чего сложением найти весь путь».
Поиск плана решения задачи может проводиться по вспомогательной модели, выполненной при анализе задачи.
Еще один способ разбора задачи – с помощью наводящих вопросов. Этот способ применяется при решении задач на нахождение неизвестного по двум разностям.
3). Осуществление плана решения задачи
Назначение данного этапа - найти ответ на требование задачи, выполнив все действия в соответствии с планом.
Для текстовых задач, решаемых арифметическим способом, используются следующие приемы:
- запись по действиям (с пояснением, без пояснения, с вопросами);
- запись в виде выражения.
Приведем примеры различных записей плана решения задачи: «На поезде, скорость которого 56 км/ч, турист проехал 6 ч. После этого ему осталось проехать в 4 раза больше, чем он проехал. Каков весь путь туриста?»
1. Запись решения по действиям с пояснением к каждому выполненному действию.
1) 56 ∙ 6 = 336 (км) - турист проехал за 6 ч
2) 336 ∙ 4= 1344 (км) - осталось проехать туристу
3) 336 + 1344 = 1680 (км) - должен был проехать турист.
Если пояснения даются в устной форме (или совсем не даются), то запись будет следующей:
1) 56 ∙ 6 = 336 (км)
2) 336 ∙ 4 = 1344 (км)
3) 336 + 1344 = 1680 (км)
2. Запись решения по действиям с вопросами:
1) Сколько километров проехал турист на поезде? 56 ∙ 6 = 336 (км)
2) Сколько километров осталось проехать туристу? 336 ∙ 4= 1344 (км)
3) Сколько километров турист должен был проехать? 336 + 1344= 1680 (км)
3. Запись решения в виде выражения.
Запись решения в этой форме осуществляется поэтапно. Сначала записываются отдельные шаги в соответствии с планом, затем составляется выражение и находится его значение. Так как обычно это значение записывают, поставив после числового выражения знак равенства, то запись становится числовым равенством, в левой части которого-выражение, составленное по условию задачи, а в правой - его значение, оно-то и позволяет сделать вывод о выполнении требований задачи.
Так, для рассматриваемой задачи эта форма записи имеет вид: 56 • 6 (км) - расстояние, которое проехал турист на поезде за 6 ч
56 ∙ 6 ∙ 4 (км) - расстояние, которое осталось проехать туристу 56-6 + 56-6-4 (км) - путь, который должен проехать турист 56 ∙ 6 + 56 ∙ 6 ∙ 4= 1680 (км)
Пояснения к действиям можно не записывать, а давать их в устной форме. Тогда запись решения задачи примет вид: 56 ∙ 6 + 56 ∙ 6 ∙ 4= 1680 (км)
4). Проверка решения задачи
Назначение данного этапа - установить правильность или ошибочность выполнения решения.
Известно несколько приемов, помогающих установить, верно ли решена задача. Рассмотрим основные.
1. Установление соответствия между результатом и условиями задачи.
Для этого найденный результат вводится в текст задачи и на основе рассуждений устанавливается, не возникает ли при этом противоречия.
Проверим, используя данный прием, правильность решения задачи о движении туриста.
Мы установили, что турист должен был всего проехать 1680 км. Пусть теперь этот результат будет одним из данных задачи. Далее, как известно, за 6 ч турист проедет 336 км (56 ∙ 6 = 336) и ему останется проехать 1680-336 = 1344(км). Согласно условию задачи это расстояние должно быть в 4 раза больше того, которое турист проехал на поезде за 6 ч. Проверим это, разделив 1344 на 336. Действительно, 1344:336 = 4. Следовательно, если найденный результат подставить в условие задачи, то противоречий с другими данными, а именно отношением «быть больше в 4 раза», не возникает. Значит, задача решена верно.
Заметим, что при использовании данного приема проверяются все отношения, имеющиеся в задаче, и если устанавливается, что противоречия не возникает, то делают вывод о том, что задача решена верно.
2. Решение задачи другим способом.
Пусть при решении задачи каким-то способом получен некоторый результат. Если ее решение другим способом приводит к тому же результату, то можно сделать вывод о том, что задача была решена верно.
Заметим, что если задача решена первоначально арифметическим способом, то правильность ее решения можно проверить, решив задачу алгебраическим методом.
Не следует также думать, что без проверки нет решения текстовой задачи. Правильность решения обеспечивается прежде всего четкими и логичными рассуждениями на всех других этапах работы над задачей.
3. Прикидка (прогнозирование с некоторой степенью точности правильности результата решения)
4. Составление обратной задачи.
5. Моделирование в процессе решения текстовых задач
Чтобы решить такую задачу, надо перевести ее на язык математических действий, т.е. построить ее математическую модель.
Вообще, математическая модель - это описание какого-либо реального процесса на языке математических понятий формул и отношений.
Математической моделью текстовой задачи является выражение (либо запись по действиям), если задача решаете) арифметическим методом, и уравнение (либо система уравнений), если задача решается алгебраическим методом.
В процессе решения задачи четко выделяются три этап; математического моделирования:
I этап - это перевод условий задачи на математический язык; при этом выделяются необходимые для решения данные и искомые и математическими способами описываются связи между ними;
II этап - внутримодельное решение (т.е. нахождение значения выражения, выполнение действий, решение уравнения);
| I |
III этап - интерпретация, т.е. перевод полученного решения на тот язык, на котором была сформулирована исходная задача. Проиллюстрируем сказанное на примере решения алгебраическим методом следующей задачи: «В одном вагоне электропоезда было пассажиров в 2 раза больше, чем в другом. Когда из первого вагона вышли 3 человека, а во второй вагон вошли 7 человек, то в обоих вагонах пассажиров стало поровну. Сколько пассажиров было в каждом вагоне первоначально?»
Обозначим через х первоначальное число пассажиров во втором вагоне. Тогда число пассажиров в первом вагоне - 2х. Когда из первого вагона вышли 3 человека, в нем осталось 2х - 3 пассажира. Во второй вагон вошли 7 человек, значит, в нем стало х + 7 пассажиров. Так как в обоих вагонах пассажиров стало поровну, то можно записать, что 2х - 3 = х + 7. Получили уравнение- это математическая модель данной задачи.
Следующий этап - решение полученного уравнения вне зависимости от того, - что в нем обозначает переменная х: переносим в левую часть члены уравнения, содержащие х, а в правую - не содержащие х, причем у переносимых членов знаки меняем на противоположные: 2х - х = 7 + 3. Приводим подобные члены и получаем, что х = 10.
Последний, третий этап - используем полученное решение, чтобы ответить на вопрос задачи: во втором вагоне было первоначально 10 человек, а в первом - 20 (10-2 = 20).
Наибольшую сложность в процессе решения текстовой задачи представляет перевод текста с естественного языка на математический, т.е. I этап математического моделирования. Чтобы облегчить эту процедуру, строят вспомогательные модели - схемы, таблицы и др. Тогда процесс решения задачи можно рассматривать как переход от одной модели к другой: от словесной модели реальной ситуации, представленной в задаче, к вспомогательной (схемы, таблицы, рисунки и т.д.); от нее - к математической, на которой и происходит решение задачи.
Графические модели используются, как правило, л обобщенного, схематического воссоздания ситуации : дачи. К графическим следует отнести следующие виды моделей:
1) рисунок;
2) условный рисунок;
3) чертеж;
4) схематичный чертеж (или просто схема).
Чертеж как графическая модель выполняется при помощи чертежных инструментов с соблюдением заданных отношений.
Схематический чертеж (схема) может выполняться от руки, на нем указываются все данные и искомые.
Знаковые модели могут быть выполнены как на естественном языке, так и на математическом языке. К знаковым моделям, выполненным на естественном языке, можно отнести краткую запись задачи, таблицы.
Знаковыми моделями текстовых задач, выполненными на математическом языке, являются: выражение, уравнение, система уравнений, запись решения задачи по действиям. Поскольку на этих моделях происходит решение задачи, их называют решающими моделями. Остальные модели, все схематизированные и знаковые, выполненные на естественном языке, - это вспомогательные модели, которые обеспечивают переход от текста задачи к математической модели.
Дата добавления: 2021-01-21; просмотров: 1556; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!