Понятие высказывательной формы (предиката). Операции над предикатами
Рассмотрим предложения с переменными:
1) x < 10
2) х + 1 = 7
3) число х делится на 5 без остатка
4) х – у = 2
5) х + у – z = 0
Все это повествовательные предложения, содержащие одну или несколько переменных. Если вместо переменных подставлять конкретные значения, то будем получать истинные или ложные высказывания.
Определение. Предложение, содержащее одну или несколько переменных, и которое при конкретных значениях переменных является высказыванием, называется высказывательной формой или предикатом.
Виды предикатов:
1) одноместные, примеры 1-3.
2) Двухместные, пример 4.
3) Трехместные, пример 5 и т.д.
С каждым предикатом связано два множества: область определения и множество истинности.
Область определения предиката – это множество значений переменных, при которых предикат превращается в высказывание, обозначается буквой Х.
Множество истинности предиката – это множество значений переменных, при которых предикат превращается в истинное высказывание, обозначается буквой Т. Т 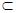 Х.
Х.
Обозначение предикатов: А(х): «x < 10», В(х, у): «х – у = 2», С(х, у, z): «х + у – z = 0».
Примерами предикатов в начальной школе являются неравенства и уравнения, слово «предикат не используется».
Способы превращения предиката в высказывание:
1) Вместо переменной подставить ее значение.
2) Использование специальных слов – кванторов: «каждый», «всякий», «любой» и др. – квантор общности (обозначают значком 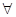 ), «существует», «найдется», «какой-нибудь» - квантор существования (обозначают значком
), «существует», «найдется», «какой-нибудь» - квантор существования (обозначают значком 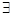 ).
).
|
|
|
Над предикатами выполняют такие же операции как и над высказываниями: отрицание, конъюнкция, дизъюнкция, импликация и эквиваленция.
Пусть на множестве Х заданы предикаты А(х) и В(х).
Предикат вида 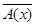 называется отрицанием предиката А(х).
называется отрицанием предиката А(х).
Предикат вида А(х) ∧ В(х) называется конъюнкцией предикатов А(х) и В(х).
Предикат вида А(х) ∨ В(х) называется дизъюнкцией предикатов А(х) и В(х).
Предикат вида А(х) ⇒ В(х) называется импликацией предикатов А(х) и В(х).
Предикат вида А(х) ⇔ В(х) называется эквиваленцией предикатов А(х) и В(х).
Пусть А – множество истинности предиката А(х), В – множество истинности предиката В(х),
1) Множество истинности отрицания предиката А(х) вычисляем по формуле: Т1 = 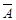
2) Множество истинности конъюнкции предикатов А(х) ∧ В(х) вычисляем по формуле: Т2 = А∩В.
3) Множество истинности дизъюнкции предикатов А(х) ∨ В(х) вычисляем по формуле: Т3 = А 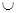 В.
В.
4) Множество истинности импликации предикатов А(х) ⇒ В(х) вычисляем по формуле: Т4 = 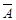
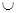 В.
В.
Если множество истинности предиката А(х) является подмножеством множества истинности предиката В(х), то из предиката А(х) логически следует предикат В(х). При этом предикат А(х) называется достаточнымусловием, а В(х) – необходимым условием.
|
|
|
Например, пусть на множестве Х = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} заданы предикаты А(х): «х кратно 4», В(х): «х кратно 2». Найдем множества истинности этих предикатов: ТА = {4, 8} – множество истинности предиката А(х), ТВ ={ 2, 4, 6, 8, 10} – множество истинности предиката В(х). Замечаем, что множество истинности первого предиката является подмножеством множества истинности второго предиката, в этом случае говорят, что из предиката А(х) логически следует предикат В(х). Импликацию А(х)⇒ В(х): «если х кратно 4, то х кратно 2» можно переформулировать так: «для того чтобы число х делилось на 4, необходимо, чтобы оно делилось на 2» и «для того чтобы число х делилось на 2, достаточно, чтобы оно делилось на 4».
Теорема
Определение теоремы
Теорема – это высказывание, истинность которого устанавливается при помощи доказательства.
Примеры теорем:
· Из алгебры. 1) если а > b, b > с, то а > с. 2) признаки делимости, например, для того чтобы натуральное число делилось на 10, необходимо и достаточно, чтобы его десятичная запись оканчивалась на 0.
· Из геометрии. Теорема Пифагора: если треугольник прямоугольный, то квадрат гипотенузы равен сумме квадратов катетов.
|
|
|
Строение теоремы.
Рассмотрим теорему: «Если сумма цифр натурального числа делится на 9,то и само число делится на 9».
Выделим условие теоремы (текст, стоящий между словами «если» и «то»): А(х): «сумма цифр натурального числа делится на 9», заключение (текст, стоящий после слова «то»): В(х): «число делится на 9».
Общий вид теоремы в условной форме (со словами «если…, то…»): ( 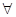 х
х 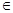 N) А(х) ⇒ В(х).
N) А(х) ⇒ В(х).
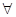 х
х 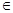 N – разъяснительная часть теоремы (она не всегда присутствует в явном виде, но подразумевается всегда).
N – разъяснительная часть теоремы (она не всегда присутствует в явном виде, но подразумевается всегда).
А(х) – условие теоремы.
В(х) – заключение теоремы.
Если теорема записана не в виде импликации, то нужно ее переформулировать в вид импликации, т.е. со словами«если…, то…».
Например, рассмотрим теорему «В прямоугольнике диагонали равны». Переформулируем ее так: «Если четырехугольник – прямоугольник, то его диагонали равны». Тогда условие теоремы «четырехугольник – прямоугольник», а заключение «диагонали четырехугольника равны». Речь идет о четырехугольниках, поэтому Х – множество четырехугольников.
Виды теорем:
1) Данная. Например, «Если четырехугольник – прямоугольник, то его диагонали равны».
|
|
|
В общем виде: ( 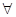 х
х 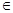 Х) А(х) ⇒ В(х).
Х) А(х) ⇒ В(х).
2) Обратная. Например, «Если диагонали четырехугольника равны, то это – прямоугольник» (в данной теореме поменяли местами условие и заключение).
В общем виде: ( 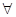 х
х 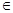 Х) В(х) ⇒ А(х).
Х) В(х) ⇒ А(х).
3) Противоположная. Например, «Если четырехугольник – не прямоугольник, то его диагонали не равны» (условие и заключение данной теоремы заменили отрицаниями).
В общем виде: ( 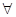 х
х 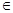 Х)
Х) 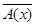 ⇒
⇒ 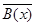 .
.
4) Обратная противоположной (в противоположной теореме поменяли местами условие и заключение) или противоположная обратной (в обратной теореме условие и заключение заменили их отрицаниями). Например, «Если диагонали четырехугольника не равны, то это – не прямоугольник».
В общем виде: ( 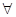 х
х 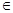 Х)
Х) 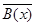 ⇒
⇒ 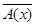 .
.
Применение теорем в математике.
Свойства основных понятий раскрываются в аксиомах.
Аксиома – предложение, принимаемое без доказательства.
Доказываемые свойства называют в геометрии: теоремами, следствиями, признаками; в алгебре: формулами, тождествами, правилами.
4.1.4. Математические доказательства
1. Умозаключения и их виды
В логике вместо термина «рассуждения» чаще используются (как его синоним) слово «умозаключение», им и будем пользоваться.
Умозаключение - это способ получения нового знания на основе некоторого имеющегося.
Умозаключение состоит из посылок и заключения.
Посылки - это высказывания, содержащие исходное знание.
Заключение - это высказывание, содержащее новое знание, полученное из исходного.
В умозаключении из посылок выводится заключение.
Рассмотрим примеры умозаключений, которые выполняют младшие школьники, изучая математику.
Пример 1. Ученику предлагается объяснить, почему число 23 можно представить в виде суммы 20 + 3. Он рассуждает: «Число 23 - двузначное. Любое двузначное число можно представить в виде суммы разрядных слагаемых. Следовательно, 23 = 20 + 3».
Первое и второе предложения в этом умозаключении посылки, причем одна посылка общего характера - это высказывание «любое двузначное число можно представить в виде суммы разрядных слагаемых», а другая - частная, она характеризует только число 23 - оно двузначное. Заключение - это предложение, которое стоит после слова «следовательно», - также носит частный характер, так как в нем речь идет о конкретном числе 23.
Пример 2. Один из приемов ознакомления младших школьников с переместительным свойством умножения заключается в следующем. Используя различные средства наглядности, школьники вместе с учителем устанавливают, что 6 ∙ 3 = 3 ∙ 6, 5 ∙ 2 = 2 ∙ 5, 3 ∙ 7 = 7 ∙ 3. А затем, на основе полученных равенств делают вывод: для всех натуральных чисел а и b верно равенство а ∙ b =b ∙ а.
В данном умозаключении посылками являются первые три равенства, в них утверждается, что для конкретных натуральных чисел выполняется такое свойство. Заключением в данном примере является утверждение общего характера - переместительное свойство умножения натуральных чисел.
Видим, что умозаключения бывают разные. В примере 1 заключение логически следует из посылок, и мы не сомневаемся в его истинности. Такие умозаключения называют в логике дедуктивными.
| I |
Определение. Дедуктивным называется умозаключение, в котором посылки и заключение находятся в отношении логического следования.
Если посылки дедуктивного умозаключения обозначить буквами А1, А2, ... , Аn, а заключение - буквой В, то схематично само умозаключение можно представить так: А1, А2,…,Ап => В.
А1, А2,…, А n
Часто используют такую запись: B В ней черта заменяет слово «следовательно».
В примере 1 рассмотрено дедуктивное умозаключение. В дедуктивном умозаключении всегда, когда истинны посылки, истинно и заключение.
Умозаключение, которое рассмотрено в примере 2, отлично от первого. В нем приведены три посылки частного характера, которые показывают, что некоторые натуральные числа обладают свойством: от перестановки множителей произведение не изменяется. И на этой основе сделан вывод, что этим свойством обладают все натуральные числа. Такие умозаключения называют неполной индукцией.
Определение. Неполная индукция- это умозаключение, в котором на основании того, что некоторые объекты класса обладают определенным свойством, делается вывод о том, что этим свойством обладают все объекты данного класса.
Неполная индукция не является дедуктивным умозаключением, поскольку, рассуждая по такой схеме, можно прийти к ложному выводу.
Вообще к выводам, полученным с помощью неполной индукции, надо относиться критически, так как они носят характер предположения, гипотезы и нуждаются в дальнейшей проверке: их надо либо доказать, либо опровергнуть.
Несмотря на то что неполная индукция не всегда приводит к истинным выводам, роль таких умозаключений в процессе познания велика. Почти все общие положения и, в частности, научные законы являются результатом умозаключений, называемых неполной индукцией.
Существует еще один пример рассуждений - по аналогии.
Слово «аналогия» в переводе с греческого означает «соответствие, сходство».
Вообще под аналогией понимают умозаключение, в котором на основании сходства двух объектов в некоторых признаках и при наличии дополнительного признака у одного из них делается вывод о наличии такого же признака у другого объекта.
Аналогия помогает открывать новые знания, способы деятельности или использовать усвоенные способы деятельности в измененных условиях.
Вывод по аналогии носит характер предположения, гипотезы и поэтому нуждается либо в доказательстве, либо в опровержении.
Например, ученик установил, что число делится на 6, если оно делится на 2 и на 3. Затем, действуя по аналогии, сделал вывод: число делится на 8, если оно делится на 2 и на 4. Чтобы убедиться в ложности полученного вывода, достаточно привести контрпример: число 12 делится на 2 и на 4, но не делится на 8.
Широко используется аналогия в обучении математике младших школьников. Это происходит при изучении свойств объектов, отношений между ними и действий с ними. Приведем несколько примеров.
Аналогию можно использовать для «открытия» новых свойств изучаемых объектов. Например, если при изучении классов установлено, что в классе единиц три разряда - единицы, десятки, сотни, а в классе тысяч также три разряда-единицы тысяч, десятки тысяч, сотни тысяч, то вывод о числе разрядов в классе миллионов и их названии дети могут сделать самостоятельно, по аналогии.
Аналогия может быть использована для установления отношений между данными объектами. Например, учащиеся установили, что 4(3 + 7) > 4 ∙ 3 + 4 ∙ 6, так как 4 ∙ (3 + 7) = 4 ∙ 3 + 4 ∙ 7, а 4 ∙ 7 > 4 ∙ 6. Рассматривая затем выражения 3 ∙ (8 + 9) и 3 ∙ 8 + 3 ∙ 7, учащиеся могут по аналогии сделать вывод о том, что 3 ∙ (8 + 9) > 3 ∙ 8 + 3 ∙ 7. Проверить его правильность можно либо путем рассуждений, аналогичных тем, что проводились при выполнении первого задания, либо при помощи вычислений.
Аналогия может быть использована и для выводов о способе действия на основе изучения другого способа. Так, после рассмотрения способа умножения двузначного числа на однозначное на примере умножения 27 на 3 (27 ∙ 3 = (20 + 7) ∙ 3 = 20 ∙ 3 + 7 ∙ 3 = 81) детям предлагается умножить 712 на 4. Действуя по аналогии, они устанавливают, что 712 ∙ 4 = (700+10 + 2) 4 = 2800 + 40 + 8 = 2848. Далее по аналогии устанавливают, как умножить 6288 на 3.
Следующим шагом может быть обобщение, т.е. получение правила умножения многозначного числа на однозначное, т.е. использование неполной индукции.
2. Схемы дедуктивных умозаключений
Рассмотрим подробнее дедуктивные (правильные) умозаключения. Согласно определению (п. 1), в дедуктивном умозаключении посылки и заключение находятся в отношении логического следования. Это означает, что в нем всегда из истинных посылок следует истинное заключение.
В логике считают, что правильность умозаключения определяется его формой и не зависит от конкретного содержания входящих в него утверждений. И в логике эти правила называют правилами вывода или схемами дедуктивных (правильных) умозаключений. Правил много, но наиболее часто используются следующие: А(х)=>В(х), А(а) - правило заключения;
В(а)
А(х) => В(х), 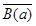 - правило отрицания;
- правило отрицания;
А(а)
А(х) => В{х), В{х) => С(х) - правило силлогизма.
А(х) => С(х)
Выясним, что обозначают все знаки, использованные в записи этих правил; как их применять на практике.
Рассмотрим, например, правило заключения. В нем обозначены две посылки А(х) => В(х) и А(а). Первую называют общей посылкой, это может быть теорема, определение и, вообще, предложение вида А(х) => В(х). Вторую посылку А (а) называют частной, она получается из условия А(х) при х = а. Предложение В(а) - это заключение, оно получается из В(х) при х = а. Посылки отделены от заключения чертой, которая заменяет слово «следовательно».
Приведем пример умозаключения, выполненного по правилу заключения:
Если запись числа х оканчивается цифрой 5, то число х делится на 5. Запись числа 135 оканчивается цифрой 5. Следовательно, число 135 делится на 5.
В качестве общей посылки в этом умозаключении выступает утверждение вида «если А(х), то В(х)», где А(х) - это «запись числа х оканчивается цифрой 5», а В(х)- «число х делится на 5». Частная посылка представляет собой высказывание, которое получилось из условия общей при х = 135 (т.е. это Л(135)). Заключение является высказыванием, полученным из В(х) при х = 135 (т.е. это 5(135)).
Приведем теперь пример умозаключения, выполненного по правилу отрицания.
Если запись числа х оканчивается цифрой 5, то число х делится на 5. Число 177 не делится на 5. Следовательно, оно не оканчивается цифрой 5.
Видим, что в этом умозаключении общая посылка такая же, как и в предыдущем, а частная представляет собой отрицание высказывания «число 177 делится на 5.
Заключение - это отрицание предложения «Запись числа 177 не оканчивается цифрой 5».
И, наконец, рассмотрим пример умозаключения, построенного по правилу силлогизма.
Если число х кратно 12, то оно кратно 6. Если число х кратно 6, то оно кратно 3. Следовательно, если число х кратно 12, то оно кратно 3.
В этом умозаключении две посылки вида «если А(х), то В(х)» и «если В(х), то С(х)», где А{х)- это предложение «х кратно 12», В(х) - предложение «х кратно 6» и С(х) - предложение «х кратно 3». Заключение представляет собой высказывание «если А (х), то С(х)».
3. Способы математического доказательства
В обыденной жизни часто, когда говорят о доказательстве, имеют в виду просто проверку высказанного утверждения. В математике проверка и доказательство - это разные вещи, хотя и связанные между собой. Пусть, например, требуется доказать, что если в четырехугольнике три угла прямые, то он - прямоугольник.
Если мы возьмем какой-либо четырехугольник, у которого три угла прямые, и, измерив четвертый, убедимся в том, что он действительно прямой, то эта проверка сделает данное утверждение более правдоподобным, но еще не доказанным.
Чтобы доказать данное утверждение, рассмотрим произвольный четырехугольник, в котором три угла прямые. Так как в любом выпуклом четырехугольнике сумма углов равна 360°, то и в данном она составляет 360°. Сумма трех прямых углов равна 270° (90° ∙3 = 270°), и, значит, четвертый имеет величину 90° (360°- 270° = 90°). Если все углы четырехугольника прямые, он - прямоугольник. Следовательно, данный четырехугольник будет прямоугольником. Что и требовалось доказать.
Заметим, что сущность проведенного доказательства состоит в построении такой последовательности истинных утверждений (теорем, аксиом, определений), из которых логически следует утверждение, которое нужно было доказать.
Вообще доказать какое-либо утверждение- это значит показать, что это утверждение логически следует из системы истинных и связанных с ним утверждений.
Основным способом математического доказательства является дедуктивный вывод. А само доказательство - это цепочка умозаключений, причем заключение каждого из них (кроме последнего) является посылкой в одном из последующих умозаключений.
Например, в приведенном выше доказательстве можно выделить следующие умозаключения:
1. В любом выпуклом четырехугольнике сумма углов равна 360°; данная фигура - выпуклый четырехугольник, следовательно, сумма углов в нем 360°.
2. Если известна сумма всех углов четырехугольника и сумма трех из них, то вычитанием можно найти величину четвертого; сумма всех углов данного четырехугольника равна 360°, сумма трех 270° (90° ∙3 = 270°), то величина четвертого 360° - 270° = 90°.
3. Если в четырехугольнике все углы прямые, то этот четырехугольник - прямоугольник; в данном четырехугольнике все углы прямые, следовательно, он прямоугольник.
Все приведенные умозаключения выполнены по правилу заключения и, следовательно, являются дедуктивными.
Математическое доказательство - это не просто набор умозаключений, это умозаключения, расположенные в определенном порядке.
По способу ведения различают прямые и косвенные доказательства. Рассмотренное ранее доказательство было прямым - в нем, основываясь на некотором истинном предложении и с учетом условия теоремы, строилась цепочка дедуктивных умозаключений, которая приводила к истинному заключению.
К прямым доказательствам в математике относят полную индукцию -такой способ доказательства, при котором истинность утверждения следует из истинности его во всех частных случаях.
Задача 1. Доказать, что каждое составное натуральное число, больше 4, но меньше 20, представимо в виде суммы двух простых чисел.
Решение. Вспомним определение простого и составного числа. Простым называется такое натуральное число, которое делится только на 1 и на себя. Числа 2, 13, 5, 17- простые. Числа, которые имеют более двух делителей, называются составными. Число 1 не является ни простым, ни составным.
В данной задаче рассматривается множество чисел, которые больше 4, но меньше 20. Составными в нем будут числа: 6, 8, 9, 10, 12, 14, 15, 16, 18. Каждое из них можно представить в виде суммы двух простых чисел: 6 = 3 + 3; 8 = 5 + 3; 9 = 7 + 2; 10 = 5+5 (или 7+3); 12 = 5+7; 14 = 11+3 (или 7+7); 15 = 13+2; 16 = 13 + 3 (или 11 + 5), 18 = 13 + 5 (или 11+7). Так как данное утверждение истинно во всех частных случаях, то оно доказано.
Примером косвенного доказательства является доказательство методом от противного. Сущность его состоит в следующем. Пусть требуется доказать теорему А => В. При доказательстве методом от противного допускают, что заключение теоремы (В) ложно, а, следовательно, его отрицание истинно. Присоединив предложение В к совокупности истинных посылок, используемых в процессе доказательства (среди которых находится и условие А), строят цепочку дедуктивных умозаключений до тех пор, пока не получится утверждение, противоречащее одной из посылок и, в частности, условию А. Как только такое противоречие устанавливают, процесс доказательства заканчивают и говорят, что полученное противоречие доказывает истинность теоремы А => В.
Задача 2. Доказать, что если а + 3 > 10, то а ≠ 7.
Решение. Предположим, что заключение данного утверждения ложно, тогда истинным будет его отрицание, т.е. предложение а = 7. Подставим это значение а в неравенство а + 3 > 10. Получим предложение 7 + 3 > 10 или 10 > 10, которое ложно. Пришли в противоречию с определением отношения «больше» для чисел. Следовательно, наше предположение неверное, и поэтому, если а + 3 > 10, то а ≠ 7.
Завершая обсуждение вопросов, связанных с математическим доказательством, выясним, как связаны между собой неполная индукция с дедуктивным выводом.
Ранее было отмечено, что выводы, которые мы получаем с помощью неполной индукции (или аналогии) носят характер предположения и поэтому их надо либо доказывать, либо опровергать. Поскольку выводы, о которых идет речь, носят, как правило, характер обобщения, то они формулируются в виде предложений, содержащих квантор общности. И следовательно, чтобы их опровергнуть, надо привести контрпример, а чтобы убедиться в истинности - доказать. Причем имеется в виду дедуктивный вывод. Таким образом, в процессе познания неполная индукция и математическое доказательство оказываются тесно связанными.
Дата добавления: 2021-01-21; просмотров: 964; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
