Декартово произведение множеств

Тема 4.1. Элементы логики

4.1.1.Множества и операции над ними (этот материал изучали на предмете «Математика» на первом курсе, давала лекцию по этой теме)

Основные понятия и определения

В русском языке для обозначения тех или иных совокупностей обычно используются различные слова. Например, говорят: стадо коров, табун лошадей, букет цветов, команда спортсменов, набор инструментов, коллекция марок и т.д. В математике стремятся к единообразию, и для обозначения совокупностей употребляется, как правило, единый термин – множество. Таким образом, множество рассматривается как совокупность предметов реального мира (или объектов нашей интуиции), обладающих общим свойством. Другими словами, множество – это совокупность предметов, сама рассматриваемая как один предмет. Дать определение множеству нельзя, можно лишь пояснить его.

Понятие множества является одним из основных понятий математики и поэтому не определяется через другие. Его можно пояснить на примерах. Так, можно говорить о множестве гласных букв русского алфавита, о множестве натуральных чисел, о множестве треугольников, множестве корней уравнения и т.д.

В разговорной речи термин «множество» всегда связывается с большим числом предметов. В теории множеств это не обязательно. Будем рассматривать и бесконечные множества, и множества, содержащие любое конечное число предметов, и даже множество, не содержащее ни одного предмета, - пустое множество (обозначают знаком ∅ ).

Объекты, из которых состоит множество, называют его элементами.

Произвольные множества обозначают заглавными буквами латинского алфавита: A, B, C, D, …, Z, A₁, A₂, …, A_n. Элементы множества обозначают строчными буквами латинского алфавита: a , b , c , d ,…, z , a ₁ , a ₂ ,…, a_n.

Отношение между элементами и множеством выражают словами: «является элементом» или «принадлежит». Предложение «Элемент a принадлежит множеству A» обозначают 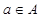. Если же a не является элементом множества A, то пишут .

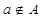Множества, элементами которых являются числа, называются числовыми. Для числовых множеств используют общепринятые обозначения:

N - множество натуральных чисел;

Z - множество целых чисел;

Q - множество рациональных чисел;

R - множество действительных чисел.

Способы задания множеств

Множество можно считать заданным, если о любом объекте можно сказать, принадлежит он этому множеству или не принадлежит.

Множество можно задать непосредственным перечислением всех его элементов в произвольном порядке. В этом случае названия всех элементов множества записывают в строку, отделяют запятыми и заключают в фигурные скобки. Каждый элемент записывают только один раз. Порядок перечисления его элементов не существенен.

Например, множество А, состоящее из всех цифр, можно записать так:

A = {1, 2, 3, 4, 5, 6, 7, 8, 9, 0};

Множество P букв, которые используют для записи слова «математика», записывают следующим образом:

P = {м, а, т, е, и, к}.

{1, 3, 7} и {3, 7, 1} - это одно и то же множество.

Перечислением элементов можно задать только конечное множество с небольшим числом элементов. Когда задать множество перечислением его элементов трудно или невозможно (в случае бесконечных множеств), то применяется другой способ задания множества через указание характеристического свойства его элементов.

Характеристическим свойством, определяющим множество, называется такое свойство, которым обладает каждый элемент, принадлежащий данному множеству, и не обладает ни один элемент, ему не принадлежащий.

Например, запись B = {x | x 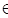Z, -2< x < 3} означает, что множество В состоит из целых чисел, больших -2 и меньших 3.

Второй способ более общий: он позволяет задавать и конечные, и бесконечные множества.

Часто одно и то же множество задано и первым, и вторым способами. Очень важно умение переходить от одного способа задания к другому.

Например, множество D натуральных чисел, меньших 7, заданное посредством указания характеристического свойства его элементов, можно задать и так: D = {1, 2, 3, 4, 5, 6}, т.е. перечислив все его элементы.

Также множества можно задать на числовой прямой (числовые) и на кругах Эйлера.

В начальном курсе математики понятия множества и элементов множества в явном виде не изучаются, но в силу их большой общности они, по существу, пронизывают всю начальную математику. Так, при выполнении задания «Запишите числа, которые больше 65 и меньше 75» ученики встречаются с двумя способами задания одной и той же совокупности чисел. Один способ – указано свойство чисел «быть больше 65 и меньше 75», другой – числа этой совокупности перечисляются: 66, 67, 68, 69, 70, 71, 72, 73, 74. Смысл упражнения – перейти от одного способа задания множества к другому. Аналогичные задачи приходится решать школьникам на других уроках, в частности на уроках русского языка: «Назовите все согласные буквы русского алфавита», «Подчеркните в данном упражнении все существительные», «Выпишите из текста все прилагательные» и т.д.

Два множества называют равными, если они состоят из одних и тех же элементов. Например, множества K = {1, 2, 3, 4} и L = {x | x 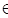N, x<5} равны.

Понятие подмножества

Рассмотрим множество A = {1, 2, 3, 4, 5, 6, 7, 8, 9}. Выделим из множества A те его элементы, которые являются простыми числами. Получим множество B = {2, 3, 5, 7}, все элементы которого являются элементами множества A. В этом случае говорят, что B – подмножество множества А.

Определение. Множество В называется подмножеством множества А, если каждый элемент множества В является элементом множества А. Обозначают .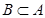

Например, множество натуральных чисел есть подмножество множества целых чисел.

Пустое множество считается подмножеством любого множества. Подмножество данного множества может и совпадать с данным множеством. Это непосредственно следует из определения подмножества данного множества.

Само множество и пустое множество называют несобственными подмножествами данного множества. Все остальные подмножества данного множества называют собственными.

Например. Составить все возможные подмножества множества K = {2, 3, 5}.

Несобственные: A = {5, 3, 2}, B = ∅.

Собственные: C = {5; 2}, D = {5; 3}, E = {2, 3}, F = {5}, M = {3}, P = {2}.

Отношения между множествами

Об отношениях между множествами судят по количеству общих элементов этих множеств.

Отметим две возможности.

I. Множества А и В не имеют общих элементов. На диаграммах Эйлера-Венна нет точек (элементов), которые принадлежали бы одновременно А и В (рисунок 1).

II. Множества А и В имеют общие элементы, т.е. существуют элементы, которые одновременно принадлежат и множеству А, и множеству В. При этом возможны три случая.

1. Не все элементы множества А принадлежат множеству В, и не все элементы множества В принадлежат множеству А. В этом случае говорят, что множества А и В находятся в отношении пересечения. Кругами Эйлера это отношение изображается так, как показано на рисунке 2.

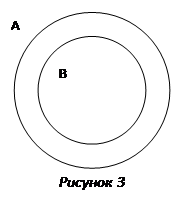
2. Все элементы множества В принадлежат множеству А, но множество А может содержать элементы, не принадлежащие множеству В. Множество В является подмножеством множества А. В этом случае говорят, что множества В и А находятся в отношении включения. Кругами Эйлера такое отношение изображено на рисунке 3.

3. Все элементы множества А принадлежат множеству В, и все элементы множества В принадлежат множеству А. В этом случае множества равны или совпадают (рисунок 4).

Операции над множествами

Объединение множеств

Определение. Объединением множеств А и В называется множество, состоящее из всех элементов, которые принадлежат хотя бы одному их этих множеств А или В.

Объединение множеств А и В обозначается символом .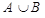

Аналогично определяется объединение трех и более множеств.

Пусть А={2; 5; 7}, В={3; 5; 6}. Тогда А 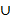В ={2; 3; 5; 6; 7}.

На рисунке изображено объединение множеств А и В с помощью кругов Эйлера. Вся заштрихованная область – это множество А 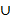В.

2. Пересечение множеств

Определение. Пересечением множеств А и В называется множество, состоящее только из тех элементов, которые принадлежат множеству А и множеству В одновременно.

Пересечение множеств А и В обозначают символом .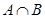

Аналогично определяется пересечение трех и более множеств.

Если множества А и В изобразить кругами Эйлера, то пересечению будет соответствовать заштрихованная часть.

Пусть А={2; 5; 7; 8}, В={3; 5; 6; 7} .Тогда А ∩В={5; 7}.

Разность двух множеств

Разностью множеств А и В называется множество, состоящее из тех элементов множества А, которые не принадлежат множеству В.

Разность множеств А и В обозначают символом А \ В.

Если множества А и В изобразить кругами Эйлера, то разности множеств соответствует заштрихованная часть.

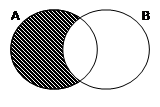
Пусть А={1; 2; 5; 7}, В={1; 3; 5; 6}. Тогда А\В ={2;7}, а В\А={3; 6}.

Если множество В является подмножеством множества А, то разность множеств А и В называется дополнением множества В до множества А.

Декартово произведение множеств

Понятие кортежа

В математике корте́ж - упорядоченный конечный набор букв, чисел, знаков.

Элементы кортежа могут повторяться в нём любое число раз (этим, в частности, он отличается от упорядоченного множества, куда каждый элемент может входить только в одном экземпляре).

Число компонент кортежа называется его длиной.

В математике кортеж обычно записывается перечислением элементов в круглых или угловых скобках.

Элементы кортежа называются его компонентами, или координатами.

Кортеж длины нуль называется пустым.

Два кортежа называются равными, если их длины равны и равны соответственные компоненты.

Частным случаем кортежа является упорядоченная пара.

Определение. Декартовым произведением множеств 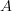и 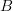называется множество всех упоядоченных пар, первая компонета которых приналежит множеству А, а вторая множеству В, т.е. .

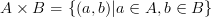Пример. Пусть 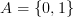, 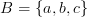. Тогда .

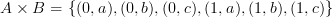Кое-какую интуицию относительно декартова произведения вероятно поможет развить иллюстрация в виде таблицы. Столбцы в ней отводятся для элементов одного множества, строки — для другого множества, а на пересечении стоит их декартово произведение:

А B	a	b	c
0	(0; a)	(0; b)	(0; c)
1	(1; a)	(1; b)	(1; c)

Число элементов множества

Если А – конечное множества, то в ряде случаев можем подсчитать число элементов, которые составляют множество А.

Это число обозначают так: n(A).

A = {12, 25, 47, 84}, n(A) = 4, т.е. множество А содержит 4 элемента.

4.1.2. Математические понятия

Дата добавления: 2021-01-21; просмотров: 552; Мы поможем в написании вашей работы!

Поделиться с друзьями:

12 3 4 Следующая ⇒

Мы поможем в написании ваших работ!