ОСНОВНЫЕ МЕТОДЫ ИНТЕГРИРОВАНИЯ
Метод непосредственного интегрирования
Метод интегрирования, при котором данный интеграл путём тождественных преобразований подынтегральной функции (или выражения) и применения свойств неопределённого интеграла приводится к одному или нескольким табличным, называется непосредственным интегрированием.
Замечание 1.
Под тождественными преобразованиями будем понимать:
- применение формул элементарной математики;
- почленное деление числителя подынтегрального выражения на знаменатель;
- дополнительные или искусственные преобразования, которые не нарушают равносильности выражения.
Интегрирование алгебраических функций
1 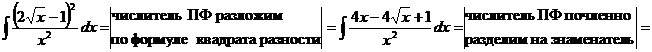
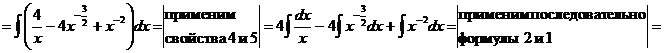

Выполните самостоятельно
2 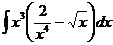 3
3 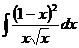 4
4 
5 
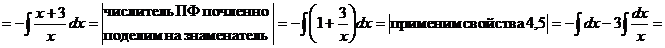
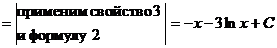
Выполните самостоятельно
6  7
7  8
8 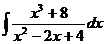
Указание. Примените формулу 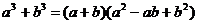
9 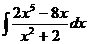 Указание. Числитель ПФ разложите на множители:
Указание. Числитель ПФ разложите на множители: 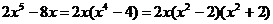
10 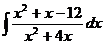 Указание. В числителе ПФ примените формулу:
Указание. В числителе ПФ примените формулу: 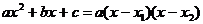
11 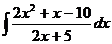 . 12
. 12  .
.
Указание. Числитель ПФ разложите на множители: 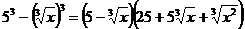
13 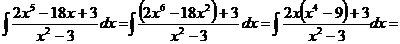
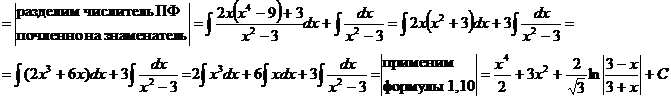
Интегрирование тригонометрических функций
14 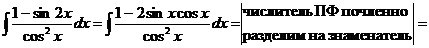
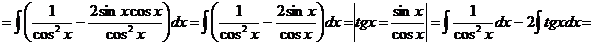
 .
.
15 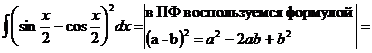
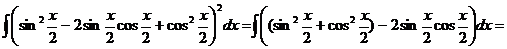
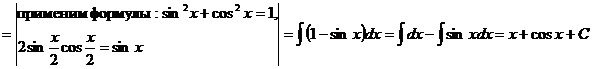 .
. 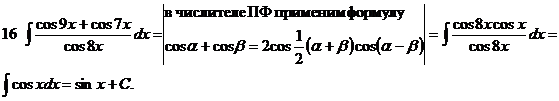
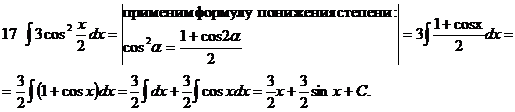
Выполните самостоятельно
18 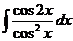 Указание. Примените формулу
Указание. Примените формулу  и выполните почленное деление числителя ПФ на знаменатель.
и выполните почленное деление числителя ПФ на знаменатель.
19  20
20 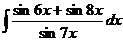 21
21 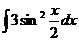
Указание. Примените формулу: 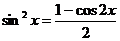 .
.
22  =|примените формулу:
=|примените формулу: 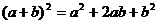 |=
|=  = |примените формулу
= |примените формулу 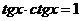 |=
|= 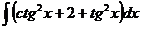 =
=  =| примените формулы
=| примените формулы 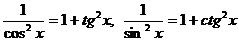 |=
|= 
|
|
|
Интегрирование дробно- рациональных функций с помощью дополнительных преобразований
Замечание. При вычислении неопределенных интегралов непосредственным способом применяются дополнительные или искусственные преобразования, не нарушающие равносильности подынтегральной функции.
Рассмотрим на конкретных примерах
23 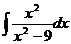

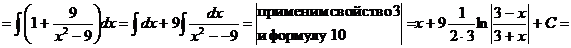
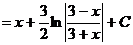 .
.
24 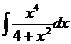
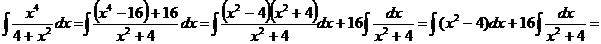
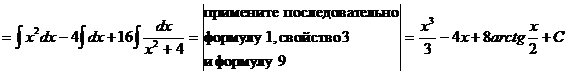 .
.
25  .
.
26 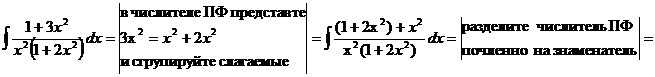
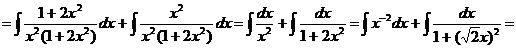
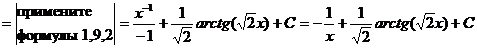
Выполните самостоятельно
27  28
28 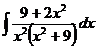 29
29 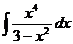 30
30  31
31 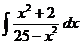
Метод интегрирования подстановкой (замена переменной)
Метод интегрирования подстановкой заключается во введение новой переменной интегрирования (т.е. подстановки). При этом заданный интеграл приводится к новому интегралу, который является табличным или к нему сводится (в случае «удачной» подстановки). Умение правильно определить подстановку приобретается практикой. Тем не менее, рассмотрим несколько общих подходов (назовем их правилами) к данному методу, что позволит систематизировать умение интегрировать методом подстановки и определять новую переменную.
2.2.1 Интегрирование функций (табличные интегралы) к аргументу, которых прибавляется постоянная величина
|
|
|
Рассмотрим некоторые табличные интегралы к аргументу, которых прибавляется (вычитается) постоянная величина 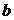 .
.
32 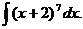
Решение. Введем подстановку x +2 = t (*). Найдем дифференциал от правой и левой частей равенства (*), получим:
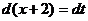 ,
, 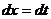 ,
,
Подставим вместо x +2 и 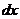 их значения через t в данный интеграл, получим:
их значения через t в данный интеграл, получим:

Легко заметить, что формулы интегрирования сохраняют инвариантность (вид). В данном случаи степенная функция интегрируется по аргументу (х+2).
33 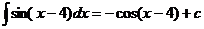
Правило 1
Если к аргументу подынтегральной функции прибавляется (вычитается) постоянная величина 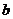 , то формулы интегрирования сохраняют инвариантность , то формулы интегрирования сохраняют инвариантность
|
34 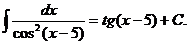
2.2.2 Интегрирование функций (табличные интегралы) аргумент, которых умножается
На постоянную величину
Рассмотрим некоторые табличные интегралы аргумент, которых умножается на постоянную величину 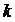
35 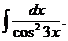
Решение. Введем подстановку 3 x = t (*). Найдем дифференциал от правой и левой частей равенства (*), получим:
|
|
|
 ,
, 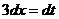 ,
, 
Подставим вместо 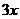 и
и 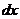 их значения через t в данный интеграл, получим:
их значения через t в данный интеграл, получим:
 | заменим t его выражением через x|=
| заменим t его выражением через x|= 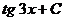
Замечание В дальнейшем процедура решения, представленная, в примерах 32, 35 будет записываться в виде:
 .
.
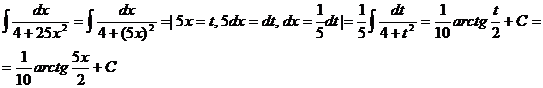
36 
Правило 2
Если аргумент подынтегральной функции умножается на постоянную величину 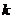 , то формулы интегрирования сохраняют инвариантность, результат интегрирования умножается на число , то формулы интегрирования сохраняют инвариантность, результат интегрирования умножается на число 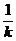 . .
|
37 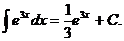
38 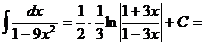

Замечание. Правила 1 и 2 к подынтегральной функции могут применяться одновременно.
39 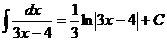 40
40 
41 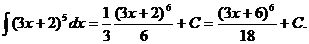
42 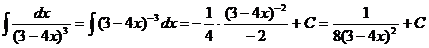
43 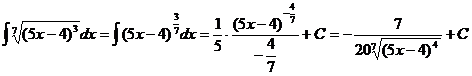
Выполните самостоятельно
44 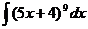 .
.
45 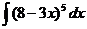
46 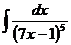 .
.
49 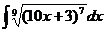 .
.
48 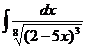
2.4 Интегралы вида: 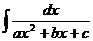 ,
, 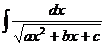
Интегралы данного вида находятся путем выделения полного квадрата из данного
квадратного трехчлена по формуле:
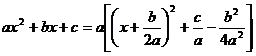 (**) и применения правил 1,2.
(**) и применения правил 1,2.
Интеграл 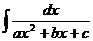 , после выделения полного квадрата сводится к формулам 9 или 10.
, после выделения полного квадрата сводится к формулам 9 или 10.
|
|
|
Интеграл 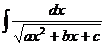 , после выделения полного квадрата сводится к формулам 8 или
, после выделения полного квадрата сводится к формулам 8 или
11.
50 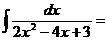 |выделите в знаменатели ПФ полный квадрат по формуле (**)| =
|выделите в знаменатели ПФ полный квадрат по формуле (**)| = 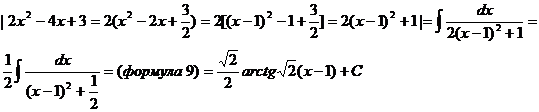
51 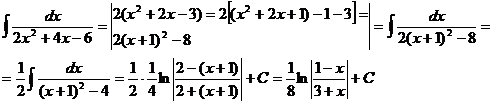
52  = (сомножитель (-1) внесем в квадратные скобки, получим
= (сомножитель (-1) внесем в квадратные скобки, получим 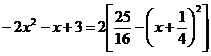 )=
)=
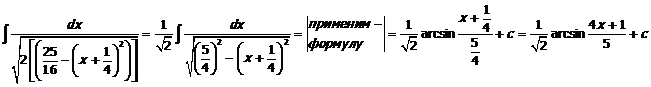
Выполните самостоятельно
53 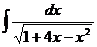 54
54 
55  56
56 
2.2.3 Интегрирование дробных функций (рациональных или иррациональных), когда в знаменатели или под корнем в знаменатели стоит функция, производная которой равна числителю (или приводится к числителю).
Интегралы этого вида находятся путем замены многочлена стоящего в знаменателе ПФ новой переменной
57 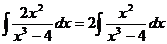
Замечаем, что производная знаменателя ПФ 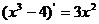 , отличается от числителя только постоянным множителем. Выполним интегрирование, за новую переменную примем
, отличается от числителя только постоянным множителем. Выполним интегрирование, за новую переменную примем 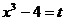
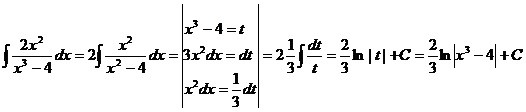
58 
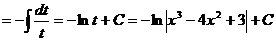
Легко заметить, что если в числителе стоит производная знаменателя, то интеграл всегда равен натуральному логарифму знаменателя.
59 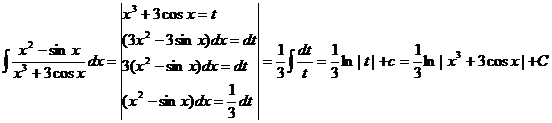
60 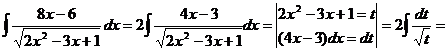
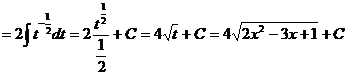
61 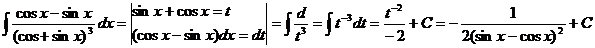
Правило 3
Если под знаком интеграла стоит дробная функция (рациональная или иррациональная), в знаменателе которой или под корнем в знаменателе содержится функция, производная которой равна числителю (или приводится к числителю), то интеграл вычисляется способом замены переменной, причем функция, стоящая в знаменатели обозначается за t .
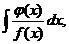 где где 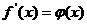 или или  где где 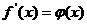 , то , то 
|
Выполните самостоятельно
62 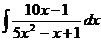 63
63 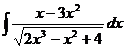
64  65
65 
2.2.4 Интегралы вида: 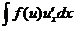
В пункте 2.2.4 рассмотрим интегралы, в которых ПФ представлена как произведение сложной функции и производной ее промежуточного аргумента. В этом случае промежуточный аргумент принимается за новую переменную t .
Например 
Функция  сложная, ее промежуточный аргумент равен
сложная, ее промежуточный аргумент равен 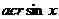 , производная которого
, производная которого 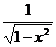 содержится в ПФ, поэтому интеграл сводится к табличной подстановке
содержится в ПФ, поэтому интеграл сводится к табличной подстановке 
Рассмотрим интегралы данного вида
66 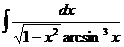
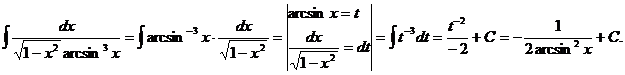
67  =
= 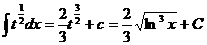
68 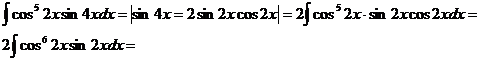
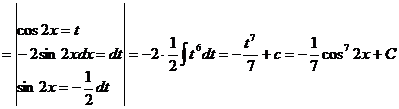
69 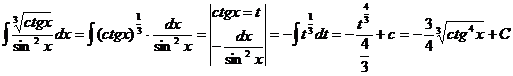
70 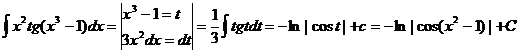
71 
72 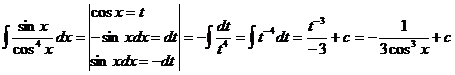
73 
Выполните самостоятельно

74  75
75 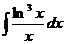
76 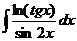 77
77 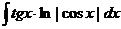
Правило 4
Если под знаком интеграла стоит сложная функция в произведение с производной своего промежуточного аргумента , то интеграл вычисляется способом замены переменной, причем промежуточный аргумент обозначается за t .
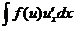 , , 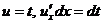
|
Замечание Используя правило 4 вычисляются интегралы, которые с помощью подстановки сводятся к табличным интегралам по формулам 8-11. (Обратите внимание, что данные интегралы имеют «специфический» вид).
78 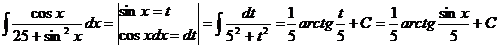
79 
80 
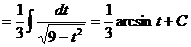
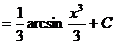
81 
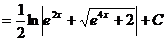
Выполните самостоятельно
82 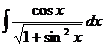 83
83 
84 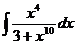 85
85 
Дата добавления: 2021-01-20; просмотров: 74; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
