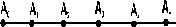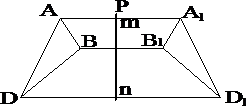Тема 1.2. Способы описания кристаллов

Физико-технологический факультет

Кафедра «Металловедение, порошковая металлургия, наноматериалы»

Конспект лекций по дисциплине

Кристаллография и дефекты кристаллической решетки

Самара 2013

Лекции

Тема 1.1.Строение кристалла.

Теория решётчатого строения кристаллов была создана в середине 19 века французским кристаллографом О. Бравэ, а затем русский кристаллограф академик Е. С. Фёдоров и немецкий учёный А. Шенфлис завершили математическую разработку этой теории. При создании и разработке теории решетчатого строения кристаллов Бравэ, Фёдоров и др. кристаллографы основывались исключительно на некоторых важных свойствах кристаллического вещества.

Основными свойствами кристаллов являются их однородность, анизотропность, способность самоограняться и симметричность.

Однородным обычно называют тело, которое обнаруживает одинаковые свойства во всех своих частях. Кристаллическое тело однородно, т. к. различные участки его имеют одинаковое строение, т. е. одинаковую ориентировку слагающих частиц, принадлежащих одной и той же пространственной решётке. Однородность кристалла следует отличать от однородности жидкости или газа, которая имеет статистический характер.

Анизотропным называется такое однородное тело, которое обладает неодинаковыми свойствами по непараллельным направлениям. Кристаллическое тело анизотропно, т. к. строение пространственной решётки, а значит и самого кристалла, в общем случае неодинаково по непараллельным направлениям. По параллельным же направлениям частицы слагающие кристалл, как и узлы его пространственной решётки, расположены строго одинаковым образом, поэтому и свойства кристалла по таким направлениям должны быть одними и теми же.

Характерный пример резко выраженной анизотропности представляет слюда, кристаллы которой легко расщепляются лишь по одному определённому направлению. В качестве другого яркого примера анизотропности можно привести минерал дистен (AlOAl[SiO₄]), у кристаллов которого боковые грани имеют сильно различающиеся значения твердости в продольном и поперечном направлениях. Если из кристалла каменной соли, имеющего форму куба, вырезать стерженьки по разным направлениям, то для разрыва этих стерженьков потребуются разные усилия. Стерженёк, перпендикулярный граням куба, разорвётся при усилии около 570 Г/мм²; для стерженька, параллельного гранным диагоналям, разрывающее усилие составит 1150 Г/мм², а разрыв стерженька, параллельного телесной диагонали куба, произойдет при усилии 2150 Г/мм².

Правильная геометрическая форма кристаллов с давних пор привлекала внимание человека, и её загадочность вызывала в прошлом у людей различные суеверия. Кристаллы таких веществ, как алмаз, изумруд, рубин, сапфир, аметист, топаз, бирюза, гранат и др., ещё в 18 в. считались носителями сверхъестественных сил и использовались не только как драгоценные украшения, но и как талисманы или средство от многих болезней и укусов ядовитых змей.

На самом же деле способность самоограняться, как и первые два свойства, является следствием правильного внутреннего строения кристаллического вещества. Внешние границы кристаллов как бы отражают эту правильность их внутреннего строения, ибо каждый кристалл можно рассматривать как часть его пространственной решётки, ограниченной плоскостями (гранями).

Необходимо вместе с тем отметить, что способность кристаллического вещества самоограняться проявляется не всегда, а только при особо-благоприятных условиях, когда внешняя окружающая среда не мешает образованию и свободному росту кристаллов. При отсутствии таких условий получаются или совершенно неправильные или частично деформированные кристаллы. Несмотря на это они сохраняют все свои внутренние свойства, в том числе и причины, заставляющие кристаллы принимать форму многогранника. Поэтому, если кристаллическое зерно неправильной формы поместить в определённые условия, в которых кристалл сможет свободно расти, то оно примет через некоторое время форму плоскостного многогранника, присущую данному веществу.

Симметрия кристаллов также является отражением их закономерного внутреннего строения. Все кристаллы в той или иной степени симметричны, т. е. состоят из закономерно повторяющихся равных частей, так как их строение выражается пространственной решёткой, которая по своей природе всегда симметрична.

Познакомимся теперь подробнее с построением и некоторыми свойствами пространственной решётки.

Примем какой-либо узел пространственной решётки, например, узел А₀, за исходный узел решётки (рис. 1.1). Пусть ближайший к нему такой же атом (узел) А₁ находится на расстоянии а (а --> А₀А₁). Продолжив прямую А₀А₁, найдем серию узлов А₂,А₃, А₄, . . . , А_n, расположенных вдоль этой прямой на равном расстоянии друг от друга.

Совокупность узлов, лежащих на одной прямой, называется рядом пространственной решётки.

Рис. 1.1. Ряд пространственной решётки

Расстояние между соседними узлами ряда называется промежутком ряда. В нашем случае промежуток ряда равен а.

Число узлов, приходящихся на единицу длины ряда, называется плотностью ряда. Очевидно, что плотность ряда обратно пропорциональна величине промежутка: чем меньше промежуток ряда, тем больше будет его плотность.

Одно из основных свойств пространственной решётки состоит в том, что через любой узел решётки всегда можно провести ряд, параллельный данному ряду, причём все параллельные ряды имеют одинаковую плотность. Ряды же разных направлений в общем случае обладают различной плотностью. В частных случаях и у непараллельных рядов промежутки могут быть одинаковыми.

Возьмём теперь относительно исходного узла А₀ ещё один ближний к нему узел, лежащий в плоскости чертежа, но не вне ряда А₀А_n. Пусть это будет узел В₁, отстоящий от узла А₀ на расстояние b (рис. 1.2). Соединив узлы А₀ и В₁ прямой линией и продолжив её дальше, получим новый ряд А₀В_nс промежутком ряда b.

Два пересекающихся ряда А₀А_n и А₀В_n, определяют положение плоскости, которая пройдёт через бесконечное множество узлов пространственной решётки.

Совокупность узлов пространственной решётки, лежащих в одной плоскости, называется плоской сеткой.

Узлы всякой плоской сетки можно расположить в вершинах равных и параллельных друг другу параллелограммов, смежных по целым сторонам. Такую систему параллелограммов в нашем случае получим, если через узлы В₁, В₂, . . . , В_n проведём ряды, параллельные ряду А₀А_n, а через узлы А_2.,А_3,А_4, . . . ,А_n, - ряды, параллельные ряду А₀В_n (см. рис. 2) .

Рис. 1.2. Плоская сетка Рис.1. 3. Пространственная решётка

Три серии построенных плоских сеток, взаимно пересекаясь, образуют систему равных, параллельно ориентированных и смежных по целым граням параллелепипедов, т. е. пространственную решётку. На рис.1.3 один из параллелепипедов решётки выделен жирными линиями. Все узлы полученной решётки располагаются только в вершинах параллелепипедов. Если известно расположение узлов решётки у одного параллелепипеда, то можно построить всю решётку параллельным повторением данного, поступательно перемещая параллелепипед на величину его рёбер по их направлению.

Параллелепипед, поступательным перемещением которого на величину и по направлению его рёбер можно построить всю пространственную решётку, называется параллелепипедом повторяемости или элементарной ячейкой

Параллелепипеды повторяемости можно выделить у данной пространственной решётки самым различным образом (рис. 1.4).

Рис. 1.4. Различные параллелепипеды повторяемости пространственной решётки

Если узлы решётки располагаются только в вершинах параллелепипедов повторяемости, то каждый узел принадлежит одновременно восьми попарно смежным параллелепипедам (рис. 1.3). Следовательно, на долю одного параллелепипеда приходится 1/8 узла, находящегося в его вершине. Поэтому на один примитивный параллелепипед приходится всего 1/8 × 8 = 1 узел пространственной решётки.

Одна и та же пространственная решётка может быть разбита на примитивные параллелепипеды различными способами, но каким бы способом мы ни разбивали нашу решётку на параллелепипеды, её общий объём и количество узлов остаются неизменными. А так как каждому узлу отвечает всегда один примитивный параллелепипед, то любые примитивные параллелепипеды данной пространственной решётки имеют одинаковый объём. У всех других параллелепипедов повторяемости, не являющихся примитивными, объём будет больше, так как количество узлов, приходящихся на непримитивный параллелепипед, всегда превышает 1.

Построенная нами пространственная решётка представляет собой бесконечную фигуру, поскольку каждый из рядов решётки может быть продолжен неопределённо далеко.

Кристаллическая решетка строится по принципу трансляции (сдвига) элементарной ячейки без её поворота. Наименьшее расстояние при перемещении на которое вдоль оси трансляции фигура самосовмещается, называется периодом трансляции.

Элементарная ячейка выбирается по правилам: она должна отражать симметрию кристалла, иметь (по возможности) прямые углы и равные стороны и иметь минимально возможный объём.

Лекции

Тема 1.2. Способы описания кристаллов

В решётке параллельно каждой плоской сетке проходит бесконечное множество тождественных плоских сеток. Совокупность параллельных друг другу плоских сеток пространственной решётки будем называть серией плоских сеток. Расстояние между двумя ближайшими параллельными плоскими сетками называется межплоскостным расстоянием.

Считается, что атомы кристалла лежат на некоторых кристаллографических плоскостях . Такими плоскостями являются грани кристалла.

Важнейшим законом кристаллографии, из которого вытекает всё учение о кристаллографических символах, применяемых для определения относительного расположения граней и рёбер кристаллов, является закон рациональных отношений..Закон этот был впервые сформулирован французским кристаллографом Аюи (1723-1826) и поэтому его часто называют “законом Аюи”. Сущность закона Аюи состоит в следующем.

Выберем в кристалле три непараллельных ребра, пересекающихся в одной точке (рис.2 1.). Пусть две непараллельные грани пересекают все три ребра первая грань в точках А₁,В₁,С₁, а вторая в точках А₂,В₂,С₂.

Таким образом грань А₁В₁С₁ отсекает на ребрах О₁,О₂,О₃ отрезки ОА₁, ОВ₁ и ОС₁, а грань А₂В₂С₂ - отрезки ОА₂, ОВ₂ и ОС₂.

Разделим отрезки отсекаемые на рёбрах одной гранью, на соответственные отрезки другой грани, а затем возьмём отношение трёх полученных дробей. В результате получим двойные отношения отрезков, которые можно заменить отношениями:

ОА₂/ ОА₁: ОB₂/ ОB₁: ОC₂/ ОC₁=m:n:p

где m,n,p- целые взаимно простые числа.

Это математическое выражение закона рациональности: “Двойные отношения отрезков, отсекаемых двумя любыми гранями кристалла на трёх пересекающихся рёбрах его, равны отношениям целых и сравнительно небольших взаимно простых чисел”.

Рис. 2.1. Грани А₁В₁С₁ и А₂В₂С₂ отсекают на ребрах О1, О2, О3 отрезки, отношения которых равны отношениям простых чисел

Закон Аюи объясняется решётчатым строением кристаллов. Грани на рис. 2.1 соответствуют плоским сеткам, а рёбра рядам решётки.

Положение граней кристаллов определяется относительно некоторой системы координат, выбираемой так, чтобы координатные оси были параллельны рядам пространственной решётки.

Направления в кристалле, параллельные рядам его пространственной решётки принятые за оси координат, называют кристаллографическими осями.

Отрезки, отсекаемые гранью кристалла на кристаллографических осях, называют параметрами этой грани.

Грань, линейные размеры которой по всем кристаллографическим осям приняты за единицы измерения параметров остальных граней кристаллов, называется единичной гранью.

В общем случае каждая грань имеет свой масштаб.

На рис. 2.2 грань А₀В₀С₀ принята в качестве единичной грани. Найдём число единичных отрезков

ОА_x/ ОА₀=р; ОB_x/ ОB₀=q; ОC_x/ ОC₀=r, где

числа p,q,r – числовые параметры грани.

Если взять обратное отношение имеем:

ОА₀/ ОА_x: ОB₀/ ОB_x: C₀/ОC_x= = h:k:l

где h,k,l-целые взаимно простые числа.

Рис.2.2. Символ грани А_хВ_хС_х определяется из двойных отношений

Эти числа называются индексами грани и служат характеристикой её положения в кристаллографической системе координат.

Индексами грани кристалла (индексами плоскости) называются целые взаимно простые числа, обратно пропорциональные числовым параметрам этой грани.

Совокупность индексов данной грани, взятых в круглые скобки образует символ грани (плоскости).

Положение любой плоскости в пространстве определяется тремя точками. Ими служат точки пересечения выбранной плоскости с осями координат. Для ориентации кристаллографических плоскостей проводят оси, совпадающие с ребрами элементарной ячейки, а за начало координат этих осей выбирают один из узлов кристаллической решетки, в котором пересекаются эти ребра. Такие оси называют кристаллографическими, а длины ребер элементарной ячейки — осевыми единицами. Масштаб по осям х, у, z в общем случае может быть различным.

Пусть кристаллографические оси х, у, z пересекаются плоскостью Р. Эта плоскость отсекает на оси х отрезок а, на оси у отрезок b и на оси z отрезок с. Ориентация плоскости задается величинами, обратными длинам отсекаемых отрезов которые называют индексами Миллера. Для нахождения индексов обратные величины l/a , 1/b , 1/c приводят к общему знаменателю, затем знаменатель отбрасывают. Полученные числа h, k, l и есть индексы Миллера для указанной плоскости.

Примеры плоскостей в кристалле

1. Символ (111) всегда отвечает единичной грани.

Символ единичной грани - (111) ,хотя, как уже указывалось выше, единичные отрезки на кристаллографических осях могут быть не равны друг другу.

2. В символе грани, параллельной какой-либо кристаллографической оси, индекс, соответствующий этой оси равен нулю.

3. Грань, пересекающая одну кристаллографическую ось и параллельная двум другим, имеет символ, один индекс которого равен единице, а два других - нулю.

С помощью индексов Миллера можно описать и направления в кристалле. Поскольку любое направление можно изобразить линией, проходящей через начало координат, то с помощью координат первого узла, лежащего на этой прямой, можно определить миллеровские индексы направления, Их находят так же, как индексы плоскости. Индексы направления обозначают буквами и, v, w и заключают в квадратные скобки: [и v w].

Например, [100] — направление оси х, [111] — диагональ рассматриваемого куба. Для кубической системы направление [и v w] перпендикулярно плоскости (hkl), если и = h, v = k, w = l.

Лекции

Тема 2.1 Элементы симметрии

Симметрия - широко распространенное в природе явление. Особенно многообразно симметрия проявляется в мире животных и растений. Кристаллы - наиболее яркие представители симметричных тел неживой природы.

Всякая симметричная фигура состоит из закономерно повторяющихся равных частей.

Операция совмещения частей симметричной фигуры и фигуры в целом называется симметрическим преобразованием.. Каждому элементу отвечает своё симметрическое преобразование, посредством которого фигура совмещается сама с собой.

В кристаллических многогранниках возможны элементы симметрии: плоскости симметрии, центр инверсии, оси симметрии и инверсионные оси.

Плоскостью симметрии называется плоскость, которая делит фигуру на две равные части, расположенные друг относительно друга как предмет и его зеркальное отражение. Плоскость симметрии обозначается буквой Р.

Рис 3.1. Плоскость симметрии

Симметрическое преобразование, отвечающее плоскости симметрии, есть отражение в плоскости. При нахождении плоскостей симметрии мысленно рассекают их плоскостью на две половины так, чтобы при отражении в этой плоскости половинки совместились друг с другом

Кристаллические многогранники могут иметь одну или несколько плоскостей симметрии. Число плоскостей симметрии указывается коэффициентом, стоящим перед буквой Р. Например, куб имеет 9Р, т. е. девять плоскостей симметрии.

Рис. 3.2 Куб имеет девять плоскостей симметрии (9Р):

три главных плоскости (а) и шесть диагональных (б)

Следует помнить, что плоскости симметрии или перпендикулярны к рёбрам и граням многогранника и проходят через их середины, или проходят вдоль рёбер.

Центр инверсии называют центром обратного равенства, потому что каждая грань при наличие центра инверсии должна иметь равную себе и обратно параллельную грань

Осью симметрии называется прямая линия, при повороте вокруг которой на некоторый определённый угол фигура совмещается сама с собой.

Рис. 3.3 Многогранники с центром инверсии и без центра

Наименьший угол поворота, приводящий фигуру к самосовмещению, называется элементарным углом поворота оси. Элементарный угол поворота оси a содержится целое число раз в 360^°:

360/a = n

где n – целое число.

Число n, показывающее сколько раз элементарный угол поворота оси содержится в 360⁰, называется порядком оси.

В геометрических фигурах могут присутствовать оси любых порядков, начиная от оси первого порядка и кончая осью бесконечного порядка.

Элементарный угол поворота оси первого порядка (n = 1) равен 360⁰. Так как каждая фигура, будучи повернута вокруг любого направления на 360⁰, совмещается сама с собой, то всякая фигура обладает бесконечным количеством осей первого порядка. Такие оси не являются характерными, поэтому они обычно не упоминаются.

Ось бесконечного порядка отвечает бесконечно малому элементарному углу поворота. Эта ось присутствует во всех фигурах вращения в качестве оси вращения.

В кристаллических же многогранниках возможны не любые оси симметрии, а только оси первого, второго, третьего, четвертого и шестого порядка.

Оси симметрии пятого и выше шестого порядка в кристаллах невозможны. Это положение является одним из основных законов кристаллографии и называется законом симметрии кристаллов.

Для обозначения осей симметрии употребляется буква L, а порядок оси указывается маленькой цифрой, располагаемой справа от буквы (например, L₄ - ось четвертого порядка).

В кристаллических многогранниках оси симметрии могут проходить через центры противоположных граней перпендикулярно к ним, через середины противоположных ребер перпендикулярно к ним (только L₂) и через вершины многогранника. В последнем случае симметричные грани и ребра одинаково наклонены к данной оси.

Кристалл может иметь несколько осей симметрии одного порядка, количества которых указывается коэффициентом перед буквой. Например, в прямоугольном параллелепипеде присутствует 3L₂, т. е. три оси симметрии второго порядка; в кубе имеются 3L₄, 4L₃ и 6L₂, т. е. три оси симметрии четвертого порядка, четыре оси третьего порядка и шесть осей второго порядка и т. д.

Инверсионной осью симметрии называется прямая линия, при повороте вокруг которой на некоторый определенный угол с последующим отражением в центральной точке фигуры, как в центре инверсии, фигура совмещается сама с собой.

Симметричное преобразование, отвечающее инверсионной оси, состоит из поворота вокруг прямой линии и последующей инверсии в точке, лежащей на этой линии.

Рассмотрим пример инверсионной оси в правильной треугольной призме на рис. В этой фигуре прямая gg является осью симметрии третьего порядка L₃ и одновременно инверсионной осью шестого порядка. Действительно после поворота вокруг этой оси на 60° всех частей многогранника и последующего их отражения в центральной точке фигура самосовмещается.

Рис. 3.4. Ось инверсии шестого порядка

В кристаллических многогранниках возможны инверсионные оси первого, второго, третьего, четвертого и шестого порядка, т.е. L_i1, L_i2, L_i3, L_i4, L_i6.

На практике приходится иметь дело в основном с двумя последними инверсионными осями L_i4 и L_i6. Остальные инверсионные оси могут быть заменены другими, уже знакомыми нам элементами симметрии.

Так, например, инверсионная ось первого порядка (L_i1) равнозначна центру инверсии (C). Действительно поворот на 360° оставляет фигуру на месте, поэтому самосовмещение фигуры произойдет только в результате отражения в центральной точке. Следовательно, L_i1=С.

Инверсионная ось второго порядка по своему действию равнозначна перпендикулярной к ней плоскости симметрии, т. е. L_i2=Р.

Инверсионная ось третьего порядка L_i3 равносильна одновременно действующим оси симметрии третьего порядка L₃, совпадающей с L_i3и центру инверсии С, т. е. , L_i3=L₃С. Так, например, в кубе, где присутствует совместно С и L₃, каждая из четырех осей симметрии третьего порядка является в то же время тройной инверсионной осью. Наличие L_i3, всегда совпадающей с простой осью симметрии третьего порядка, обычно не указывается.

Инверсионная ось четвертого порядка L_i4 является самостоятельным элементом симметрии и не может быть ничем заменена. В многогранниках, обладающих L_i4, центр инверсии отсутствует. Четвертая инверсионная ось всегда является одновременно осью симметрии второго порядка (L_i4=L₂), однако не любая двойная ось при отсутствии С отвечает L_i4.

Инверсионная ось шестого порядка L_i6 может быть заменена осью симметрии третьего порядка, совпадающей с L_i6 и перпендикулярной к ней плоскостью симметрии:

L_i₆=L₃P(P ^ L₃)

Кристаллические многогранники, обладающие L_i6, самостоятельного центра инверсии не имеют.

Лекции

Дата добавления: 2021-01-20; просмотров: 101; Мы поможем в написании вашей работы!

Поделиться с друзьями:

12 3 4 Следующая ⇒

Мы поможем в написании ваших работ!