Главная часть бесконечно-малой.
Определение. Если 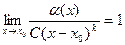 то функция
то функция  называется ГЛАВНОЙ ЧАСТЬЮ бесконечно-малой
называется ГЛАВНОЙ ЧАСТЬЮ бесконечно-малой  .
.
Фактически, это степенная функция, эквивалентная данной  . Если найти коэффициент
. Если найти коэффициент  и степень
и степень  , то мы найдём такую степенную функцию, график которой наилучшим образом (среди всех степенных) похож на график функции
, то мы найдём такую степенную функцию, график которой наилучшим образом (среди всех степенных) похож на график функции  в окрестности точки.
в окрестности точки.
Задача 211. Найти главную часть бесконечно-малой 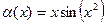 в точке 0.
в точке 0.
Решение. Так как точка 0, то 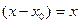 , то есть главная часть имеет вид
, то есть главная часть имеет вид  . Запишем отношение данной бесконечно-малой и «эталонной» степенной. Нужно потребовать, чтобы этот предел был 1, ведь мы ищем именно эквивалентную бесконечно-малую.
. Запишем отношение данной бесконечно-малой и «эталонной» степенной. Нужно потребовать, чтобы этот предел был 1, ведь мы ищем именно эквивалентную бесконечно-малую.
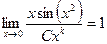 . Преобразуем выражение с целью его упростить. Домножим и поделим на
. Преобразуем выражение с целью его упростить. Домножим и поделим на 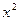 , этим мы фактически можем заменить
, этим мы фактически можем заменить 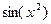 на
на 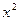 . Параметры C и k пока просто переписываем, не меняя их в процессе преобразований.
. Параметры C и k пока просто переписываем, не меняя их в процессе преобразований.
 =
= 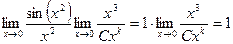 .
.
Полное сокращение всех 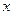 будет лишь в случае k=3, а иначе предел 0 или
будет лишь в случае k=3, а иначе предел 0 или  , и не будет равен 1.
, и не будет равен 1.
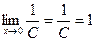 , тогда С = 1. Итак,
, тогда С = 1. Итак,  =
=  .
.
Ответ.  .
.

Изображены графики бесконечно-малой и её главной части:
как видно, вблизи (0,0) они практически неотличимы.
Задачи на поиск главной части по методам и сложности похожи на вычисление lim, но фактически это обратная задача: при вычислении предела внутри нет параметров, а предел неизвестен, здесь же наоборот, известно, что предел равен 1, но внутри выражения неизвестные параметры C, k, которые надо найти, так, чтобы предел был равен 1.
Непрерывность и точки разрыва.
Определение. 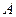 называется правосторонним пределом функции
называется правосторонним пределом функции 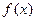 в точке
в точке  , если:
, если: 
 , так, что при
, так, что при 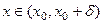 выполняется:
выполняется:  .
.
Обозначается  .
.
Аналогично, 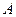 называется левосторонним пределом функции
называется левосторонним пределом функции  в точке
в точке  , если:
, если: 
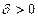 , так, что при
, так, что при 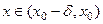 выполняется:
выполняется:  .
.
Обозначается  .
.
Определение. Функция называется непрерывной в точке 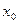 , если в этой точке определено значение
, если в этой точке определено значение 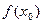 , и оно совпадает как с правосторонним так и с левосторонним пределами:
, и оно совпадает как с правосторонним так и с левосторонним пределами:
 .
.
Если это не выполняется, точка называется точкой разрыва.
Типы точек разрыва.
| Название | Устранимый | Разрыв 1 рода | Разрыв 2 рода |
| Определение | 

| 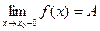
 , , 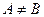 . .
| Один или оба 1-ст lim равны 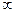 или не сущ. или не сущ.
|
| Примеры | 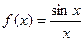
| 

| 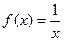
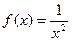
|
Примеры  точка разрыва
точка разрыва 
 точки разрыва 2 и 3.
точки разрыва 2 и 3.
 . Предел слева равен 0, справа
. Предел слева равен 0, справа  . График:
. График:
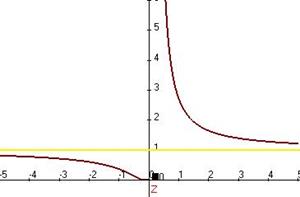
Задача 212. Найти точку разрыва и охарактеризовать её тип:  .
.
Решение. Здесь при любом  верно
верно 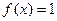 , а при любом
, а при любом 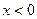 верно
верно 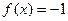 . В точке 0 односторонние пределы различны.
. В точке 0 односторонние пределы различны.

Ответ. Разрыв 1 рода
Задача 213. Охарактеризовать тип точки 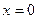 , если
, если  .
.
Решение. Односторонние пределы для этой функции таковы:
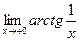 =
=  =
= 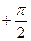 , т.к. если
, т.к. если  и при этом
и при этом  то
то 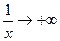 .
.
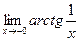 =
= 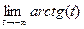 =
= 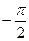 , т.к. если
, т.к. если  и при этом
и при этом 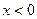 то
то 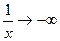 .
.
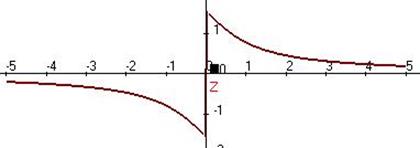
Ответ. Разрыв 1 рода.
Задача 214. Исследовать тип разрыва 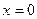 для
для  .
.
Решение. И при  , и при
, и при  здесь
здесь  , а тогда
, а тогда  . Тогда для обоих односторонних пределов получается одинаково:
. Тогда для обоих односторонних пределов получается одинаково:  . Тогда разрыв устранимый.
. Тогда разрыв устранимый.
К тому же функция чётная, и так ясно, что с двух сторон симметричные ветви графика. Так что достаточно было вычислить только с одной стороны. Ответ. 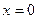 устранимый разрыв.
устранимый разрыв.
Примечание. График этой функции:
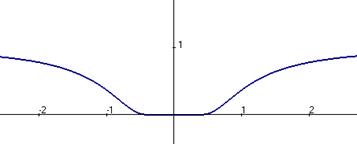
Задача 215. Найти точки разрыва и определить их тип 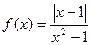 .
.
Решение. Вычислить значение функции обычным путём здесь нельзя лишь в точках 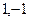 где знаменатель обращается в 0. Эти две точки подозрительные на существование разрыва, мы и будем исследовать.
где знаменатель обращается в 0. Эти две точки подозрительные на существование разрыва, мы и будем исследовать.
Во-первых, можно представить так:  .
.
Надо найти оба односторонних предела в каждой из точек.
Рассмотрим  .
.
Для предела справа,  и модуль раскрывается без лишнего знака:
и модуль раскрывается без лишнего знака:
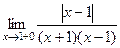 =
= 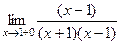 =
= 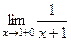 =
= 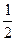 .
.
Для предела слева,  , и при раскрытии модуля знак минус:
, и при раскрытии модуля знак минус:
 =
=  =
=  =
=  .
.
Получились разные константы. Значит, разрыв 1-го рода.
Рассмотрим  .
.
Здесь  и
и 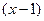 раскрываются одинаково, и равны 2 и
раскрываются одинаково, и равны 2 и  . А отличие в том, какого знака бесконечно-малая
. А отличие в том, какого знака бесконечно-малая 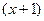 в знаменателе.
в знаменателе.
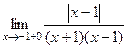 =
= 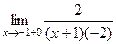 =
=  =
= 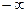 .
.
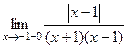 =
= 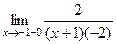 =
=  =
= 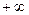 .
.
Хотя бы с одной стороны предел 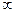 или не существует, значит разрыв 2-го рода.
или не существует, значит разрыв 2-го рода.
Ответ.  разыв 2 рода,
разыв 2 рода,  разрыв 1 рода.
разрыв 1 рода.

Чертёж к этой задаче. Синим цветом показан график этой функции, жёлтым - вертикальная асимптота, где разрыв 2-го рода.
Задача 216. Исследовать тип точки разрыва  для
для  .
.
Решение. Ищем односторонние пределы вокруг 0, но при этом каждый раз домножаем и делим на 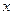 , так чтобы избавиться от синуса в выражении.
, так чтобы избавиться от синуса в выражении.
 =
=  =
=  =
=  = 1.
= 1.
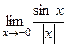 =
= 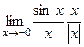 =
=  =
=  =
= 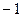 .
.
Здесь знак модуля раскрывается по-разному в зависимости от того, справа или слева от 0 мы находимся. Это либо  либо
либо 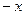 . Получились различные числа. Разрыв 1-го рода.
. Получились различные числа. Разрыв 1-го рода.
Ответ. 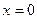 разрыв 1 рода.
разрыв 1 рода.
Примечание. Вот график этой функции:

Задача 217. Выяснить тип точки  для
для 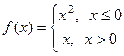 .
.
Решение. Левосторонний предел здесь должен вычисляться с помощью первой ветви функции, а правосторонний с помощью второй. 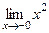 = 0.
= 0. 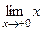 = 0. Кроме того,
= 0. Кроме того, 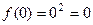 .
.
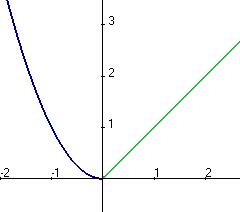
Значение функции существует и равно как левостороннему пределу, так и правостороннему. 0 это точка непрерывности.
Ответ.  точка непрерывности.
точка непрерывности.
График этой функции:
Задача 218. Найти точки разрыва и определить их тип для функции: 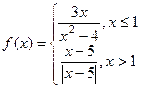 .
.
Решение. Сначала ищем точки, подозрительные на разрыв, то есть где возможен разрыв. Во-первых, это точка стыковки двух ветвей графика, то есть  . Там надо предел слева искать с помощью одной функции, а справа - с помощью другой. Кроме того,
. Там надо предел слева искать с помощью одной функции, а справа - с помощью другой. Кроме того, 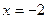 и
и 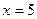 . Точка
. Точка 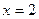 не должна рассматриваться, т.к. правее 1 уже действует другая ветвь функции.
не должна рассматриваться, т.к. правее 1 уже действует другая ветвь функции.
Рассмотрим 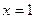 :
:
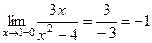 ,
, 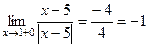 . Кроме того, значение в точке 1 тоже существует и равно
. Кроме того, значение в точке 1 тоже существует и равно  .
.
Тогда  точка непрерывности.
точка непрерывности.
Рассмотрим 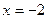 :
:
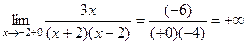 .
.  .
.  разрыв 2-го рода.
разрыв 2-го рода.
Рассмотрим  .
.

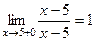 ,
, 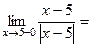
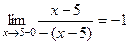 .
.
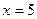 разрыв 1-го рода.
разрыв 1-го рода.
Ответ. 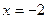 разрыв 2 рода,
разрыв 2 рода,  точка непрерывности,
точка непрерывности,
 разрыв 1 рода.
разрыв 1 рода.
На графике синим цветом показана левая ветвь функции, зелёным - правая, жёлтым - асимптота (она там, где разрыв 2 рода). График этой функции:
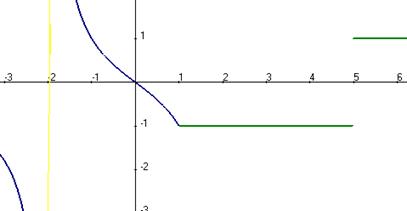
Асимптоты.
Если  то
то 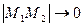 .
.
Горизонтальные: Если 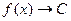 ,
, 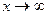 , то асимптота горизонтальная, эта ситуация имеет место, когда
, то асимптота горизонтальная, эта ситуация имеет место, когда  .
.

Пример.  две односторонние горизонтальные асимптоты:
две односторонние горизонтальные асимптоты: 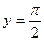 и
и 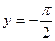 .
.

Вертикальные: Если 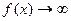 ,
,  , то асимптота вертикальная (это соответствует разрыву 2 рода,
, то асимптота вертикальная (это соответствует разрыву 2 рода,  ).
).
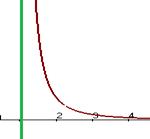
Наклонные асимптоты.
Задача 219. Вывод формул  и
и 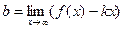 .
.
Так как точка на графике и на асимптоте сближаются то:
 .
.
Отсюда следует, что 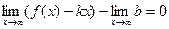 , то есть
, то есть
 .
.
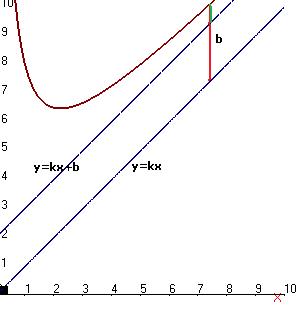
Рассмотрим прямую 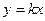 , параллельную асимптоте
, параллельную асимптоте 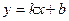 .
.
Если разность ординат для точки на графике и соответствующей точки на прямой  стремится к 0, то разность ординат для точки на графике и точки на прямой
стремится к 0, то разность ординат для точки на графике и точки на прямой 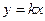 стремится к
стремится к  . Отрезок, соответствующий этому расстоянию, отмечен красным на чертеже.
. Отрезок, соответствующий этому расстоянию, отмечен красным на чертеже.
Если две величины, 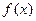 и
и  , неограниченно возрастают, и при этом разность между ними стремится к 0, то их отношение стремится к 1, то есть
, неограниченно возрастают, и при этом разность между ними стремится к 0, то их отношение стремится к 1, то есть  . Но ведь также очевидно, что
. Но ведь также очевидно, что 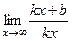 =
=  = 1.
= 1.
Тогда рассмотрим  , этот предел равен 1. Однако если сократить в нём
, этот предел равен 1. Однако если сократить в нём 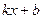 то
то 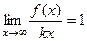 , а тогда
, а тогда 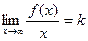 .
.
Итак, мы получили формулы для нахождения  . На практике сначала надо найти
. На практике сначала надо найти  , а уже затем
, а уже затем  .
.
Пример 220. Найти асимптоты графика функции 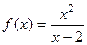 .
.
Решение. Во-первых, сразу видно точку разрыва 2-го рода 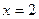 . Есть вертикальная асимптота
. Есть вертикальная асимптота  .
.
Найдём наклонную асимптоту.
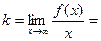
 (мы просто добавили лишний
(мы просто добавили лишний  в знаменателе, тем самым поделили на
в знаменателе, тем самым поделили на  ).
).
 =
= 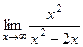 =
= 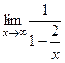 = 1. Итак,
= 1. Итак,  .
.
Обратите внимание: здесь предел одинаково вычисляется при 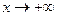 и при
и при 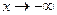 , но бывают примеры, в которых по-разному, то есть на правой и левой полуплоскости могут быть разные асимптоты.
, но бывают примеры, в которых по-разному, то есть на правой и левой полуплоскости могут быть разные асимптоты.
Найдём  =
=  =
=  =
= 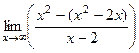 =
=  =
= 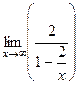 = 2.
= 2.
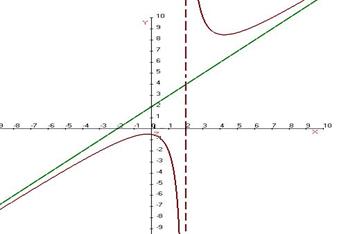
Ответ. Вертикальная x = 2, наклонная y = x + 2.
График выглядит так:
Задача 221. Найти асимптоты графика функции 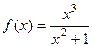 .
.
Решение. Во-первых, знаменатель не обращается в 0, поэтому точек разрыва 2-го рода нет, и нет вертикальных асимптот. Горизонтальных асимптот также нет, т.к. 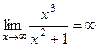 , предел не константа С.
, предел не константа С.
Ищем наклонные асимптоты.
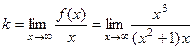 =
= 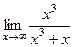 = 1.
= 1.
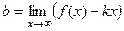 =
= 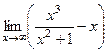 =
= 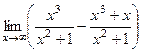 =
=
 . Асимптота
. Асимптота  . Чертёж:
. Чертёж:
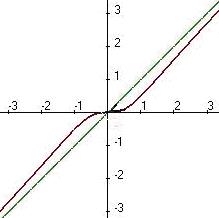
Ответ. Асимптота  .
.
Задача 222. Найти асимптоты графика функции  .
.
Решение. Во-первых, при 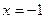 знаменталь обращается в 0, здесь разрыв 2 рода. То есть, вертикальная прямая
знаменталь обращается в 0, здесь разрыв 2 рода. То есть, вертикальная прямая  это вертикальная асимптота. Теперь ищем наклонные асимптоты.
это вертикальная асимптота. Теперь ищем наклонные асимптоты.
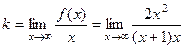 =
=  = 2. Причём этот результат не зависит от того, предел при
= 2. Причём этот результат не зависит от того, предел при  или
или 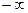 , ведь обе старшие степени чётные. Нашли
, ведь обе старшие степени чётные. Нашли  , т.е. есть наклонная асимптота типа
, т.е. есть наклонная асимптота типа 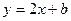 . теперь найдём
. теперь найдём 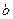 .
.
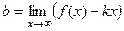 =
= 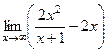 =
=  =
=
 =
=  =
=  . Итак,
. Итак, 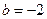 и опять же, это независимо от
и опять же, это независимо от 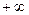 или
или 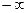 . Значит, прямая
. Значит, прямая 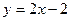 это двусторонняя асимптота.
это двусторонняя асимптота.
Ответ. Вертикальная  и наклонная
и наклонная 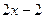 . График:
. График:
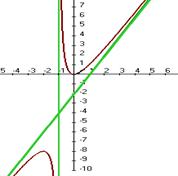
Задача 223. Найти асимптоты графика функции  .
.
Решение. Область определения: 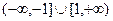 . Здесь нет знаменателя, который мог бы обращаться в 0, поэтому вертикальных асимптот нет. Функция не ограниченная при
. Здесь нет знаменателя, который мог бы обращаться в 0, поэтому вертикальных асимптот нет. Функция не ограниченная при  , поэтому и горизонтальных асимптот нет, так что ищем только наклонные. Функция чётная, поэтому можем искать только при
, поэтому и горизонтальных асимптот нет, так что ищем только наклонные. Функция чётная, поэтому можем искать только при 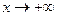 на правой полуплоскости, а на левой график симметричен, так что если
на правой полуплоскости, а на левой график симметричен, так что если  будет асимптотой на правой полуплоскости, то
будет асимптотой на правой полуплоскости, то
 на левой. А вот двусторонняя асимптота здесь никак не могла бы быть, ведь график симметричен относительно вертикальной оси, т.к. функция чётная.
на левой. А вот двусторонняя асимптота здесь никак не могла бы быть, ведь график симметричен относительно вертикальной оси, т.к. функция чётная.
 =
=  =
= 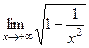 = 1.
= 1.
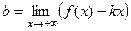 =
=  =
= 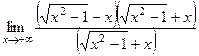
здесь умножили на сопряжённое, как в таких пределах делали раньше.
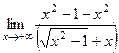 =
= 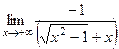 =
= 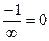 .
.
Итак,  ,
, 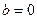 , на правой полуплоскости асимптота
, на правой полуплоскости асимптота 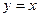 . Тогда из-за симметрии графика чётной функции на левой полуплоскости наклонная асимптота
. Тогда из-за симметрии графика чётной функции на левой полуплоскости наклонная асимптота  .
.
Ответ. Две односторонние асимптоты  и
и  .
.
График (асимптоты показаны зелёным цветом).
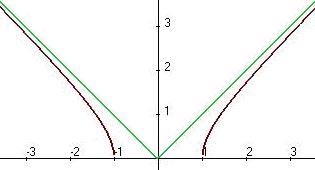
Задача 224. Найти асимптоты графика функции  .
.
Решение. Функция не является чётной, поэтому здесь придётся при  и
и 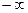 искать пределы каждый отдельно.
искать пределы каждый отдельно.
 =
= 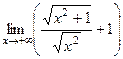 =
=  =
=  .
.
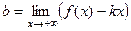 =
=  =
= 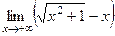 =
=
 =
=  =
=  = 0.
= 0.
Итак, 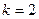 ,
,  , на правой полуплоскости асимптота
, на правой полуплоскости асимптота  .
.
На левой полуплоскости:
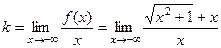 =
=  =
=
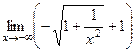 =
= 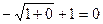 .
.
 =
= 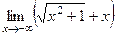 =
= 
=  =
= 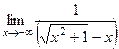 но так как
но так как 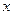 отрицательно то
отрицательно то
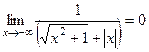 . Итак, на левой полуплоскости
. Итак, на левой полуплоскости 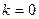 ,
,  . Здесь не наклонная, а горизонтальная асимптота,
. Здесь не наклонная, а горизонтальная асимптота,  .
.
Ответ. На правой полуплоскости наклонная асимптота  ,
,
на левой горизонтальная асимптота  .
.

Задача дом-1. Найти асимптоты графика функции 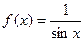 .
.
Ответ. Вертикальные асимптоты 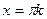 .
.
Задача дом-2. Найти асимптоты графика функции  .
.
Ответ. Вертикальная:  . Наклонная:
. Наклонная:  .
.
Практика 22.
Дифференциальное исчисление функции одной переменной.
Дифференциал, уравнение касательной. Метод Лопиталя.
 =
= 

Законы дифф. суммы и разности, произведения, частного.
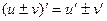 .
. 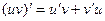 .
.  .
.
Закон дифференцирования композиции, обратной функции.
 .
. 
Задача 225. Вывести формулу  .
.
Решение. По определению, 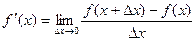 для этой функции надо записать так:
для этой функции надо записать так: 
преобразуем:  =
= 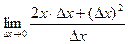 =
= 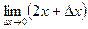 =
= 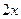 . Итак,
. Итак,  .
.
Задача 226. Доказать, что  . Решение.
. Решение. 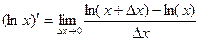 =
= 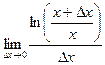 =
= 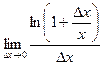 Так как следующие бесконечно малые эквивалентны:
Так как следующие бесконечно малые эквивалентны: 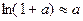 то получим, заменяя на эквивалентную:
то получим, заменяя на эквивалентную: 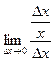 =
= 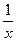 .
.
Задача 227. Доказать, что  .
.
Запишем производную по определению.
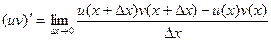
Но тут есть сдвиг на 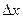 и по u, и по v. Добавим и вычтем такое слагаемое, в котором сдвиг по одной функции есть, а по второй нет:
и по u, и по v. Добавим и вычтем такое слагаемое, в котором сдвиг по одной функции есть, а по второй нет:
 теперь слагаемых стало 4, но зато их можно сгруппировать по два, и даже разбить на две дроби, так, что дельта прибавляется только на одном из мест.
теперь слагаемых стало 4, но зато их можно сгруппировать по два, и даже разбить на две дроби, так, что дельта прибавляется только на одном из мест.
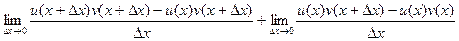
Теперь можно вынести тот множитель, который одинаков в каждой разности:

Видно, то, что осталось в дробях, это и есть производные для u или v соответственно, т.е. в итоге:
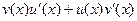 . Итак,
. Итак, 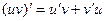 .
.
Задача 227-Б. Вывести формулу 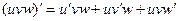 .
.
Решение. Объединим первые 2 слагаемых в один условный множитель, а третье пусть будет вторым множителем. После этого применим известную формулу, доказанную для 2 множителей.
 =
= 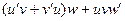 , что и приводит к
, что и приводит к
выражению  .
.
Задача 228. С помощью определения доказать, что  .
.
Решение. 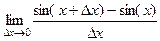 =
=  =
=
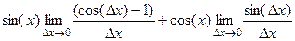 =
=
воспользуемся тригонометрической формулой понижения степени  :
:
 =
=
=  =
=
=  =
=  .
.
Ответ. 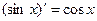 .
.
Задача 229. Вычислить производную от композиций:
А) 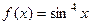 . Б)
. Б) 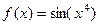
Решение. А)  =
=  =
=  .
.
Б) 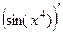 =
=  =
= 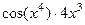 .
.
Ответы.  ;
; 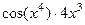 .
.
Задача 230. Найти производную от  .
.
Решение. Здесь композиция трёх функций. Сначала действует степенная и переводит 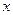 в
в  , затем вычисляется косинус, а от этого выражения зависит логарифм.
, затем вычисляется косинус, а от этого выражения зависит логарифм.
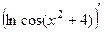 =
= 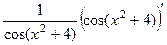 =
=  =
= 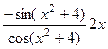 , что можно записать в виде
, что можно записать в виде 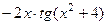 .
.
Ответ.  .
.
Задача 231. Найти производную функции  .
.
Решение. Способ 1. Можно рассматривать как композицию, тогда:
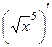 =
=  =
= 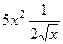 =
=  =
= 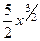 .
.
Способ 2. Можно рассматривать сразу как степенную функцию с дробной степенью, тогда решение такое: 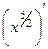 =
= 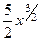 .
.
Как мы видим, двумя способами получаем одно и то же.
Ответ. 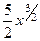 .
.
Задача 232. Найти 1 и 2 производную от 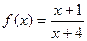 .
.
Решение. 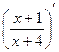 =
=  =
=
 =
=  , что можно записать в виде
, что можно записать в виде 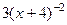 .
.
Вторая производная:  =
=  =
=  .
.
Ответ. 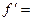

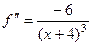 .
.
Задача 233. Найти производную от 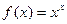 .
.
Решение. Здесь нельзя применять формулу степенной функции, ведь в показателе тоже есть переменная. Но нельзя и формулу показательной функции, т.к. в основании тоже есть переменная. Единственным выходом здесь является логарифмирование, чтобы  осталось только в степени. Основание может быть представлено в виде
осталось только в степени. Основание может быть представлено в виде  . Тогда
. Тогда 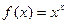 =
= 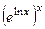 =
=  .
.
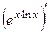 =
= 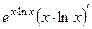 =
= 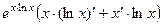 =
=
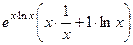 а теперь можем заменить обратно
а теперь можем заменить обратно 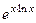 на
на 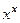 .
.
После приведения подобных, получим  .
.
Ответ.  .
.
Задача 234. Найти 1-ю и 2-ю производную для 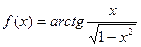 . Найти
. Найти  .
.
Решение.  =
=  =
=
=  =
=
= 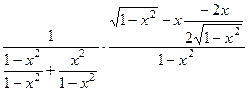 =
=
= 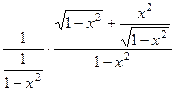 =
= 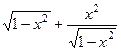 =
=  =
=
 . Итак,
. Итак, 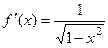 .
.
Следующая, 2-я производная:
 =
=  =
= 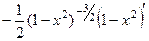 =
=
 =
= 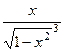 .
.
Вычислим «тестовое» значение при конкретном 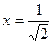 .
.
 =
= 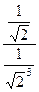 =
= 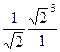 =
= 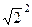 = 2.
= 2.
Ответ. 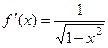 ,
,  ,
,  =2.
=2.
Задача домашняя. Найти 1-ю и 2-ю производную для 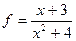 .
.
Ответ. 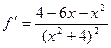
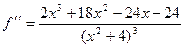
- - - Перерыв - - -
Задача 235. Найти 1-ю и 2-ю производную 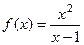 и
и 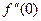 .
.
Решение. 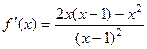 =
=  .
.
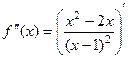 =
= 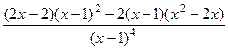 =
=
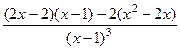 =
=  =
=
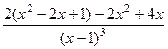 =
= 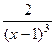 .
.  .
.
Ответ.  ,
,  ,
, 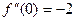 .
.
Задача 236. Дана функция  .
.
Найти 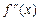 ,
,  .
.
Решение. 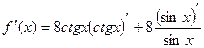 =
= 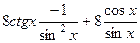 =
=
 =
= 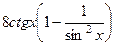 =
= 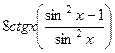 =
=
=  =
=  .
.
Максимально возможно привели подобные, чтобы затем было легче считать 2-ю производную.
 =
= 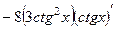 =
=  =
=
=  =
=  .
.
Вычислим 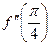 .
.  =
= 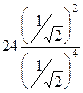 =
=  = 48.
= 48.
Ответ. 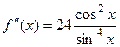 .
. 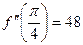 .
.
Задача 237. Нарисовать график  , если функция
, если функция 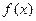 задана графически:
задана графически:
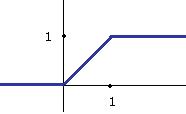
Решение. Здесь мы можем рассуждать следующим образом. Запишем функцию на каждом из участков:

Тогда можно найти производную на каждом участке отдельно:

Тогда график производной выглядит так:

Функция называется дифференцируемой в точке 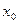 , если приращение можно представить в виде:
, если приращение можно представить в виде:
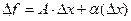
где 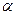 - бесконечно малая более высокого порядка, чем 1-й.
- бесконечно малая более высокого порядка, чем 1-й.
Главная линейная часть приращения функции, а именно  , называется дифференциалом функции
, называется дифференциалом функции 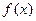 в точке
в точке 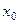 .
.
Обозначается также через  .
.
(Вспомнить: главная часть бесконечно-малой).
Примечание. Бывают не дифференцируемые функции, например 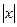 не дифф. в нуле. Нет общей касательной для двух частей графика, правой и левой. Какую бы прямую мы ни провели через (0,0), она не будет касательной к графику функции. Если наклон +450 то есть
не дифф. в нуле. Нет общей касательной для двух частей графика, правой и левой. Какую бы прямую мы ни провели через (0,0), она не будет касательной к графику функции. Если наклон +450 то есть 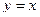 то разность между ней и левой половиной графика не будет бесконечно-малой: эта прямая является касательной к одной части графика, то она перпендикулярна другой ветви этого же графика.
то разность между ней и левой половиной графика не будет бесконечно-малой: эта прямая является касательной к одной части графика, то она перпендикулярна другой ветви этого же графика.
Уравнение касательной. 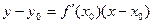 .
.
В этом уравнении, 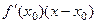 =
=  это фактически и есть дифференциал.
это фактически и есть дифференциал.
Дата добавления: 2020-12-22; просмотров: 542; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
