Выпуклость, вогнутость графика функции, точки перегиба
Пусть f(x) – функция, дифференцируемая на интервале (a, b). Рассмотрим кривую, являющуюся графиком функции y = f(x).
Кривая, заданная функцией y = f(x), называется выпуклой на интервале (a, b), если все точки кривой лежат ниже любой ее касательной на этом интервале.
Кривая называется вогнутой на интервале (a, b), если все точки кривой лежат выше любой ее касательной на этом интервале.
Точка кривой M0(x0, f(x0)), отделяющая выпуклую ее часть от вогнутой, называется точкой перегиба.
Теорема 1. (Достаточные условия выпуклости и вогнутости графика функции).
Если во всех точках интервала (a, b) вторая производная функции f(x) отрицательна, т.е. f''(x) < 0, то кривая y = f(x) на этом интервале выпукла.
Если во всех точках интервала (a, b): 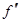 (x) > 0, то кривая y = f(x) на этом интервале вогнута.
(x) > 0, то кривая y = f(x) на этом интервале вогнута.
Теорема 2 (достаточное условие точки перегиба)
Пусть кривая является графиком функции y = f(x). Если 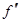 (x0) = 0 или
(x0) = 0 или 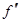 (x0) не существует и при переходе через x0 вторая производная
(x0) не существует и при переходе через x0 вторая производная 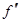 (x) меняет свой знак, то точка M0(x0, f(x0)) этой кривой является точкой перегиба.
(x) меняет свой знак, то точка M0(x0, f(x0)) этой кривой является точкой перегиба.
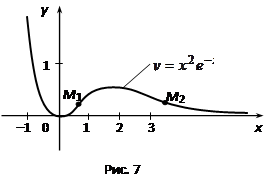
Пример. Исследовать на выпуклость, вогнутость и точки перегиба график функции y = x2e –x.
Решение f(x) = x2e –x,
f'(x) = 2xe –x – x2e –x, f''(x) = = 2e –x – 2xe –x – 2xe –x + x2e –x = e –x(2 – 4x + x2).
Найдем значения x, при которых 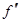 (x) = 0 и интервалы знакопостоянства второй производной
(x) = 0 и интервалы знакопостоянства второй производной 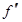 (x):
(x): 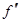 (x) = 0,
(x) = 0,  e - x(2 - 4x + x2) = 0,
e - x(2 - 4x + x2) = 0,
Корни этого уравнения: x1= 2 – 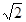 » 0,58 и x2 = 2 +
» 0,58 и x2 = 2 + 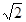 » 3,41.
» 3,41.
Значения функции f (x) в точках x1, x2: y1 = f(x1) » 0,34 и y2 = f(x2) » 0,38.
|
|
|
Результаты исследования занесем в таблицу:
| x | 
| 
| 
| 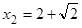
| 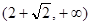
|
| f»(x) | f»(x) > 0 | f»(x1) = 0 | f»(x) < 0 | f»(x2) = 0 | f»(x) > 0 |
| f(x) | Кривая вогнутая | M1(x1, y1) – точка перегиба | Кривая выпуклая | M2(x2, y2) – точка перегиба | Кривая вогнутая |
Построим график функции y = x2e –x рис. (7) с учетом исследования примера
Дата добавления: 2020-12-22; просмотров: 55; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
