Возрастание и убывание функций
Основные теоремы о дифференцируемых функциях
Теорема Ферма. Пусть функция f(x) определена, непрерывна на интервале (a, b) и в некоторой точке x0 этого интервала принимает свое наибольшее или наименьшее значение. Если в точке x0 существует производная этой функции, то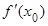 
= 0.
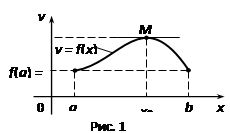Геометрически теорему Ферма поясняет рис. 1. В точке x1 функция принимает наибольшее значение M, а в точке x2 – наименьшее значение m, касательные к графику y = f (x) в точках A и B параллельны оси Ox, так как f'(x1) = 0 и f'(x2) = 0.
Теорема Ролля. Если функция f(x) непрерывна на отрезке [a, b], дифференцируема в каждой внутренней точке и f(a) = f(b), то существует, по крайней мере, одна внутренняя точка x0 отрезка [a, b], что f'(x0) = 0
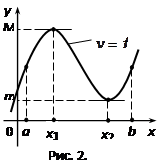
Геометрически теорема Ролля утверждает (рис. 2), что если функция непрерывная на [a, b] и дифференцируемая на (a, b), имеет на концах отрезка [a, b] одинаковые значения, то найдется точка x0 Î (a, b), для которой касательная к графику параллельна оси абсцисс.
Теорема Лагранжа. Если функция f(x) непрерывна на отрезке [a, b], дифференцируема на интервале (a, b), то найдется хотя бы одна внутренняя точка x0 отрезка
[a, b], такая, что =.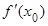 
. (1)
Поясним теорему Лагранжа геометрически (рис. 3). 
Отношение есть угловой коэффициент tga хорды AB, соединяющей точки A(a, f(a)), B(b, f(b)), f'(x0) – угловой коэффициент касательной к графику y = f(x), проведенной в точке M0(x0, f(x0)), и 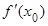= tga. Теорема Лагранжа утверждает, что на графике функции y = f(x) найдется хотя бы одна точка M0, в которой касательная к графику параллельна хорде AB.
|
|
|
Заметим, что формулу (1) можно записать в виде:
f(b) – f(a) = 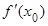(b – a). (2)
Обозначив x0 = c, a = x0, b – a = Dx, b = x0 + Dx, из формулы (2) получаем формулу: f(x0 + D x) – f(x0) = 
(c)D x. (3)
Формулы (2), (3) называют формулами конечных приращений, а теорему Лагранжа – теоремой о конечных приращениях. При этом теорема Лагранжа можно сформулировать следующим образом: приращение дифференцируемой функции на отрезке равно произведению длины отрезка на значение производной этой функции в некоторой внутренней точке отрезка.
Следствие. Если функция f(x) непрерывна на отрезке [a, b] и во всех внутренних точках этого отрезка (x) = 0, то функция f(x) постоянна на отрезке [a, b].
Теорема Коши. Пусть функции f(x), g(x) непрерывны на отрезке [a, b], дифференцируемы на (a, b), причем g'(x) ¹ 0 для любой точки x из интервала (a, b). Тогда существует внутренняя точка x0 отрезка [a, b], такая, что
= 
.
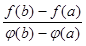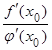Ранее познакомились с приемами раскрытия неопределенностей типа 
и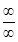 
. Рассмотрим новый способ вычисления таких пределов, так называемое правило Лопиталя.
Теорема Лопиталя. (Раскрытие неопределенностей типа )
Пусть функции f(x), g(x) определены, непрерывны и дифференцируемы в точке x0 и некоторой ее окрестности, причем g'(x) ¹ 0 для любого x из этой окрестности, и пусть f(x0) = 0, g(x0) = 0 (следовательно, f(x), g(x) – бесконечно малые при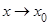 
). Если 
существует, то существует 
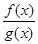и = .
|
|
|
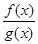Пример 1. Найти 
.
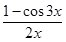Решение. Поскольку функции f(x) =1 – cos3x, g(x) = 2x удовлетворяют условию теоремы Лопиталя, то = 
= 
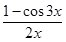= 0.
Замечание 1. Теорема Лопиталя справедлива и в том случае, когда функции f(x), g(x) не определены в точке x0, но f(x) = 0 и g(x) = 0.
Теорема Лопиталя. (Раскрытие неопределенностей типа )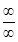
Пусть функции f(x), g(x) дифференцируемы в окрестности точке x0, за исключением самой точки x0, причем g'(x) ¹ 0, и пусть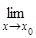 
f(x) = ¥, g(x) = ¥. Если существует 
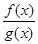, то существует и = .
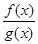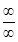Замечание 2. Если при x ® x0 (x ® ¥) является неопределенностью типа или , и (x), g'(x) удовлетворяют условиям теоремы Лопиталя, то = = 
.
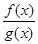То есть раскрытия неопределенностей типа или 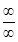иногда приходится применять правило Лопиталя несколько раз.
Пример 2. Найти 
.
Решение. При x ® 0 и x > 0 lnx = ¥, ctgx = ¥, следовательно, имеем отношение двух бесконечно больших при x ® 0 и неопределенность типа 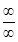. Вычислим:
= 
= – 
= – 
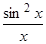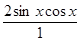= 0.
Пример 3. Найти 
.
Решение. Имеем неопределенность типа 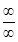. Применяя теорему Лопиталя два раза, получим: 
= 
= 
= ¥.
|
|
|
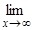
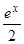. Согласно следствию из теоремы Лагранжа, если производная (x) = 0 на некотором интервале, то функция f(x) постоянна на этом интервале.
Возрастание и убывание функций
Теорема 1. (Достаточное условие возрастания функции)
Если функция f(x) непрерывна на отрезке [a, b] и дифференцируема на интервале (a, b), причем (x) > 0 для любого xÎ(a, b), то эта функция возрастает на отрезке [a, b].
Дата добавления: 2020-12-22; просмотров: 71; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!