Теорема 2. (Необходимое условие возрастания функции)
 Если функция f(x) непрерывна и возрастает на отрезке [a, b], дифференцируема на интервале (a, b), то
Если функция f(x) непрерывна и возрастает на отрезке [a, b], дифференцируема на интервале (a, b), то  (x) ³ 0 для любого x из интервала (a, b).
(x) ³ 0 для любого x из интервала (a, b).
Пример . Исследовать на монотонность (т.е. возрастание и убывание) функцию:
f (x) = x3 – 3x.
Решение.  (x) = 3x2 – 3 = 3(x2 – 1).
(x) = 3x2 – 3 = 3(x2 – 1).
Неравенство  (x) > 0, т.е. 3(x2 – 1) > 0, справедливо для x < –1 и для x >1. Следовательно, функция f(x) возрастает на интервалах (–¥, –1) и (1, +¥). Поскольку неравенство
(x) > 0, т.е. 3(x2 – 1) > 0, справедливо для x < –1 и для x >1. Следовательно, функция f(x) возрастает на интервалах (–¥, –1) и (1, +¥). Поскольку неравенство  (x) < 0, т.е. 3(x2 – 1) < 0 справедливо для xÎ(–1, 1), то на интервале (–1, 1) функция f(x) убывает.
(x) < 0, т.е. 3(x2 – 1) < 0 справедливо для xÎ(–1, 1), то на интервале (–1, 1) функция f(x) убывает.
Построим график функции y = x3 – 3x (рис. 4), используя ее значения в точках:
x1 = –1, x2 = 1, x3 = 0, x4 = – 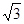 , x5 =
, x5 = 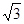 : f(–1) = 2, f(1) = –2, f(0) = 0, f(–
: f(–1) = 2, f(1) = –2, f(0) = 0, f(– 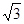 ) = 0, f(
) = 0, f( 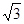 ) = 0.
) = 0.
Заметим, что в точке x1 = –1 значение f (–1) больше, чем значение f(x) в соседних с x1 точках. Говорят, что в точке x1 функция имеет максимум (локальный максимум). Аналогично, f(x2) < f(x) для x, близких к x2. В этом случае говорят, что в точках x2 функция имеет минимум (локальный минимум).
Экстремумы функции
Пусть функция f(x) определена на промежутке X и x0 Î X.
Говорят, что в точке x0 функция f(x) имеет максимум, если существует такая окрестность точки x0, что для любого x из этой окрестности f(x) < f(x0).
Точка x0 называется точкой минимума, если существует такая окрестность точки x0, что для любого x из этой окрестности f(x) > f(x0).
Точки максимума и минимума называются точками экстремума.
Замечание. Точки экстремума всегда являются внутренними точками промежутка, т.е. не могут быть его концом.
|
|
|
Теорема 1. (Необходимое условие экстремума)
Если функция f(x) дифференцируема в точке x0 и некоторой ее окрестности и
x0 – точка экстремума, то  (x0) = 0.
(x0) = 0.
 Следствие. Если x0 – точка экстремума, то
Следствие. Если x0 – точка экстремума, то  (x0) = 0 или
(x0) = 0 или  (x0) не существует.
(x0) не существует.
В качестве примера приведем функцию f(x) = |x| (рис. 5).
Очевидно, что x0 = 0 является точкой минимума, так как |0| < |x| для любого x ¹ 0. А в точке x0 = 0 производной f'(0) не существует.
Если f'(x0) = 0 или f'(x0) не существует, то точку x0 будем называть критической (или подозрительной на экстремум). Критическая точка может и не быть точкой экстремума.
Теорема 2. (Первое достаточное условие экстремума)
Пусть функция f (x) определена и непрерывна в точке x0 и некоторой ее окрестности, дифференцируема в этой окрестности, за исключением, может быть, точки x0, и x0 – критическая точка для функции f (x) (т.е.  (x0) = 0 или
(x0) = 0 или  (x0) не существует). Тогда: 1) если при x < x0 производная
(x0) не существует). Тогда: 1) если при x < x0 производная  (x) > 0, а для x > x0:
(x) > 0, а для x > x0:  (x) < 0, то x0 – точка максимума; 2) если при x < x0:
(x) < 0, то x0 – точка максимума; 2) если при x < x0:  (x) < 0, а при x > x0:
(x) < 0, а при x > x0:  (x) > 0, то x0 – точка минимума.
(x) > 0, то x0 – точка минимума.
Теорема 3. (Второе достаточное условие экстремума).
Пусть функция f (x) дважды дифференцируема в точке x0 и некоторой ее окрестности и пусть  (x0) = 0. Если
(x0) = 0. Если  (x0) > 0, то x0 – точка минимума. Если
(x0) > 0, то x0 – точка минимума. Если  (x0) < 0, то x0 – точка максимума.
(x0) < 0, то x0 – точка максимума.
|
|
|
При исследовании функции на монотонность и экстремумы бывает удобно результаты заносить в таблицу. Как это делается, покажем в следующем примере.
Пример 1. Исследовать на монотонность и экстремумы функцию f(x) = x2e–x. Построить ее график.
Решение. Эта функция определена и непрерывна на всей числовой оси (–¥, ¥). Найдем производную:  (x) = 2xe –x – x2e –x = xe –x(2 – x). Тогда
(x) = 2xe –x – x2e –x = xe –x(2 – x). Тогда  (x) = 0 при x1 = 0 и
(x) = 0 при x1 = 0 и
x2 = 2, где x1, x2 – критические точки. Эти точки разбивают всю числовую ось на три интервала: (–¥; 0), (0; 2), (2; +¥). Составим таблицу, в первой строке которой поместим указанные точки и интервалы, во второй строчке – сведения о производной  (x) в точках и на интервалах, а в третьей – поведение данной функции f(x):
(x) в точках и на интервалах, а в третьей – поведение данной функции f(x):
| x | 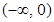
| x1 = 0 | (0, 2) | x2 = 0 | 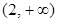
|
 (x) (x)
|  (x) < 0 (x) < 0
| 0 |  (x) > 0 (x) > 0
| 0 |  (x) < 0 (x) < 0
|
| f(x) | убывает | 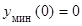
| возрастает | 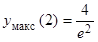
| убывает |
Определим знак  (x) на каждом из интервалов: если xÎ(–¥, 0), то
(x) на каждом из интервалов: если xÎ(–¥, 0), то  (x) < 0; если xÎ(0, 2), то
(x) < 0; если xÎ(0, 2), то  (x)>0; если xÎ(2, +¥), то
(x)>0; если xÎ(2, +¥), то  (x) < 0. Отсюда определяется поведение функции f(x): на первом и последнем интервалах f(x) убывает, а на втором – возрастает. Отсюда следует, что x1 = 0 является точкой минимума, yмин(0) = 0, а x2 = 2 – точка максимума, yмакс(2) =
(x) < 0. Отсюда определяется поведение функции f(x): на первом и последнем интервалах f(x) убывает, а на втором – возрастает. Отсюда следует, что x1 = 0 является точкой минимума, yмин(0) = 0, а x2 = 2 – точка максимума, yмакс(2) = 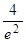 » 0,54. Для построения графика заметим, что f (x) > 0 для всех x, отличных от нуля, и
» 0,54. Для построения графика заметим, что f (x) > 0 для всех x, отличных от нуля, и
|
|
|
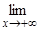 x2e – x = 0,
x2e – x = 0, 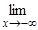 x2e – x = ¥, f(–1) = e » 2,7.
x2e – x = ¥, f(–1) = e » 2,7.
График этой функции изображен на рис. 6.
Отметим, что дальнейшее исследование этой функции (см. следующий раздел) позволит уточнить ее график.
Пример 2. Найти наименьшее и наибольшее значения функции:
f(x) = x4 – 2x2 + 5 на отрезке [–2, 2].
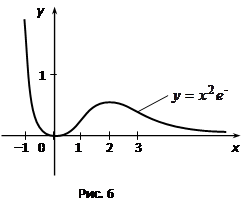 Решение. Найдем критические точки для данной функции:
Решение. Найдем критические точки для данной функции:
 (x) = 4x3 – 4x = 4x(x2 – 1);
(x) = 4x3 – 4x = 4x(x2 – 1);
 (x) = 0 при x1 = 0, x2 = –1, x3 = +1, все три критические точки принадлежат данному отрезку. Вычислим значения функции в точках –2, –1, 0, 1, 2:
(x) = 0 при x1 = 0, x2 = –1, x3 = +1, все три критические точки принадлежат данному отрезку. Вычислим значения функции в точках –2, –1, 0, 1, 2:
f(–2) = (–2)4 – 2×(–2)2 + 5 = 16 – 8 + 5 = 13, f(–1) = 1 – 2 + 5 = 4, f(0) = 5, f(1) = 4, f(2) =13.
Из найденных значений самое малое число 4, а самое большое число 13.
Итак, наименьшее значение функции равно 4, наибольшее значение равно 13.
Пример 3. Найти наибольшее и наименьшее значения функции
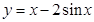 на отрезке
на отрезке  .
.
Решение. 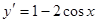 ,
, 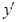 определена во всех точках;
определена во всех точках; 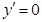 при
при  . На отрезке
. На отрезке 
 при
при 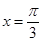 . Имеем три точки:
. Имеем три точки: 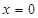 ,
,  ,
,  , в которых могут достигаться наибольшее и наименьшее значения.
, в которых могут достигаться наибольшее и наименьшее значения.
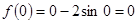 ;
; 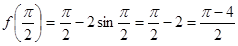 ;
;
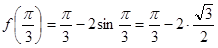 .
.
Итак, 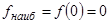 ,
, 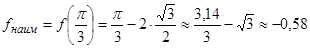 .
.
Дата добавления: 2020-12-22; просмотров: 50; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
