Классификация ошибок измерения
Каждый результат измерения – случайная величина. Отклонение реального результата от истинного называется ошибкой наблюдения. Ошибка наблюдения также является случайной величиной. Она является результатом воздействия неучтенных факторов. Если обозначить истинный результат через a, ошибку – через 
, результат измерения X, то
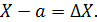
Различают ошибки трех видов:
1) грубые ошибки , которые возникают вследствие нарушения основных условий измерения. Результат, содержащий грубую ошибку, резко отличается от по величине от остальных измерений. На этом основаны некоторые критерии по исключению грубых ошибок.
2) систематические ошибки постоянны во всей серии измерений или изменяются по определенному закону. Выявление их требует специальных исследований, но как только сиситематические систематические ошибки обнаружены, они могут быть устранены путем введения соответствующих поправок в результаты измерения.
3) случайные ошибки – это те ошибки измерения, которые остаются после устранения всех выявленных грубых и систематических ошибок. Они вызываются большим количеством факторов, эффекты воздействия которых столь незначительны, что их нельзя выделить в отдельности ( на данном уровне используемой техники измерения). При этом распределение случайных ошибок симметрично относительно нуля: ошибки, противоположные по знаку, но равные по абсолютной величине, встречаются одинаково часто. Из симметрии распределения ошибок следует, что истинный результат наблюдения есть математическое ожидание соответствующей случайной величины. Так как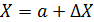 
, и при отсутствии грубых и систематических ошибок 
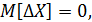то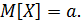 
|
|
|
Случайные ошибки – это те ошибки измерения, которые остаются после устранения всех выявленных грубых и систематических ошибок. Они вызываютсся большим количеством факторов, эффкуты воздействия которых столь незначительны, что их нельзя выделить в отдельности ( на данном уровне используемой техники измерения). При этом распределение случайных ошибок симметрично относительно нуля: ошибки ,противоположные по знаку, но равные по абсолютной величине, встречаются одинаково часто. Из симметрии распределения ошибок следует, что истинный результат наблюдения есть математическое ожидание соответствующей случайной величины. Т.к. 
, и при отсутствии грубых и сиситематических ошибок
то
В дальнейшем будем рассматривать только случайные ошибки измерений.
Закон сложения ошибок
Для независимых случайных величин свойством аддитивности обладают дисперсии, а не среднеквадратичсекие среднеквадратические ошибки. Если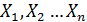 
– независимые случайные величины; 
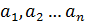– неслучайные величины и
|
|
|
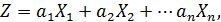
То выборочная дисперсия величины Z определяется следующим образом:
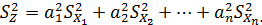
Если положить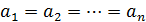 
, то
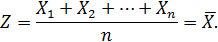
В этом случае
где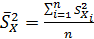 
.
Если 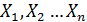интерпретировать как n независимых наблюдений одной и той же случайной величины X, то 
, тогда получим
.
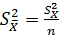Из полученного выражения следует один очень важный практический вывод: при оценке точности двух методов измерений следует учитывать длительность анализа. Применяя менее точные методы можно сделать большее число опытов и получить более точные результаты, чем при использовании трудоемкого точного метода. Можно сделать вывод о возможности уменьшить погрешность окончательного результата при увеличении количества n отдельных измерений. Однако также следует помнить, что повышение точности никогда не дается бесплатно. Так, чтобы узнать дополнительную цифру в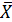 
, т.е. повысить точность в 10 раз, количество измерений необходимо увеличить в 100 раз!
Ошибки косвенных измерений
Измерения делятся на прямые и косвенные. В первом случае непосредственно измеряется определяемая величина, при косвенных измерениях она определяется как функция от непосредственно измеряемых величин. Пусть между случайными величинами z и 
существует известная функциональная зависимость:
|
|
|
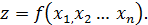
Истинное значение величины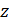 
может не совпадать с математическим ожиданием Mz , а определяется тем же законом:
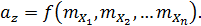
Величина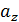 
называется средним косвенного измерения.
Дисперсия косвенного измерения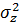 
определяется так же, как обычная дисперсия, только отклонения берутся от среднего косвенного измерения 
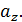Ее можно найти, зная дисперсии отдельных наблюдений и вид функции 
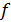. На практике определяют выборочные дисперсии 
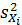и по ним выборочную дисперсию косвенного измерения 
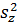, которая служит оценкой генеральной дисперсии 
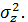Чтобы найти 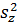, разложим функцию 
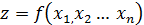в ряд Тейлора в точке ( 
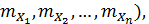ограничившись членами первого порядка:
,
И определим 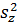по закону сложения дисперсий:
.
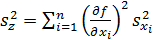Полученное выражение называют законом накопления ошибок.
Дата добавления: 2020-12-22; просмотров: 414; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!