Точечные оценки параметров нормального распределения
Элементы математической статистики
Математическая статистика – раздел математики, изучающий методы сбора, систематизации и обработки результатов наблюдений.
Математическая статистика решает следующие задачи:
1. упорядочение данных , представление их в удобном для обозрения и анализа виде;
2. оценка ,хотя бы приблизительная, интересующих нас характеристик наблюдаемой случайной величины;
3. проверка статистических гипотез, т.е. решение вопроса согласования оценивания с опытными данными (например, проверка гипотезы о том , что наблюдаемая случайная величина подчиняется нормальному закону).
Важнейшей задачей статистики является разработка методов, позволяющих по результатам исследования выборки сделать выводы о параметрах распределения всей совокупности.
Генеральная совокупность и случайная выборка
На практике исследователь обладает лишь ограниченным объемом значений случайной величины, представляющим собой некоторую выборку из генеральной совокупности. Под генеральной совокупностью понимаем все допустимые значения случайной величины. При анализе непрерывной случайной величины (например, температура, давление) под наблюдаемыми значениями случайной величины понимают такие дискретные значения, разделенные определенным интервалом времени, при котором произведенные замеры можно считать независимыми.
Выборка называется репрезентативной, если она дает достаточно полное представление о генеральной совокупности.
|
|
|
В математической статистике доказано (теорема Гливенко), что при достаточно большой выборке функцию распределения вероятностей генеральной совокупности можно заменять функцией распределения выборки.
Числовые характеристики, определенные при ограниченном объеме информации, называются оценками.
Другими словами, на практике мы всегда имеем дело с оценками числовых характеристик случайных величин. Пусть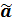 
является оценкой параметра a .
К оценкам числовых характеристик предъявляются следующие требования:
1. Состоятельность – при увеличении числа опытов оценка сходится по вероятности к оцениваемому параметру, т.е. выполняется условие
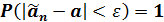при увеличении объема выборки n .
2. Несмещенность – математическое ожидание оценки равно оцениваемому параметру, т.е. при увеличении объема выборки ее математическое ожидание стремится к оцениваемому параметру: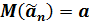 
при увеличении n.
3. Эффективность – несмещенная оценкадолжна обладать минимальной дисперсией по сравнению с другими оценками, т.е.
.
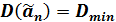Точечные оценки параметров нормального распределения
Как известно, параметрами нормального распределения являются математическое ожидание и дисперсия. В качестве оценки для математического ожидания естественно предположить среднее арифметическое наблюденных значений (выборочное среднее), т.е.
|
|
|
,
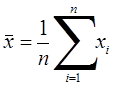которое получается из ранее приведенной зависимости для математического ожидания, если положить
.
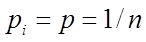В математической статистике доказано, что выборочное среднее является наилучшей (состоятельной, несмещенной и эффективной) оценкой математического ожидания случайной величины, подчиняющейся нормальному закону распределения.
На первый взгляд естественной оценкой для дисперсии D[X]будет
,
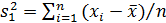Но эта оценка получается несколько смещенной:
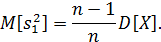
Поэтому для оценки дисперсии используется несмещенная оценка:
.
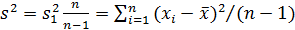Уменьшение знаменателя на единицу непосредственно связано с тем, что величина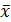 
, относительно которой берутся отклонения, сама зависит от объема выборки. Каждая величина, зависящая от элементов выборки и входящая в формулу, называется связью. В статистике доказывается, что знаменатель выборочной дисперсии всегда равен разности между объемом выборки 
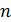и числом связей l , наложенных на эту выборку. Эта разность
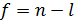
называется числом степеней свободы выборки. В практических вычислениях для оценки дисперсии часто используется более удобная формула:
|
|
|
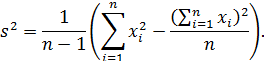
Преимущество этой формулы в том, что в ней нет операций вычитания близких чисел, приводящих к потере точности.
Дата добавления: 2020-12-22; просмотров: 287; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!