Метрики сложности потока управления программ
ЦЕЛЬ РАБОТЫ: оценить сложность программных продуктов с точки зрения оценки сложности потока управления, используя теорию графов, как методическую основу оценки.
ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Вторая, наиболее представленная группа оценок сложности программ – метрики сложности потока управления программ. Как правило, с помощью этих оценок оперируют либо плотностью управляющих переходов, либо взаимосвязями этих переходов.
И в том и в другом случае стало традиционным представление программы в виде управляющего ориентированного графа G = (V, E), где V – вершины, которые соответствуют операторам, а E – дуги, которые соответствуют переходам.
Неупорядоченная пара вершин называется ребром, упорядоченная пара - дугой.
Граф, содержащий только ребра, называется неориентированным; граф, содержащий только дуги - ориентированным (или орграфом).
Пара вершин может быть соединена двумя или более ребрами (или, соответственно, дугами одного направления), такие ребра (или дуги) называются кратными.
Дуга (или ребро) может начинаться и заканчиваться в одной и той же вершине, в этом случае соотв. дуга (или ребро) называется петлей.
Вершины, соединенные ребром или дугой, называются смежными.
Ребра, имеющие общую вершину, тоже называются смежными.
Ребро (или дуга) и любая из его вершин называются инцидентными.
Принято говорить, что ребро (u, v) соединяет вершины u и v, а дуга (u, v) начинается в вершине u и кончается в вершине v.
|
|
|
Цикломатическое число Маккейба
Впервые графическое представление программ было предложено Маккейбом. Основной метрикой сложности он предлагает читать цикломатическую сложность графа программы, или, как ее еще называют цикломатическое число Маккейба, характеризующее трудоемкость тестирования программы.
Для вычисления цикломатического числа Маккейба Z(G) применяется формула
Z ( G ) = e - v +2 p (1)
где e – число дуг ориентированного графа G; v – число вершин; 2 p – число компонентов связности графа.
Число компонентов связности графа можно рассматривать как количество дуг, которые необходимо добавить для преобразования графа в сильносвязнный. Сильносвязным называется граф, любые две вершины которого взаимно достижимы. Для графов корректных программ, т.е. графов, не имеющих недостижимых от точки входа участков и «висячих» точек входа и выхода, сильносвязанный граф получается путём замыкания дугой вершины, обозначающей конец программы на вершину, обозначающую точку входа в эту программу. Как правило, р = 1
По сути Z(G) определяет число линейно независимых контуров в сильносвязном графе. Иначе говоря, цикломатическое число Маккейба показывает требуемое количество проходов для покрытия всех контуров сильносвязного графа или количество тестовых прогонов программы, необходимых для исчерпывающего тестирования по критерию "работает каждая ветвь"
|
|
|
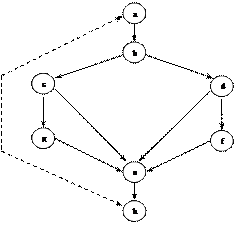Для программы, граф которой
изображен на рисунке 1,
цикломатическое число при e = 10, v = 8, p = 1,
определится как Z(G) = 10-8+2=4. Таким образом, имеется сильносвязный граф с четырьмя линейно независимыми контурами: a - b - c - g - e - h - a ; a - b - c -- e - h - a ; a - b - d - f - e - h - a ; a - b - d - e - h - a .
Цикломатическое число зависит только от количества предикатов, сложность которых при этом не учитывается.
Например, имеется два оператора условия :
IF X>0
THEN X=A;
ELSE;
и
IF (X>0 & FLAG = '1'B) !
(X=0 & FLAG = '0'B)
|
|
|
THEN X=A;
ELSE;
Оба оператора предполагают единственное ветвление и могут быть представлены одним и тем же графом (рис. 2). Очевидно, цикломатическое число будет для обоих операторов одинаковым, не отражающим сложности предикатов, что весьма существенно при оценке программ.
Исходя из этого Г.Майерс предложил расширение этой метрики. Суть подхода Г.Майерса состоит в представлении метрики сложности программ в виде интервала [Z(G), Z(G)+h]. Для простого предиката h ≠ 0, а для n-местных предикатов h=n-1. Таким образом, первому оператору соответствует интервал [2, 2], а второму [2, 6].
Такая метрика позволяет различать программы, представленные одинаковыми графами.
Дата добавления: 2020-04-08; просмотров: 264; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!