Оценка погрешности интерполяционной формулы Лагранжа

Тема 2.3 Интерполирование и экстраполирование функций

Постановка задачи

В вычислительной математике нередки случаи, когда одну функцию приходится заменять другой, более простой и удобной для дальнейшей работы. Такую задачу называют аппроксимацией функций. Поводом для аппроксимации функции может послужить, в частности, табличный способ ее задания.

Пусть на отрезке [a, b] некоторая функция f(x) задана лишь в некоторых точках 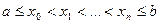, т.е. известны ее значения 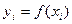, , 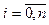которые, как правило, собирают в таблицу:

x	x₀	x₁	...	x_n
f(x)	y₀	y₁	...	y_n

(1)

Кроме того, пусть задана некоторая точка 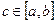, не совпадающая с табличными значениями x_i. Задача аппроксимации функции состоит в том, чтобы по имеющейся таблице найти число с известной степенью точности. Слово «аппроксимация» означает «приближение». Мы будем далее предполагать, что функция обладает всеми производными. Оказывается, что в этом случае по имеющимся n+1 значениям можно найти еще одно и оценить, насколько оно точно.

Если аналитическое выражение функции неизвестно или очень сложное, то прибегают к замене функции f ( x ) на функцию F ( x ), которая в некотором смысле близка к функции f ( x ) и аналитическое выражение которой известно.

Функция F ( x ) называется приближающей функцией.

Классический подход к построению приближающей функции F ( x ) основывается на требовании строгого совпадения значений функций f ( x ) и F ( x ) в точках x_i , i = 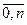, т.е. F ( x ₀ ) = y ₀ , F ( x ₁ ) = y ₁ , … , F ( x_n ) = y_n. Нахождение приближающей функции, удовлетворяющей этому условию, называется интерполированием. Точки x ₀ , x ₁ , …, x_n – узлами интерполирования.

Геометрически интерполирование означает замену графика функции у = f ( x ) графиком y = F ( x ), который должен проходить через все точки A_i ( x_i ; y_i ), i = 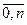. При этом для значений х, не являющихся узловыми, значения функций f ( x ) и F ( x ) могут значительно отличаться.

В такой постановке задача решается неоднозначно. Наиболее простой и изученный класс функций – это класс многочленов. Будем искать интерполирующую функцию в виде многочлена

P_n ( x ) = a ₀ xⁿ + a ₁ xⁿ ^-1 + … + a_n _-1 x + a_n, (2)

который в заданных точках принимает те же значения, что и функция f ( x ), т.е.

P_n ( x_i ) = f ( x_i ), i = 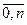. (3)

Интерполяционный многочлен Лагранжа

Пусть функция f ( x ) задана таблицей (1). Построим интерполяционный многочлен L_n ( x ), степень которого не выше п, и для которого выполнены условия интерполяции:

L_n(x₀) = y₀,, L_n(x₁) = y₁, … , L_n(x_n) = y_n. (4)

Будем искать многочлен L_n ( x ) в виде:

L_n(x) = l₀(x) + l₁(x) +…+ l_k(x) + …+ l_n(x), (5)

где вспомогательный многочлен l_k ( x ) – многочлен степени п, причем

l_k ( x_i ) = 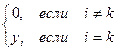(6)

Из этого условия следует, что все узлы интерполирования, кроме x_k, являются нулями многочлена l_k ( x ), поэтому

l_k ( x ) = с_к(х – х₀)(х – х₁)…(х – х_к-1)(х – х_к+1)…(х – х_п) (7)

Из условия (6) найдем C_k:

C_k =

(заметим, что ни один множитель в знаменателе не равен нулю).

Подставим C_k в равенство (7) и далее с учетом (5) окончательно получим:

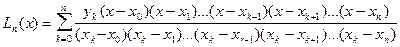(8)

Это и есть интерполяционный многочлен Лагранжа. Равенство f ( x ) ≈ L_n ( x ) – интерполяционная формула Лагранжа.

Оценка погрешности интерполяционной формулы Лагранжа

Заменяя значение функции f ( x ) интерполяционным многочленом Лагранжа, мы допускаем погрешность.

f ( x ) - L_n ( x ) = R_n ( x ). Разность R_n ( x ) называется остаточными членом формулы Лагранжа, который и дает погрешность метода.

Если будет известно, что 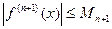, где , то погрешность можно оценить по формуле

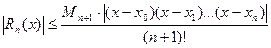(9)

Дата добавления: 2020-11-27; просмотров: 66; Мы поможем в написании вашей работы!

Поделиться с друзьями:

12 3 Следующая ⇒

Мы поможем в написании ваших работ!