Вероятностный характер строительства. Влияние случайных факторов
Вероятностный характер строительства заключается в том, что на ход работ все время воздействуют различные случайные факторы. Эти воздействия трудно предвидеть и оценить. Случайные факторы имеют весьма многообразную природу, и последствия их воздействия весьма многообразны.
Случайные факторы можно классифицировать по следующим категориям:
1. Случайные факторы технического порядка: всевозможные поломки машин, механизмов, деталей, транспортных средств, низкое качество материалов, конструкций, не позволяющее применить их по назначению; изменение проектных решений в процессе строительства.
2. Случайные факторы технологического порядка: устранение брака, переделка недоброкачественно выполненных работ; появление непредвиденных работ.
3. Случайные факторы организационного порядка: нарушение по поставкам материалов, конструкций, срыв согласованных сроков работ, отсутствие рабочих требуемой специальности или квалификации.
4. Случайные факторы климатического порядка.
5. Случайные факторы социального порядка: невыход работника на производство, невыполнение производственного задания при полном обеспечении работ, умышленная порча или хищение материалов, оборудования.
Очень важно оценить воздействие случайных факторов, предвидеть их наступление.
Влияние случайных факторов конкретно выражается в том, что при самом разнообразном сочетании случайных величин и при различной их природе совокупное воздействие, в конечном счете, выражается, в основном, следующим образом: фактическая продолжительность работ и фактические затраты ресурсов на выполнение этих работ отклоняются от значений, принятых в исходных планах и графиках.
|
|
|
Использование метода резервирования для повышения
Надежности
Рассмотрим использование метода резервирования при восстановлении. Чрезвычайные ситуации (ЧС) на железных дорогах приводят к сложным процессам при восстановительных строительных работах. Если имеет место резервный фонд машин, конструкций, бригад и т.д., то при ЧС восстановительный процесс облегчается.
Надежность строительного объекта увеличивается в случае, когда некоторые части объекта можно восстанавливать в процессе работы объекта. Восстановление есть мощное средство повышения надежности при наличии резервного фонда. Уменьшая время восстановления отказавших объектов, имеющих резервный фонд, можно существенно повысить как готовность, так и безотказность объекта.
Особенности восстановления объектов, имеющих резервный фонд, рассмотрим на примере дублированной системы, в которой имеются две одинаковые строительные единицы (бригада, машина, конструкция и т.д.) — основная и резервная.
|
|
|
Предположим, что во время восстановления в строительный единицах (СЕ) не могут возникнуть вторичные отказы. Тогда дублированная система может находиться в одном из трех состояний, которые обозначим цифрами:
О — строительная система работоспособна (СЕ работоспособны);
1 — строительная система работоспособна, но одна СЕ отказала (система стала нерезервированной);
2 — строительная система неработоспособна (отказала).
Обозначим вероятности перечисленных выше состояний через P0(t), P1(t), P2(t). Отметим, что эти вероятности зависят от начального состояния системы, в котором она находилась при t = 0.
В зависимости от назначения резервного фонда к нему могут предъявляться различные требования:
1. С начала производства строительных работ (строительства или реконструкции железной дороги) строительная система должна безотказно функционировать заданное время; перерывы в работе недопустимы. При этом необходимо знать вероятность непрерывной безотказной работы системы (вероятность первый раз не оказаться в состоянии 2). Вычисляем условные вероятности безотказной работы на интервале (0, t) при условии, что при t = 0 основная и резервная СЕ работоспособны.
|
|
|
2. Необходимо, чтобы вероятность застать строительную систему работоспособной в любой заданный момент времени t была достаточно высока (перерывы в работе всей строительной системы не играют существенной роли). При этом рассматриваем готовность строительной системы и ее характеристики: функцию готовности Г(t) или коэффициент готовности k2. Иначе говоря, находиться вероятность не оказаться в состоянии 2. Этот случай отличается от предыдущего тем, что имеется возможность перехода из состояния 2 в состояние 1.
Найдем формулы для функции готовности и вероятности безотказной работы с восстановлением. Предположим, что основная и резервная СЕ равнонадежны, имеют показательные распределения времени безотказной работы и времени восстановления, λ1 = λ2 = λ, μ1 = μ2 = μ, неработающих СЕ невозможны, отказы обнаруживаются мгновенно.
Вначале рассмотрим случаи, где отказы допустимы.
На рис.1.3. приведены графы состояний четырёх возможных вариантов восстанавливаемой строительной системы, имеющей резервный фонд:
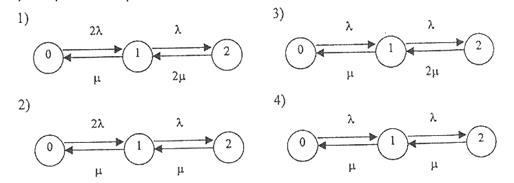
Рис.1.3. Графы состояния различных вариантов восстанавливаемого строительного
|
|
|
объекта, имеющего резервный фонд
1. Нагруженный резервный фонд - при отказах СЕ они могут приводиться в готовность как отдельно, по одному, так и одновременно (восстановление без ограничений);
2. Нагруженный резервный фонд - отказавшие СЕ могут восстанавливаться лишь по одному (ограниченное восстановление);
3. Ненагруженный резервный фонд - восстановление производиться без ограничений;
4. Ненагруженный резервный фонд - восстановление производиться по одной СЕ.
Дифференциальное уравнение для вероятности состояний в соответствии с графами состояний (см. рис.1.5.) имеют вид:
для первого варианта
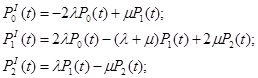 (1)
(1)
для второго варианта
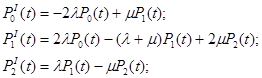 (2)
(2)
для третьего варианта
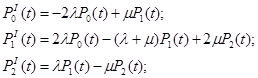 (3)
(3)
для четвертого варианта
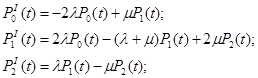 (4)
(4)
Для всех четыре вариантов эти уравнения должны быть дополнены нормирующим условием:
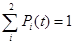 (5)
(5)
Решив уравнения (1)-(5) при начальных условиях Р0(0) = 1; P1(0) = Р2(0) = 0, найдем зависимости Рi(t) для i = 0,1,2.
Для рассматриваемых систем функция готовности
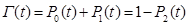 (6)
(6)
Функция готовности рассмотренных выше четырех вариантов резервированных систем с восстановлением имеют вид:
для первого варианта
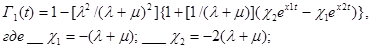 (7)
(7)
для второго варианта
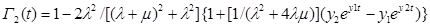 (8)
(8)
для четвертого варианта
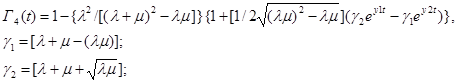 (10)
(10)
На рис.1.4 приведены зависимости Г(t), вычисленные по формулам (7)-(10) для λ=0,01, 1/ч; μ=0,1, 1/ч
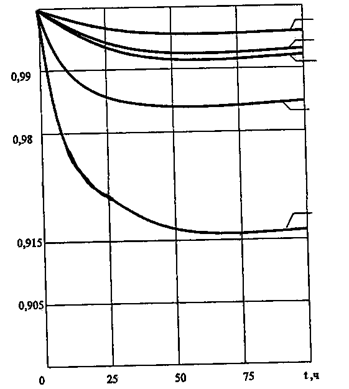
Рис. 1.4. График функции готовности для четырех вариантов восстанавливаемого строительного объекта, имеющего резервный фонд
Для сравнения на графике показана функция готовности Г5(t) строительной системы, не имеющей резервного фонда, с теми же значениями λ и μ.
Обозначив Р = λ / μ из формул (7)-(10) получим:
k21=(1 + 2ρ)/(1 + ρ)2; (11)
k22=(1 + 2 ρ)/[(1 + ρ)2+ ρ 2]; (12)
k23=2(1 + 2 ρ)/[(1 + ρ)2+1]; (13)
k24=(1 + 2 ρ)/[(1 + ρ)2- ρ]. (14)
При ρ = 0,1 соответствующие значения k2 равны 0,992; 0,984; 0,995; 0,991.
Г5(t) — функция готовности соответствующего строительного объекта, не имеющего резервного фонда.
Таким образом, для повышения готовности восстанавливаемой строительной системы, имеющей резервный фонд, необходимо стремиться к созданию условий, обеспечивающих осуществление ненагруженного резервного фонда и восстановление без ограничений.
Для определения условий вероятности безотказной работы составим дифференциальных уравнений при условии, что состояние 2 является поглощающим, т. е. Отсутствуют переходы из состояния 2 в состояние 1. При этом в соответствии с графами состояний (см. рис.1.6) получим:
для первого и второго вариантов
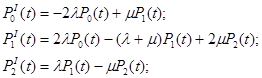 (15)
(15)
для третьего и четвертого вариантов
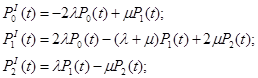 (16)
(16)
При начальных условиях Р0(0) = 1, Р1(0) = Р2(0) = 0 в результате решения систем уравнений (15) и (16) совместно с нормировочным условием (5) получим выражение для условной вероятности безотказной работы:
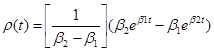 (17)
(17)
где для первого и второго вариантов:
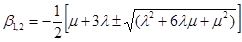 (18)
(18)
для третьего и четвертого вариантов:
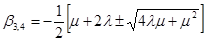 (19)
(19)
Зависимости p(t), вычисленные по формулам (17)-(19) для λ=0,01, 1/ч; μ=0,1, 1/ч приведены на рис.1.5.
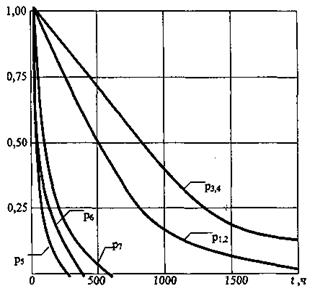
Рис.1.5. График функции надежности различных строительных систем при ненагруженном резервном фонде в зависимости от среднего времени безотказной работы
На рисунке для сравнения приведены графики функций надежности невосстанавливаемых систем: без резервного фонда p5(t), с нагруженным резервным фондом без восстановления p6(t) и ненагруженным резервным фондом без восстановления р7(t).
Если в начальный момент времени (t= 0) все СЕ системы, имеющей резерв, работоспособны, то время безотказной работы есть время перехода из начального состояния в подмножество неработоспособных состояний.
Предположим, что нет ограничений на число ремонтных бригад, отказы обнаруживаются мгновенно, аппаратура контроля безотказна, основная и резервная СЕ равнонадежны и имеют показательные распределения времени безотказной работы и времени восстановления. Применяя известные методы, получаем выражения для среднего времени безотказной работы системы с резервным фондом, состоящей из одной основной и k-1 запасных СЕ: При нагруженном резервном фонде
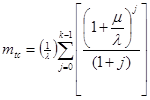 (20)
(20)
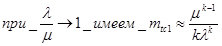 (21)
(21)
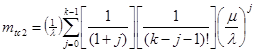 (22)
(22)
 (23)
(23)
В реальных строительных системах могут существовать ограничения по числу ремонтных бригад, общему допустимому числу восстановлений и др. Поэтому значения mtc, вычисленные по формулам (20)-(23), приходится считать верхним пределом среднего времени безотказной работы восстанавливаемой системы, имеющей резервный фонд. Выражения для при г = 1 получены путем составления и решения системы дифференциальных уравнений, соответствующей графу состояний при г = 1.
Сопоставив выражение для среднего времени безотказной работы дублированной восстанавливаемой строительной системы с нагруженным резервным фондом при идеальном контроле согласно (20), со значением среднего времени безотказной работы невосстанавливаемой системы с нагруженным резервом mtc =3/2λ, найдем
mtc / m"tc = 1+μ/3λ = 1+1/3ρ
Таким образом, при ρ = λ/μ = 0,01 - 0,001 применение восстановления повышает среднее время безотказной работы строительной системы, имеющей резервный фонд, в 30-300 раз.
Строительство железных дорог, как и любое другое производство, требует больших объемов поставок различных материалов, конструкций, изделий, топлива и т.п. Для обеспечения ритмичности выполнения работ по сооружению объектов железнодорожного строительства необходимо не только выдерживать определенный темп поставок, но и обеспечивать комплектацию поставляемых конструкций и изделий.
В большинстве случаев трудно обеспечить необходимую ритмичность строительного процесса только за счет регулярности поставок исходных компонентов. Их доставка сопровождается, как правило, сбоями, возникающими по разным причинам: погодные факторы, технические - поломки машин, социальные - невыход на работу и др. Следствием этих сбоев являются срывы плановых или договорных сроков строительства.
Для компенсации возможных отклонений темпа поставки от исходного темпа, определяемого темпом строительства, используют накопление прибывающих материалов, изделий, конструкций и т.п. на складах.
Склады могут быть приобъектными, рассчитанными на хранение относительно небольших объемов материалов в течение срока строительства. Хранение осуществляется, как правило, на открытых площадках, что допустимо для большинства крупногабаритных строительных конструкций. Однако для материалов, требующих особых условий хранения, необходимо предусматривать специальные помещения, что ведет к удорожанию единицы хранения.
Накопление грузов дня группы объектов обычно осуществляется на производственных базах, имеющих капитальные склады, что увеличивает допустимый срок хранения, но и удорожает его, Поэтому решение задачи управления запасами должно обеспечить приемлемую стоимость хранения при обеспечении ритмичного снабжения строительных объектов.
Графическая модель накопления и расходования запасов на складе выглядит следующим образом:
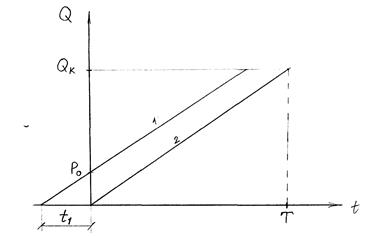
1 - график поставок на склад; 2 - график расходования материалов со склада;
Т - срок строительства; QК - общий объем материалов, израсходованных за время строительства.
Рис.1.6. Графическая модель накопления и расходования запасов на складе
Модель, представленная на рис, описывает функционирование приобъектного склада, который завершает свое существование вместе с окончанием строительства объекта или цикла поставок на склад каких-либо материалов, изделий или конструкций. Началом этого цикла служит момент первой поставки, а завершение происходит вместе с прекращением потребности в данном виде материала.
Исходными параметрами модели являются:
Т – срок строительства;
QК – объем материалов, изделий, конструкций, израсходованных за время
строительства объекта.
Рассчитаем количество рельсов длиной 25 м необходимых для укладки рельсов:
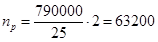 (шт.).
(шт.).
Рассчитаем количество деревянных шпал, исходя из того, что 20% длины строящегося участка приходится на кривые.
На 1 км на прямой укладывается 1840 шпал:
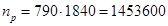 (шп.).
(шп.).
На 1 км на кривой укладывается 2000 шпал:
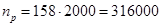 (шп.).
(шп.).
Тогда общий объем необходимых материалов равен
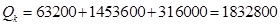 (шт.).
(шт.).
Имея эти исходные данные, можно определить интенсивность расходования материалов со склада.
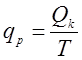
где T = 23,3 сут. – время укладки рельсошпальной решётки краном УК-25.
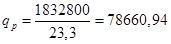
Обычно известна интенсивность потока поставок, либо на нее можно воздействовать в требуемом направлении. Эту интенсивность можно определить следующим образом:
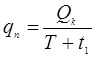 (24)
(24)
Если зафиксировать произвольный момент времени tx, то ему будут соответствовать ординаты Qхр и Qхр, которые, соответственно, покажут, сколько материала (Qхр) к этому моменту было израсходовано и получено (Qхn,) на склад. Разница между ними px = Qxn - Qхп,, покажет, сколько материала на данный момент находится на складе.
Одним из главных назначений склада является выполнение буферной функции, то есть сглаживание неравномерности потока поставок для обеспечения ритмичности снабжения объектов строительства. Понятно, что, чем больше объем склада, тем лучше он будет выполнять буферную функцию.
С другой стороны, увеличение объема склада удорожает хранение. Кроме того, реальная ситуация может накладывать ограничения на максимальный объем склада, Например, на 100 м пути можно разместить три пакета звеньев путевой решетки длиной по 25 м; выделив один станционный путь длиной 850 м под склад, мы тем самым ограничиваем его объем девятью пакетами звеньев, что сопоставимо со сменной выработкой на укладке пути.
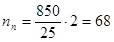 (шт.);
(шт.);
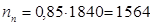 (шп.).
(шп.).
Общий объем необходимых материалов:
Pо = 68 + 1564 = 1632 (шт).
С точки зрения выполнения складом буферной функции, важным является создание до начала строительства первоначального запаса Р0 , который будет находиться на складе в момент времени Т0 начала строительства. Для обеспечения этого запаса поставки на склад необходимо начать за t1 дней до начала строительства.
Определить срок t1 можно, зная режим поставок на склад. В приведенном на рис случае поставки завершаются в момент завершения строительства. Поэтому время t1 можно определить как
 . (25)
. (25)
Однако работа склада в таком режиме, как на рис, снижает надежность бесперебойного снабжения строительства по мере приближения к его завершению за счет постоянного сокращения буферного запаса.
Для повышения надежности снабжения следует ограничить объем склада так, чтобы не допустить его, снижения. Так как объем материалов, прошедший через склад, должен быть равен израсходованному строителями, то поставки на склад должны быть завершены до окончания строительства.
В данном случае удобно считать, что qn = qp , и, зная Р0 как минимально допустимый запас на складе, время начала поставок можно определить как
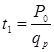 (26)
(26)
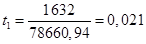 (сут.);
(сут.);
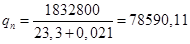
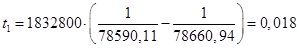 (сут.).
(сут.).
 | |||
 | |||
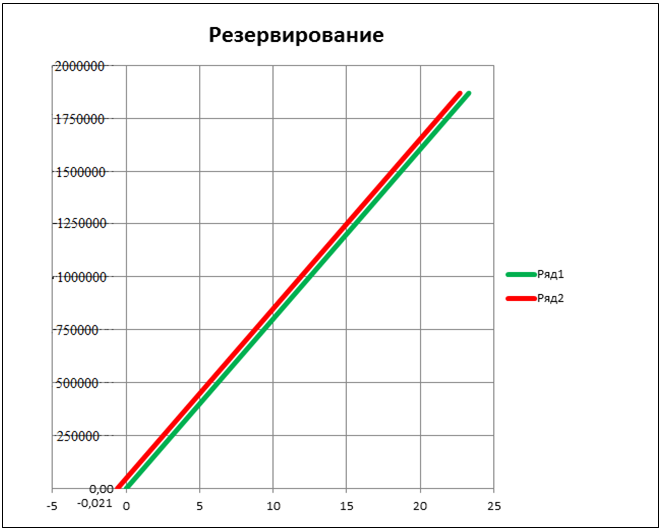
Наиболее сложной модель управления запасами становится тогда, когда необходимо учесть сезонные колебания темпа строительства и связанные с этим колебания расхода материалов со склада.
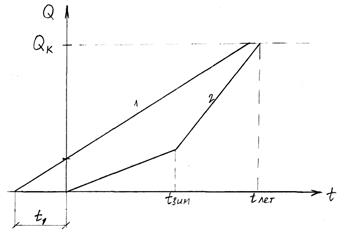
Рис.1.8. Графическая модель накопления и расходования запасов с учетом сезонных колебаний
Будем считать, что зимний расход материала меньше, а летом больше. Тогда модель будет выглядеть следующим образом. Эта модель построена в предположении, что интенсивность потока поставок постоянна, меняется только интенсивность расхода. При этом из чертежа видно, что
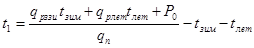 (27)
(27)
Максимальный объем склада при этом составит:
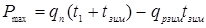 . (28)
. (28)
Дата добавления: 2020-11-23; просмотров: 228; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
