Вопросы и упражнения для самостоятельной работы (самоконтроля)
Определение переходного тока по известному операторному току
В задачах электротехники операторные токи представляются в виде рациональных дробей, числители и знаменатели которых являются полиномами комплексной переменной p:

где M ( p ) - полином степени m , N ( p ) - полином степени n; всегда m < n . Чтобы найти соответствующий переходный ток, дробь нужно разложить на сумму простейших дробей:

Здесь А1,А2,…, An - некоторые постоянные, p 1 , p 2 ,…, pn - корни уравнения N ( p )=0. Полином n-ой степени N ( p ) имеет n корней и может быть представлен в виде N ( p )=( p - p 1 )( p - p 2 )…( p - pn ). Коэффициент при степени pn всегда можно сделать равным единице, разделив числитель и знаменатель дроби на величину возможного неединичного коэффициента при этой степени.
Примечание. При расчете цепей с постоянным ЭДС операторным методом знаменатели операторных токов имеют вид N ( p )= pN 1 ( p ), где N 1 ( p )-полином степени n -1,если степень полинома N ( p ) равна n . В этом случае полином N ( p ) имеет корень p 1 =0, а первому слагаемому в формуле (36) соответствует постоянная составляющая переходного тока.
При расчете цепей с синусоидальными ЭДС знаменатели операторных токов имеют вид N ( p )=( p 2 +ω2) N 2 ( p ), где ω-круговая частота ЭДС, степень полинома N 2 ( p ) равна n -2, если степень полинома N ( p ) равна n . В этом случае уравнение N ( p )=0 имеет корни p 1 = jω и p 2 =- jω , а двум первым слагаемым в формуле (36) соответствует синусоидальная составляющая переходного тока.
Постоянные А1,А2,…,Аn в формуле (36) можно найти методом неопределенных коэффициентов, как было показано в примере 1.5. Если степень полинома N(p) больше двух, то рациональнее воспользоваться другим методом для определения этих постоянных, вычислить их с помощью теоремы разложения рациональных дробей.
| И 1.29 | В разложении рациональной дроби на простейшие дроби  коэффициенты А k при всех k от 1 до n определяются по формуле
коэффициенты А k при всех k от 1 до n определяются по формуле  где
где  и и  . .
|
Доказательство теоремы. Умножим обе части равенства (37) на 

Теперь перейдем к пределу при  . В правой части равенства все дроби обращаются в ноль и остается только коэффициент Ak .Значит,
. В правой части равенства все дроби обращаются в ноль и остается только коэффициент Ak .Значит,

Этот предел приводит к неопределенности вида  , так как N ( pk )=0 ( pk -корень полинома N ( p )). По правилу Лопиталя получаем, что
, так как N ( pk )=0 ( pk -корень полинома N ( p )). По правилу Лопиталя получаем, что

В последнем выражении 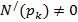 , если полином N ( p ) не имеет кратных корней. Проверим это утверждение на простом примере:
, если полином N ( p ) не имеет кратных корней. Проверим это утверждение на простом примере:

если корни полинома различны, то в пределе при  получаем
получаем

Таким образом, формула (38) доказана, но только при условии, что знаменатель рациональной дроби N ( p ) не имеет кратных корней.
После того как выражение для операторного тока разложено на простейшие дроби, по правилу 6 преобразования Лапласа находятся экспоненциальные составляющие переходного тока:

Среди корней характеристического уравнения pk может оказаться пара комплексных сопряженных чисел. Пусть это будут корни p 1 =-δ+ jω и p 2 =-δ- jω ; в этом случае коэффициенты  и
и  являются комплексными сопряженными числами. Две экспоненты с комплексными сопряженными показателями следует преобразовать в затухающую синусоиду с помощью формулы Эйлера:
являются комплексными сопряженными числами. Две экспоненты с комплексными сопряженными показателями следует преобразовать в затухающую синусоиду с помощью формулы Эйлера:

Частный пример такого преобразования был рассмотрен в п. 1.6.6.
Примечание. При расчете переходных процессов нередко встречаются особенности, которые требуют особого подхода. При первом знакомстве с теорией переходных процессов уделять внимание всем этим особенностям нецелесообразно. Достаточно, например, иметь ввиду, что при наличии у характеристического уравнения кратных корней формула (38) неверна. Не следует однако впадать в крайность и думать, что изложенные выше основы теории переходных процессов из-за множества исключений не имеют существенного практического значения. На практике при расчете переходных процессов пользуются справочниками, электротехническими или математическими. В них имеются обширные таблицы преобразования Лапласа (прямого и обратного) и отмечены многие особенности его применения.
Вопросы и упражнения для самостоятельной работы (самоконтроля)
1. Запишите разложение операторного тока на простейшие дроби (36) в случае, когда переходный процесс происходит в цепи с источником постоянного напряжения и переходный ток имеет постоянную составляющую.
2. Запишите операторный ток, соответствующий синусоидальному току  . Разложите полученное выражение на простейшие дроби. (Указание: см. правила преобразования Лапласа 8 в п. 1.7.2.).
. Разложите полученное выражение на простейшие дроби. (Указание: см. правила преобразования Лапласа 8 в п. 1.7.2.).
3. Запишите разложение операторного тока на простейшие дроби (36) в случае, когда переходный процесс происходит в цепи с источником синусоидального напряжения и переходный ток имеет синусоидальную составляющую.(Указание: используйте выражение для операторного тока, соответствующего синусоидальному току, и его разложение на простейшие дроби).
4. Выпишите выражение для операторных токов из примера 1.5. Разложите их на простейшие дроби с помощью теоремы разложения (по формуле (38)).
5. Запишите в операторной форме уравнение (11) с начальными условиями (12) и (13) (вместе они описывают разряд конденсатора через катушку). Найдите операторный ток, запишите его выражение в случае когда  (точнее, с помощью этой формулы исключите из выражения для операторного тока параметр С). Запишите переходный ток в рассматриваемом случае – формула (24). Сравнивая операторный и переходный токи, убедитесь в соответствии
(точнее, с помощью этой формулы исключите из выражения для операторного тока параметр С). Запишите переходный ток в рассматриваемом случае – формула (24). Сравнивая операторный и переходный токи, убедитесь в соответствии  .
.
Переходная проводимость
Предварительные замечания. В цепях с источниками постоянного или синусоидального напряжения легко разделяются установившиеся и свободные составляющие переходных токов. Обычно установившиеся синусоидальные токи рассчитывают символическим методом, а свободные токи - операторным методом. Расчет переходного процесса усложняется, если в цепи действует переменная несинусоидальная ЭДС. При решении задачи классическим методом возникают затруднения с определением установившихся токов (частного решения дифференциального уравнения). Применение операторного метода наталкивается на расчет изображений сложных функций времени, а затем на трудности обратного перехода от изображений к оригиналам. Дать какие-либо рекомендации общего характера невозможно. Советы, полезные для решения некоторых частных задач, можно найти в электротехнических и математических справочниках.
Вполне удовлетворительный выход заключается в том, чтобы не делить переходный ток на две составляющие, а попытаться найти его как сумму результатов некоторых простых (элементарных) воздействий на цепь. При бесконечно большом числе элементарных воздействий сумма превращается в интеграл. Примером простого воздействия может служить включение цепи на единичное постоянное напряжение. В связи с этим возникает понятие переходной проводимости.
| И 1.30 | Переходная проводимость выбранной (k-ой) ветви пассивного двухполюсника равна переходному току, возникающему в этой ветви при включении двухполюсника на источник постоянного напряжения 1 вольт. |
Если цепь (двухполюсник) включается на постоянное напряжение u0, то переходная проводимость k-ой ветви

где  -переходный ток в этой ветви (рис. 1.21). Переходный ток пропорционален приложенному напряжению, поэтому при u 0 =1 переходная проводимость численно равна току. Как видно из последней формулы, размерность переходной проводимости – сименс(См).
-переходный ток в этой ветви (рис. 1.21). Переходный ток пропорционален приложенному напряжению, поэтому при u 0 =1 переходная проводимость численно равна току. Как видно из последней формулы, размерность переходной проводимости – сименс(См).
По аналогии с переходной проводимостью вводится понятие переходной функции по напряжению, которое используется для расчета напряжений на элементах цепи в течение переходного процесса.
Переходная функция по напряжению для любого элемента пассивного двухполюсника численно равна переходному напряжению, возникающему на этом элементе при включении двухполюсника на источник постоянного напряжения 1 вольт.
Если цепь включается на постоянное напряжение u 0, то переходная функция напряжения для n – го элемента равна

где 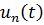 – переходное напряжение на этом элементе. Функция H(t) безразмерна.
– переходное напряжение на этом элементе. Функция H(t) безразмерна.
Пример 1.6. Определим переходную проводимость единственной ветви двухполюсника, показанного на рис. 1.22. После включения цепи в ней происходит переходный процесс, который описывается уравнением второго закона Кирхгофа

Установившийся ток равен  Начальное значение тока i (0)=0 по первому закону коммутации. Характеристическое уравнение
Начальное значение тока i (0)=0 по первому закону коммутации. Характеристическое уравнение  имеет корень
имеет корень  Переходный ток возрастает от нуля до установившегося значения по экспоненциальному закону (рис. 1.23., сплошная линия):
Переходный ток возрастает от нуля до установившегося значения по экспоненциальному закону (рис. 1.23., сплошная линия):

Коэффициент при экспоненте подобран так, чтобы выполнялось начальное условие i(0)=0.
Входная переходная проводимость двухполюсника по определению (39) равна

Пример 1.7. Определим переходные проводимости трех ветвей двухполюсника, представленного на рис. 1.24. Для упрощения расчетов допустим, что R 1 = R 2 = R 3 = R , u 0 =1.
Эквивалентное сопротивление цепи относительно зажимов источника  Установившиеся токи
Установившиеся токи  ,
,  . Начальные значения токов i 2 (0)=0 (по первому закону коммутации),
. Начальные значения токов i 2 (0)=0 (по первому закону коммутации),  (по законам Кирхгофа в момент коммутации). Характеристическое уравнение
(по законам Кирхгофа в момент коммутации). Характеристическое уравнение
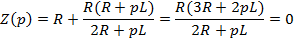
имеет корень  Переходные токи изменяются от начальных до установившихся значений по экспоненциальному закону (рис. 1.25). Переходные проводимости ветвей численно равны протекающим в них переходным токам:
Переходные токи изменяются от начальных до установившихся значений по экспоненциальному закону (рис. 1.25). Переходные проводимости ветвей численно равны протекающим в них переходным токам:


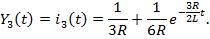
Коэффициенты при экспонентах подобраны так, чтобы при t=0 получались начальные значения токов.
Постоянные составляющие переходных проводимостей являются входной проводимостью первой ветви (  ) и передаточными проводимостями этой ветви (
) и передаточными проводимостями этой ветви (  ,
,  ) на постоянном токе (определение входной и передаточной проводимостей см. Часть 1, §2.3).
) на постоянном токе (определение входной и передаточной проводимостей см. Часть 1, §2.3).
До сих пор предполагалось, что отсчет времени начинается с момента коммутации, или включение цепи происходит в момент времени t =0. Когда цепь подвергается нескольким воздействиям и все они происходят в разные моменты времени, в решении задачи (в выражения переходных токов) входят моменты коммутации.
Допустим, что включение лабораторной катушки (рис. 1.22) произошло в момент времени τ>0. Переходный процесс будет происходить так же, как и при включении в момент t =0, но с запаздыванием на промежуток времени τ (рис. 1.23). В системе координат  кривая
кривая  выглядит так же, как кривая i ( t ) в системе координат ( t , i ). Значит, уравнения кривой i ( t ) в координатах ( t , i ) и кривой
выглядит так же, как кривая i ( t ) в системе координат ( t , i ). Значит, уравнения кривой i ( t ) в координатах ( t , i ) и кривой  в координатах
в координатах  одинаковы. Согласно уравнению (40)
одинаковы. Согласно уравнению (40)

По рис. 1.23 видно, что в любой точке оси ординат  , точнее,
, точнее,  (в частности,
(в частности,  при t =0 и
при t =0 и  при t=τ). Принимая во внимание зависимость между t и
при t=τ). Принимая во внимание зависимость между t и  , выражение (41) можно записать в виде
, выражение (41) можно записать в виде
 .
.
Это уравнение переходного тока для того случая, когда коммутация произведена с запаздыванием τ. Аргумент t-τ называется запаздывающим аргументом.
Переходные проводимости, как правило, записывают с запаздывающим аргументом, заменяя t на t -τ, например, в примере 1.6

Для каждого момента коммутации (если их несколько) получается свое значение запаздывания τ. Отсчет времени обычно начинается с момента первой коммутации.
Дата добавления: 2020-04-25; просмотров: 75; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
