Критерий устойчивости Рауса-Гурвица
Критерий устойчивости Гурвица — один из способов анализа линейной стационарной динамической системы на устойчивость, разработанный немецким математиком Адольфом Гурвицем. Наряду с критерием Рауса является представителем семейства алгебраических критериев устойчивости, в отличие от частотных критериев, таких как критерий устойчивости Найквиста. К достоинствам метода относятся простая реализация на ЭВМ, а к недостаткам — малая наглядность. Метод работает с коэффициентами характеристического уравнения системы. Пусть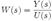 
— передаточная функция системы, а 
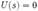— характеристическое уравнение системы. Представим характеристический полином 
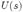в виде
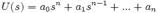Из коэффициентов характеристического уравнения строится определитель Гурвица 
по алгоритму: 1) по главной диагонали слева направо выставляются все коэффициенты характеристического уравнения от 
до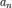 
2) от каждого элемента диагонали вверх и вниз достраиваются столбцы определителя так, чтобы индексы убывали сверху вниз; 3) на место коэффициентов с индексами меньше нуля или больше 
ставятся нули. Тогда согласно критерию Гурвица: Для того, чтобы динамическая система была устойчива, необходимо и достаточно, чтобы все 
диагональных миноров определителя Гурвица были положительны. Эти миноры называются определителями Гурвица. Пусть D(p) = a0pn + a1pn-1 + … + an, тогда:
|
|
|
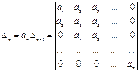- определитель Гурвица
Для того, чтобы система была устойчива необходимо и достаточно, чтобы ∆n и все его миноры были положительны при a0>0.
24) Принцип аргумента. Критерий устойчивости Михайлова
Принципом аргумента :Если функция f мероморфна в замыкании некоторой односвязной ограниченной области G с гладкой границей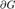 
и не имеет на её границе ни нулей, ни полюсов, то справедлива следующая формула: 
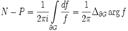где N и P — количества соответственно нулей и полюсов функции f в G, учтённых каждый с его кратностью, а 
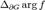— изменение аргумента f(z) при обходе вдоль контура области G (ориентацияконтура стандартная). Он является частотным критерием и позволяет судить об устойчивости замкнутой или разомкнутой системы по виду годографа характеристического вектора соответствующей системы.
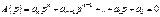
Перейдем к частотной функции характеристического многочлена, заменив p на jw:
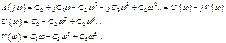
Критерий:
Для устойчивости линейной системы n-го порядка необходимо и достаточно, чтобы годограф Михайлова при изменении частоты в интервале от 0 до ∞, начинаясь в точке на вещественной положительной полуоси последовательно обходил против часовой стрелки n квадрантов комплексной плоскости, не пересекая начало координат.
|
|
|
2-я формулировка:
Для устойчивости линейной системы n-го порядка необходимо и достаточно, чтобы при изменении частоты от 0 до ∞ изменение фазы частотной функции характеристического уравнения: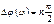 
Свойства чередования корней.
Для устойчивости системы корни должны чередоваться.
Дата добавления: 2020-04-25; просмотров: 128; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!