Вариационные ряды, их виды, методика построения. Обобщенная числовая характеристика изучаемого признака в вариационном ряду.
Для расчета средней величины необходимо построить вариационный ряд — т. е. ряд числовых измерений определенного признака, отличающихся по своей величине.
Вариационные ряды бывают следующих видов:
а) ранжированный, неранжированный;
б) сгруппированный, несгруппированный;
в) прерывный, непрерывный.
Ранжированный ряд — упорядоченный ряд; варианты располагаются последовательно по нарастанию или убыванию числовых значений.
Неранжированный ряд — варианты располагаются бессистемно.
Прерывный (дискретный) ряд — варианты выражены в виде целых (дискретных) чисел (окна в избе).
Непрерывный ряд – варианты могут быть выражены дробными числами.
Несгруппированный ряд – каждому значению варианты соответствует определенное число частот.
Сгруппированный ряд (интервальный) – варианты соединены в группы, объединяющие их по величине в пределах определенного интервала.
Ряд, в котором упорядоченно сопоставлены (по степени возрастания или убывания) варианты и соответствующие им частоты, называется вариационным. Отдельные числовые значения признака называются вариантами (У), а числа, показывающие, как часто эти варианты повторяются - частотами (Р), общее число наблюдений (n) равно сумме частот. Вариационный ряд может быть простым или сгруппированным. Простой вариационный ряд составляется при малом числе наблюдений (n<30), а сгруппированный - при большом числе наблюдений (n>30). Построение вариационного ряда из отдельных вариант - это только первый шаг к осмыслению особенностей всей совокупности. Далее для обобщенной числовой характеристики изучаемого признака у совокупности обследуемых рассчитываются средние величины, достоинство которых заключаются в том, что одна величина характеризует большую совокупность однородных явлений.
|
|
|
Средние величины, их виды. Методика вычисления. Стандарты физического развития, их использование для оценки здоровья детей и подростков.
Средняя величина - это число, выражающее общую меру исследуемого признака в совокупности. С помощью средних величин измеряют средний уровень изучаемого признака, т.е. то общее, что характерно для него в данной совокупности.
Применение средних величин
1. Для оценки состояния здоровья, например: средний рост, вес, функциональные показатели: АД, ЧСС, ЧД, уровень холестерина и.т.д.
2. при оценке организации медицинской помощи и деятельности ЛПУ, например средняя посещаемость в день, средняя длительность лечения по отдельным заболеваниям и.т.д.
Виды средних величин
a) Мода Мо - величина признака (или варианта), которая чаще других встречается в донной совокупности.
|
|
|
b) Медиана Ме – это величина признака, занимающая срединное положение в вариационном ряду. Она делит ряд на две равные по числу наблюдений части. Для ее определения находят середину ряда. В ряду с четным числом наблюдений за Ме принимают среднюю величину из двух центральных вариант. При нечетном числе наблюдений Ме будет соответствовать центральная варианта, для этого 
; где n- число наблюдений.
c) Средняя арифметическая М– это обобщенная величина, характеризующая размер варьирующего признака совокупности. Она равна среднему значению всех вариант в вариационном ряду.
Свойства средней арифметической:
-имеет абстрактный характер, не показывает индивидуальность, а характеризует то типичное, что свойственно всему ряду,
-занимает среднее положение в вариационном ряду,
-сумма отклонений всех вариант от средней арифметической равна нулю т.е.
S(V – M) = 0
Способы расчета средней арифметической
1. Среднеарифметический способ.
2. Способ моментов.
В зависимости от вида вариационного ряда используется тот или иной способ расчета средней. Средняя арифметическая для простого ряда, где каждая варианта встречается один раз, вычисляется по формуле: М = 
, где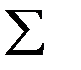 
- знак суммы, V –отдельные значения вариант, n –число наблюдений. Средняя арифметическая взвешенная определяется по формуле: М= 
, где 
- знак суммы, V –отдельные значения вариант, n –число наблюдений, р – частота встречаемости вариант. Одним из наиболее простых и достаточно точных способов расчета средней арифметической является способ моментов, основанный на том, что алгебраическая сумма отклонений каждой варианты вариационного ряда от средней арифметической равна нулю. М= А + i 
, где А – условно принятая средняя или мода, а - отклонение каждой варианты от условно принятой средней, р –частота встречаемости вариант, n –число наблюдений, i – интервал или расстояние между соседними вариантами. Основные свойства средней величины: 1) имеет абстрактный характер, так как является обобщающей величиной: в ней стираются случайные колебания; 2) занимает срединное положение в ряду (в строго симметричном ряду); 3) сумма отклонений всех вариант от средней величины равна нулю. Данное свойство средней величины используется для проверки правильности расчета средней. Она оценивается по уровню колеблемости вариационного ряда. Критериями такой оценки могут служить: амплитуда (разница между крайними вариантами); среднее квадратическое отклонение, показывающее, как отличаются варианты от рассчитанной средней величины; коэффициент вариации.
|
|
|
Среднеквадратическое отклонение ( 
) наиболее точно характеризует степень разнообразия варьирующего признака, без чего нельзя достаточно полно охарактеризовать явление. Для простого вариационного ряда (р =1) среднеквадратическое отклонение расчитывается по формуле 
. Для взвешенного вариационного ряда по формуле:
|
|
|
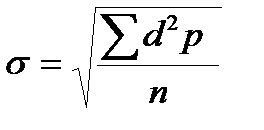, где d = V – M - отклонение каждой варианты от средней арифметической. При числе наблюдений меньше 30 в знаменателе этих формул берется не n, а n – 1 (так называемое в статистике число степеней свободы). При числе наблюдений более 30 уменьшение знаменателя на единицу не имеет практического значения, т.к. существенно не сказывается на конечном результате. Значительно упрощает вычисления расчет среднего квадратического отклонения по способу моментов.
где, величина 
называется моментом первой степени, а 
- моментом второй степени.
Степень разнообразия (колеблемости) признака в вариационном ряду можно оценить по коэффициенту вариации (отношение среднего квадратического отклонения к средней величине, умноженное на 100%); при вариации менее 10% отмечается слабое разнообразие, при вариации 10—20% — среднее, а при вариации более 20% — сильное разнообразие признака. Если нет возможности сравнить вариационный ряд с другими, то используют правило трех сигм. Если к средней прибавить одну сигму, то этой вычисленной средней соответствует 68,3%, при двух сигмах — 95,4%, при трех сигмах — 99,7% от всех признаков. В медицине с величиной М ± 1σ связано понятие нормы; отклонения от средней (в любую сторону) больше, чем на 1σ, но меньше чем на 2σ, считаются субнормальными (выше или ниже нормы), а при отклонении от средней больше чем на 2σ, варианты считаются значительно отличающимися от нормы (патология).
Мерой точности и достоверности результатов выборочных статистических величин являются средние ошибки представительности (репрезентативности). Средняя ошибка средней арифметической – m (отношение среднего квадратического отклонения к квадратному корню из общего числа наблюдений — объектов). m =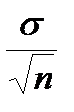 
Мерой достоверности среднего показателя наряду с его ошибкой являются, доверительные границы и достоверность разности между двумя средними величинами.
Термин «физическое развитие», с одной стороны, обозначает процесс формирования и созревания детского организма, с другой – степень этого созревания на каждом данном отрезке времени, т. е. имеет, как минимум, два значения. Исходя из этого под физическим развитием понимают совокупность морфологических, функциональных свойств и качеств, а также уровень биологического развития (биологический возраст) организма, характеризующий процесс созревания ребенка на определенном этапе жизни.
Соматометрия включает определение длины, массы тела, окружности грудной клетки.
тобы полученные данные были приняты за стандарт, они должны отвечать определенным требованиям.
1. Стандарты физического развития должны быть региональными.
2. Статистическая совокупность должна быть репрезентативна, поэтому каждая возрастно-половая группа должна быть представлена не менее чем 100 детьми (единицами наблюдения).
3. Статистическая совокупность должна быть однородна по полу, возрасту (с учетом гетероморфности, гетерохронности и полового диморфизма физического развития), этнической принадлежности (так как в физическом развитии народностей и наций имеются значимые различия), месту проживания (из-за возможного влияния биогеохимических провинций на физическое развитие) и состоянию здоровья.
4. Из группы наблюдения должны быть исключены все случаи «неоднородности» по состоянию здоровья: дети, имеющие хронические заболевания, протекающие с интоксикацией (туберкулез, ревматизм и т. д.), серьезные нарушения в деятельности органов и систем организма (врожденные пороки сердца, последствия полиомиелита, костного туберкулеза, травм нервной системы и опорно-двигательного аппарата и т. д.), эндокринные заболевания. При разработке материалов обследования детей раннего возраста исключают детей с выраженным рахитом, гипотрофией, недоношенных, двойни.
5. После формирования однородной и репрезентативной статистической совокупности должна применяться единая методика обследования, измерения, обработки и анализа данных.
Общепринятых стандартов физического развития не существует. Различные условия жизни в разных климато-географических зонах, в городах и сельской местности, этнографические различия обуславливают разный уровень физического развития детского населения. Кроме того, учитывая изменения показателей физического развития в динамике лет (акселерация и децелерация физического развития), региональные стандарты должны уточняться каждые 5—10 лет.
Дата добавления: 2020-04-25; просмотров: 1018; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!