Относительные величины, их виды, методика расчета. Применение в статистике и работе педиатра.
ОТНОСИТЕЛЬНЫЕ ВЕЛИЧИНЫ Применение: 1. Для определение частоты, уровня, распространенности явления, 2. Для сравнения различных совокупностей по степени частоты явления (заболеваемости, смертности). 3. Выявление в динамике изменений в частоте явления (рождаемость за ряд лет). Графическое изображение: 1. столбиковая диаграмма – иллюстрирует однородные, но не связанные между собой явления, изображает статику явления; 2. ленточная диаграмма – разновидность столбиковой, 3. линейная диаграмма – отражает изменение явления во времени; 4. радиальная диаграмма – разновидность линейной, используется для демонстрации явления, имеющего замкнутый цикл; 5. картограмма – карта территории на которой разным цветом или разной интенсивностью одного цвета показана распространенность явления. 6. картодиаграмма – сочетание карты и диаграммы, в котором распространенность явления на определенной территории показана разной высотой столбиков (имеет трехмерный и масштабный вид). Относительные величины бывают четырех видов: интенсивные, экстенсивные, показатели соотношения, показатели наглядности. Интенсивные показатели - показывают частоту явления в среде. В качестве среды обычно выступает некая совокупность объектов (населения, пациентов, случаев), у части которых происходит какое-то явление. Рассчитывается по следующей формуле: И.п. = явление/среда*коэффициент. Коэффициент используется для удобства представления показателя, представляет собой различные степени числа 10 и обычно принимает значения 100, 1000, 10 000, 100 000. Его величина зависит от частоты встречаемости явления: чем реже встречается, тем больше коэффициент. Так, показатели рождаемости, смертности, общей заболеваемости населения обычно рассчитываются на 1000 человек. При расчете материнской смертности, как значительно более редкого события, используется коэффициент 100 000. Наоборот, частота такого распространенного явления, как случай временной утраты трудоспособности, рассчитывается на 100 работающих. Пример расчета интенсивного показателя: За год в больнице Н. было выполнено 360 хирургических операций. В 54 случаях в послеоперационном периоде наблюдались различные осложнения. Найти частоту послеоперационных осложнений из расчета на 100 операций. Решение: Частота послеоперационных осложнений - это интенсивный показатель, который может быть рассчитан как отношение явления к среде. Средой выступает совокупность выполненных операций (360), из числа которых в 54 случаях, как следует из условия задачи, происходило явление - отмечались послеоперационные осложнения. Таким образом: Частота послеоперационных осложнений = (Число случаев послеоперационных осложнений) / (Число выполненных операций) * 100 = (54 / 360) * 100 = 15.
|
|
|
Значение коэффициента принято равным 100, так как в условии задачи спрашивается частота, рассчитанная на 100 выполненных операций. Ответ: Частота послеоперационных осложнений в больнице Н. за год составила 15 случаев на 100 выполненных операций. Экстенсивные показатели - характеризуют структуру явления, измеряются в процентах, реже - в промилле или долях единицы. Экстенсивные величины показывают, какую часть составляет отдельная группа единиц в структуре всей совокупности. Рассчитываются по формуле: Э.п. = часть/целое*100%. Пример расчета экстенсивного показателя: В исследовании эффективности лечения пневмонии с использованием нового антибиотика приняли участие 200 пациентов, из них 90 - мужчины. Необходимо определить долю мужчин среди исследуемых, результат выразить в %. Решение: Пациенты мужского пола представляют собой часть от всей совокупности исследуемых. Следовательно, мы должны воспользоваться формулой для расчета экстенсивных показателей: Доля пациентов мужского пола среди всех исследуемых = (число мужчин) / (число всех пациентов) * 100% = (90 / 200) * 100% = 45%. Ответ: Доля пациентов в структуре исследуемых составляет 45%.
|
|
|
Показатели соотношения - характеризуют отношение двух не связанных между собой совокупностей. Данные совокупности могут измеряться в одних величинах, главное условие, что их изменения должны происходить независимо друг от друга. Обычно в таком виде представляются различные индексы, коэффициенты, показатели обеспеченности населения. Рассчитываются по следующей формуле: П.с. = (первая совокупность) / (вторая совокупность)*коэффициент Коэффициент обычно принимает значения 1 (для индексов) или 10 000 (для показателей обеспеченности населения). Пример расчета показателя соотношения: В одном из районов Республики Татарстан проживает 40 000 населения. В лечебнопрофилактических учреждениях данного района развернуты 384 стационарные койки. Какова обеспеченность населения койками в районе? Решение:Мы имеем две совокупности: население и стационарные койки. Изменения числа населения не зависят от изменений числа стационарных коек и наоборот, в связи с чем делаем вывод о том, что представленные совокупности не связаны между собой. Рассчитаем показатель обеспеченности населения стационарными койками: Обеспеченность населения койками = (число коек) / (численность населения) *10 000 = (384 / 40 000) * 10 000 = 96. Ответ: Обеспеченность населения стационарными койками составляет 96 на 10 000 населения. Показатели наглядности – относительная величина, указывающая на соотношение однородных показателей для разных групп или разных периодов, вычисляемая путем принятия одной из сравниваемых величин за 100 или (реже) за 1000, 10 000 и т. п. П.Н. = (показатель текущего года) : (показатель базового года) *100%
|
|
|
|
|
|
Виды относительных величин и их применение в практической работе врача: Относительная величина - это обобщающий показатель, который дает числовую меру соотношения двух сопоставляемых абсолютных величин. Встречаются при проведении статистического анализа. Виды: интенсивный, экстенсивный показатели, показатель наглядности и соотношения. а) относительные величины, выражающие распространённость, частоту явления в среде Интенсивные показатели – отражают частоту встречаемости явления в среде.
k – основание, коэффициент, обычно принимает значение 100, 1000, 10 000, 100 000 (чем реже явление, тем больше основание) Примеры: рождаемость, смертность, заболеваемость б) относительные величины, выражающие долю явления, его удельный вес Экстенсивные показатели – характеризуют распределение целого на составляющие его части по их удельному весу, т.е. раскрывают внутреннюю структуру изучаемого явления.
Примеры: структура смертности, структура заболеваемости в) с помощью каких графических изображений лучше выразить структуру какого-либо явления? Секторные (круговые) и внутристолбиковые диаграммы.
с учебника!!!!!!!!!!!!!!!!!!!!!
В санитарной статистике используют следующие виды относительных величин: экстенсивные коэффициенты; интенсивные коэффициенты; коэффициенты соотношения; коэффициенты наглядности.
Экстенсивные коэффициенты характеризуют отношение части к целому, то есть определяют долю (удельный вес), процент части в целом, принятом за 100%. Используются для характеристики структуры статистической совокупности. Например: удельный вес (доля) заболеваний гриппом среди всех заболеваний в процентах; доля производственных травм среди всех травм у рабочих (отношение числа производственных травм к общему числу травм, умноженное на 100%). Вычисление экстенсивного показателя производится по формуле:
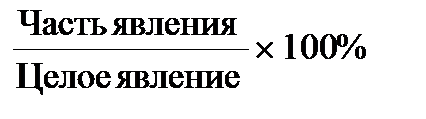
Интенсивные коэффициенты отражают частоту (уровень, распространенность) явления в однородной среде. На практике их применяют для оценки здоровья населения, медико-демографических процессов. Например: число случаев заболеваний с временной утратой трудоспособности на 100 работающих; число заболевших гипертонической болезнью на 1000 жителей; число родившихся на 1000 человек (определяется как отношение числа родившихся за год к средней численности населения административной территории, умноженное на 1000). Вычисление интенсивного показателя производится по формуле:
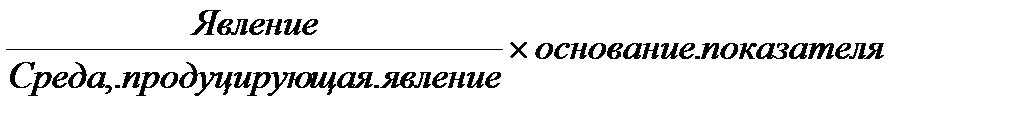
В медико-социальных исследованиях за «среду», как правило, принимается численность населения в целом, а также отдельных его групп (по возрасту, полу, профессии, месту жительства и т.д.). Явление представляет собой как бы продукт «среды». Например: число заболевших, родившихся детей, инвалидов. Основание – единица с нулями: 100, 1000, 10000, 100000 человек. В результате полученные данные выражаются в процентах (%), промилле (‰), продецимилле (%00), просантимилле (%000)
Интенсивные коэффициенты бывают общие и специальные. При расчете общих интенсивных показателей за среду принимается численность населения в целом (показатель рождаемости, общий показатель смертности, показатель заболеваемости и др.). Специальные – вычисляют для отдельных групп населения: показатель плодовитости изучает число детей, родившихся на 1000 женщин детородного возраста, уровень заболеваемости гипертонической болезнью женщин-педагогов, повозрастной показатель смертности - число умерших в определенном возрасте и др.
Коэффициенты соотношения (показатель частоты, распространенности явления в разнородных средах) характеризуют численное соотношение двух не связанных между собой, самостоятельных совокупностей. Методика расчета показателей соотношения сходна с методикой вычисления интенсивных показателей, хотя они различны по существу.
Показатель соотношения = 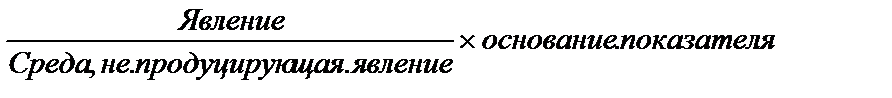
Показатели соотношения используются для характеристики обеспеченности уровня и качества медицинской помощью: число коек на 10000 человек; число врачей на 10000 жителей; число лекарственных препаратов, произведенных на 1000 жителей (отношение числа выпущенных лекарственных препаратов, к численности населения административной территории, умноженное на 1000).
Показатель наглядности применяется с целью более наглядного и доступного сравнения рядов абсолютных, относительных и средних величин. Коэффициент наглядности определяет, на сколько процентов или во сколько раз произошло увеличение или уменьшение сравниваемых величин. Используется для характеристики динамики явления. При вычислении показателей наглядности одна из сравниваемых величин принимается за 100% или за единицу, а остальные величины с помощью пропорции пересчитываются в коэффициенты по отношению к этому числу. Чаще всего за 100% принимается первая исходная величина, но за 100 может быть принята величина и из середины, конца ряда. Например, число врачей в 2005 г. по сравнению с числом врачей в 2006 г., принятым за 100% (отношение числа специалистов в данном году к числу специалистов в предыдущем году, умноженное на 100%).
Дата добавления: 2020-04-25; просмотров: 342; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
