Естественные координатные оси
Точка перемещается в пространстве по заданному уравнению движения S = f(t) (рис. 2.12).
Проведём в точке М кривой АВ соприкасающуюся плоскость, нормальную плоскость, перпендикулярную соприкасающейся плоскости, и спрямляющую плоскость, перпендикулярную соприкасающейся и нормальной плоскостям. Пересечением трёх плоскостей образован естественный трёхгранник.
Линию пересечения соприкасающейся и нормальной плоскостей называют главной нормалью.
Линию пересечения спрямляющей и соприкасающейся плоскостей называют касательной.
Линию пересечения спрямляющей и нормальной плоскостей называют бинормалью.
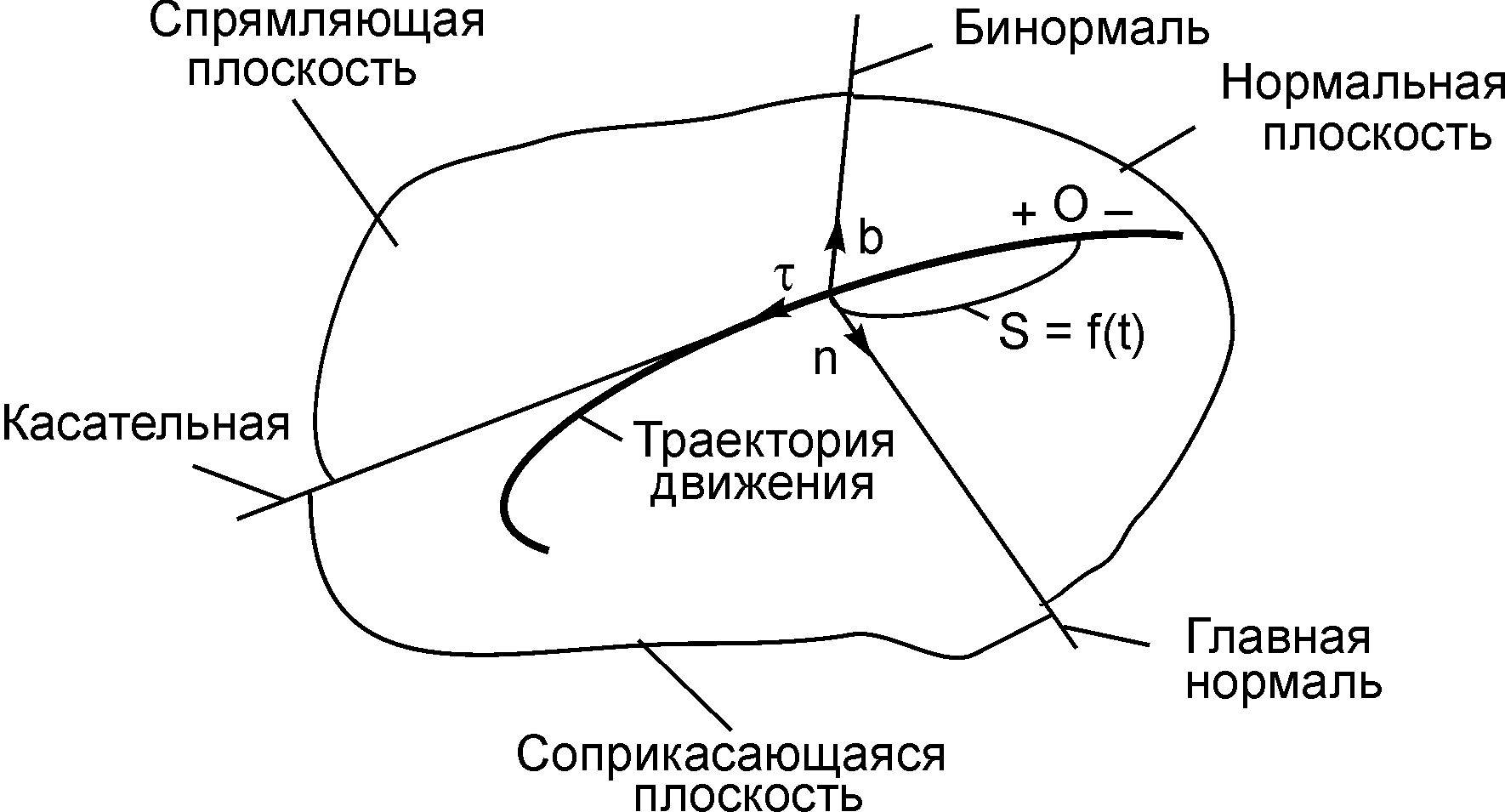Рис. 2.12
|
Естественными координатными осями называют три взаимно перпендикулярные оси: касательная (единичный вектор τ всегда направлен в сторону возрастания дуговой координаты S); главная нормаль (единичный вектор n направлен в сторону вогнутости траектории); бинормаль (единичный вектор b перпендикулярен векторам τиnи направлен так же, как и вектор k по отношению к векторам i, j в правой декартовой системе отсчёта OXYZ) (рис. 2.13).
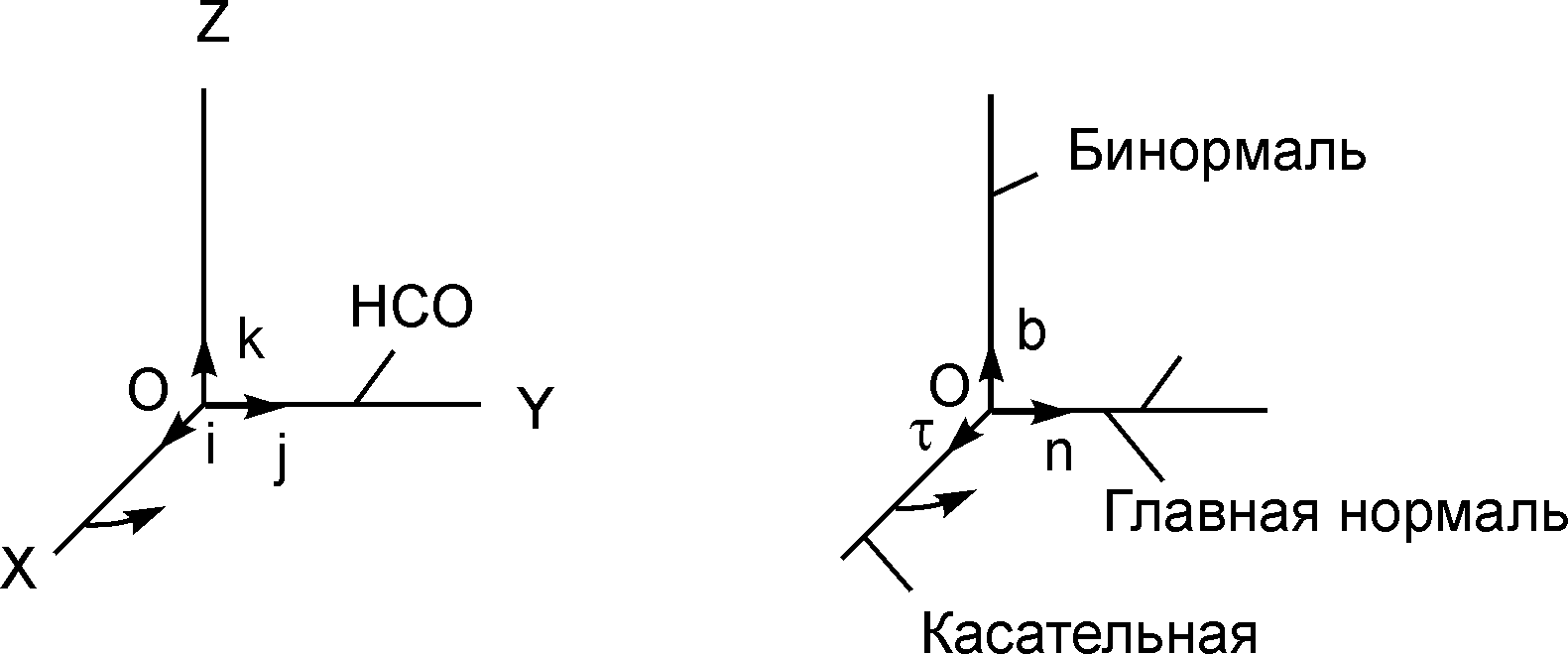Рис. 2.13
|
Если в правой системе отсчёта OXYZ смотреть на единичные векторы I, jс положительного направления оси OZ (навстречу вектору k), то для совпадения направлений векторов i, j вектор iнеобходимо поворачивать против хода часовой стрелки. По такому же правилу ориентируются в пространстве векторы τ, n, b.
|
|
|
Начало естественных координатных осей всегда располагается в точке (см. рис. 2.12) и при движении по траектории перемещается вместе с ней. Естественные координатные оси, оставаясь взаимно перпендикулярными, изменяют своё направление в пространстве. Следовательно, естественные координатные оси образуют подвижную систему отсчёта (ПСО).
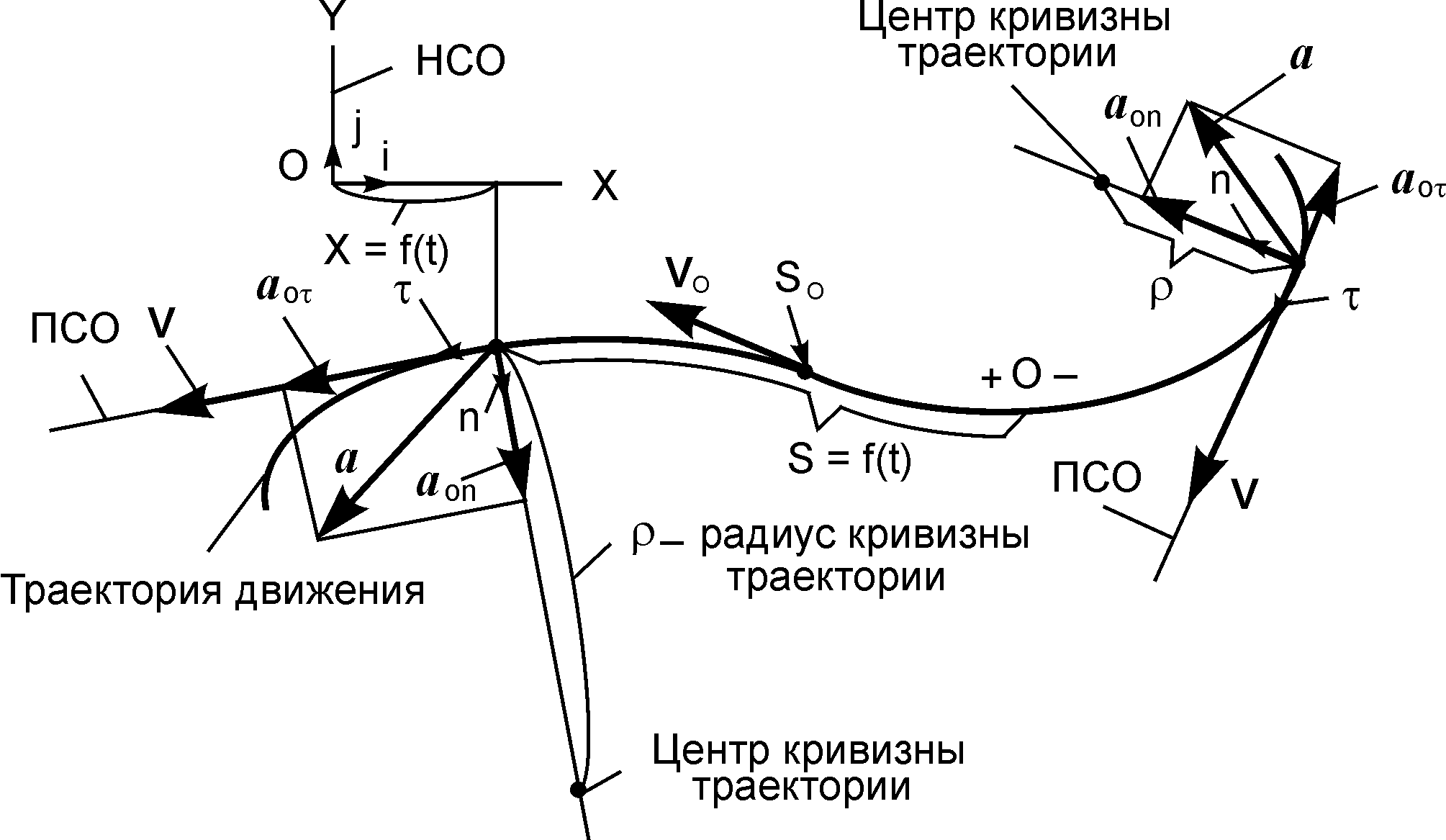Рис. 2.14
|
Рассмотрим движение точки на плоскости OXY (рис. 2.14).
На рис. 2.14 орты τи n расположены в соприкасающейся плоскости, а орт b не виден, так как он перпендикулярен ортам τи n и плоскости рисунка.
Главная нормаль всегда проходит через центр кривизны траектории движения точки. Здесь ρ – радиус кривизны траектории движения. При движении точки по окружности радиусом R радиус кривизны траектории ρ = R. При движении точки по прямой линии ρ =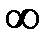 
. В остальных случаях при движении точки по криволинейной траектории радиус её кривизны является переменной величиной.
Скорость точки
Скорость точки при естественном способе задания движения определяется по формуле
V = τ·(dS/dt) = τ·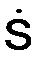 
,
где dS/dt = 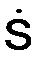– проекция скорости V на касательную.
Символ (·) означает однократное дифференцирование функции S = f(t) по времени.
|
|
|
Таким образом, проекция скорости на касательную равна первой производной по времени от уравнения движения S = f ( t ).
В данном учебно-методическом пособии проекцию скорости V на касательную принято обозначать .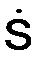
Как известно, вектор Vскорости точки всегда направлен по касательной к траектории движения.
Проекция скорости на касательную может быть положительной, отрицательной и равной нулю.
Если в некоторый момент времени 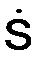> 0, то в этот момент функция S = f(t) возрастает, т. е. точка движется в сторону увеличения дуговой координаты S и направление вектора скорости Vсовпадает с направлением орта τ(см. рис. 2.14).
Если 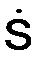< 0, то в этот момент времени функция S убывает и, следовательно, направление скорости Vпротивоположно направлению орта τ.
Если, непрерывно изменяясь, 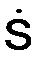при переходе через значение 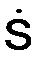= 0 изменяет знак, то дуговая координата S достигает максимума или минимума, т. е. изменяется направление движения точки.
Модуль скорости V находят по формуле V = | |.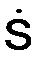
Ускорение точки
Ускорение а точки всегда направлено в сторону вогнутости траектории движения, лежит в соприкасающейся плоскости (см. рис. 2.14) и находится по формуле
|
|
|
a= аoτ+ аon,
где аoτ–касательное ускорение; аon – нормальное ускорение.
Ускорение точки равно геометрической сумме двух векторов, один из которых направлен по главной нормали и называется нормальным ускорением, а другой направлен по касательной и называется касательным ускорением.
Касательное аoτ и нормальное аon ускорения называют также компонентами ускорения по естественным координатным осям.
Касательное ускорение аoτхарактеризует быстроту изменения величины скорости V и находится по формуле
аoτ=τ ·(d2S/dt2) = τ ·(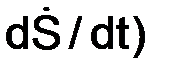 
= τ· 
,
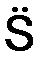где 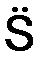= d2S/dt2 = 
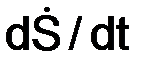– проекция ускорения aточки на касательную.
Таким образом, проекция ускорения точки на касательную равна второй производной по времени от дуговой координаты S = f ( t ) или первой производной по времени от проекции скорости на касательную.
Символ (··) означает двойное дифференцирование функции S = f(t) по времени.
Из приведённых обозначений проекций ускорения на касательную, как правило, используют обозначение .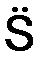
Эта проекция ( 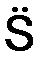) имеет знак (+), если направления касательного ускорения аoτи орта τсовпадают, и знак (–), если они противоположны по направлениям.
Касательное ускорение аoτ характеризует быстроту изменения величины скорости.
|
|
|
Нормальное ускорение аon характеризует быстроту изменения направления скорости и находится по формуле
аon = n·(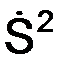 
/ρ).
Так как 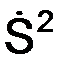/ρ> 0, то нормальное ускорение всегда совпадает с направлением орта n, т. е. всегда направлено к центру кривизны траектории движения точки.
При прямолинейном движении точки радиус кривизны траектории движения ρ =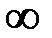 
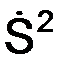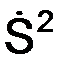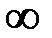и, следовательно, аon = /ρ = / = 0.
Таким образом, нормальное ускорение существует только при криволинейном движении.
В случае естественного способа задания движения, когда известна траектория точки, а, следовательно, её радиус кривизны ρ в любой точке и уравнение движения S = f(t), можно найти проекции ускорения точки на естественные координатные оси и по ним определить модуль и направление ускорения по формулам:
a=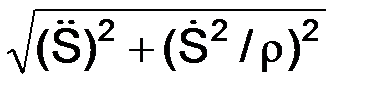 
;
cos(а , i) = 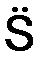/a; cos(а , n) = ( 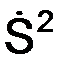/ρ)/a.
Модули скорости и ускорения точки при естественном и координатном способах задания движения точки связаны следующими зависимостями:
V = | | =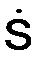 
;
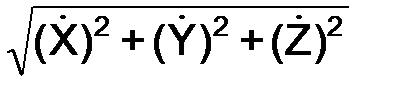a = =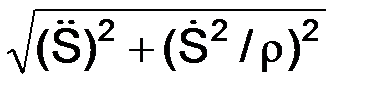 
;
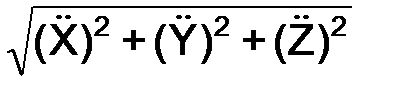аoτ = |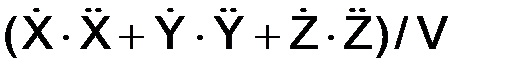 
|.
Классификация движения точки
По ускорениям её движения
Случай 1: аon= 0; аoτ = 0 – точка движется равномерно и прямолинейно.
Случай 2: аon ≠ 0; аoτ = 0 = const – точка движется равномерно по криволинейной траектории.
Случай 3: аon = 0; аoτ ≠ 0 – точка движется не равномерно по прямой линии.
Случай 4: аon≠ 0; аoτ ≠ 0 – точка совершает неравномерное криволинейное движение.
Случай 5: если, непрерывно изменяясь, в некоторый момент времени аoτ = 0, то в этот момент скорость V достигает экстремального значения.
Дата добавления: 2020-04-25; просмотров: 203; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!