Решение задачи модифицированным методом Фурье.
Федеральное агенство по рыболовству
Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Мурманский Государственный Технический Университет»
| Оценка: ________________ «___» ____________ 2009 г. | Кафедра Высшей математики и программного обеспечения ЭВМ |
Пояснительная записка к курсовой работе
«Решение краевой задачи для одного из уравнений математической физики»
по дисциплине «Специальные разделы высшей математики»
Выполнил:
студент группы П-281
Е.Л. Куликов
Проверил:
доцент кафедры
ВМ и ПО ЭВМ
В. С. Кацуба
Мурманск, 2009
Оглавление
§1. Условие физической задачи. 3
§2. Вывод уравнения состояния (уравнение Лапласа)[2] 4
§3. Формулировка математической модели задачи. 6
§4. Решение задачи модифицированным методом Фурье. 7
§5. Доказательство достоверности решения, полученного методом Фурье. 14
|
|
|
§6. Табулирование значений искомой функции в узлах сетки, покрывающей область, ____в которой найдено решение. 16
§7. Вывод конечно-разностных уравнений, формулировка вычислительной схемы ___метода конечных разностей. 19
§8.Исследование решения задачи. 22
§9. Анализ результатов решения задачи. 26
§10. Список использованной литературы и ПО.. 27
Приложение 1. График функции  ........... 27
........... 27
Приложение 2. График функции  ........... 29
........... 29
Условие физической задачи
Найти распределение электростатического потенциала  в заданной области
в заданной области
D:  , если известна информация о функции
, если известна информация о функции  на границе области D:
на границе области D:
 .
.
Задание на исследование решения:
1.Построить линии уровня функции  для значений параметров
для значений параметров  и
и  таких, что
таких, что

2.По плотности расположения линий уровня по области  сделать вывод об интенсивности изменения электростатического потенциала по области
сделать вывод об интенсивности изменения электростатического потенциала по области  .
.
§ 2. Вывод уравнения состояния (уравнение Лапласа)[2]
Пусть в однородной среде, заполняющей некоторый объем V, проходит электрический ток, плотность которого в каждой точке  задается векторной функцией
задается векторной функцией

Предположим, что плотность тока не зависит от времени  . Предположим далее, что в рассматриваемом объеме нет источников тока. Следовательно, поток вектора
. Предположим далее, что в рассматриваемом объеме нет источников тока. Следовательно, поток вектора 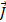 через любую замкнутую поверхность
через любую замкнутую поверхность 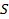 , лежащую внутри объема
, лежащую внутри объема  , будет равен нулю:
, будет равен нулю:
|
|
|

где  – единичный вектор, направленный по внешней нормали к поверхности
– единичный вектор, направленный по внешней нормали к поверхности 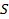 . Преобразуем по формуле Остроградского-Гаусса интеграл по замкнутой поверхности к тройному интегралу по объему, ограниченному этой поверхностью. В результате получим, что
. Преобразуем по формуле Остроградского-Гаусса интеграл по замкнутой поверхности к тройному интегралу по объему, ограниченному этой поверхностью. В результате получим, что

Теорема о среднем в интегральном исчислении позволяет сделать следующий важный вывод: если интеграл от непрерывной функции по любому геометрическому объекту интегрирования равен 0, то это означает, что равна нулю подынтегральная функция во всех точках этого геометрического объекта. Следовательно, последнее равенство дает, что:

На основании обобщенного закона Ома определяем в рассматриваемой проводящей среде электрическую силу (напряженность электростатического поля):
 , или
, или  ,
, 
где λ – проводимость среды, которую мы будем считать постоянной.
Из общих уравнений электромагнитного поля (уравнения Максвелла) следует, что если процесс стационарный, то векторное поле  безвихревое, т.е.
безвихревое, т.е.  . Тогда это поле является потенциальным, следовательно, существует функция φ такая, что:
. Тогда это поле является потенциальным, следовательно, существует функция φ такая, что:
|
|
|

Функция  называется потенциалом векторного поля
называется потенциалом векторного поля  . На основании (*) получаем:
. На основании (*) получаем:

Теперь уравнение  приводится к виду:
приводится к виду:
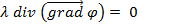
Из определений дивергенции и градиента имеем, что:
 , или
, или 
Получили трехмерное уравнение Лапласа, которому удовлетворяет функция  – потенциал электростатического поля.
– потенциал электростатического поля.
Поскольку в данной задаче мы имеем дело с электростатическим потенциалом в двухмерной области, то уравнение Лапласа будет двумерным и имеет вид:
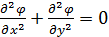 .
.
Если исходить из данного условия задачи для решения в курсовой работе, то функцию  нужно переобозначить на U(x,y). Тогда дифференциальное уравнение состояния для процесса в поставленной задаче имеет вид:
нужно переобозначить на U(x,y). Тогда дифференциальное уравнение состояния для процесса в поставленной задаче имеет вид:
 .
.
§3. Формулировка математической модели задачи.
y

b


D
0  a x
a x
Имеем ДУЧП Лапласа: 
Требуется найти функцию U(x,y), где  , удовлетворяющую граничным условиям Неймана и условиям Дирихле:
, удовлетворяющую граничным условиям Неймана и условиям Дирихле:
|
|
|

На границе области D поддерживается заданный электростатический потенциал: на участках границы  потенциал равен 0 (участки электроизолированы), а на участках
потенциал равен 0 (участки электроизолированы), а на участках  и
и  задаются значения
задаются значения  известными функциями
известными функциями 
Функция  – величина электростатического потенциала в точке
– величина электростатического потенциала в точке  этой области D.
этой области D.
Данная задача представляет собой смешанную краевую задачу для ДУЧП эллиптического типа.
Необходимые условия для решения задачи методом Фурье выполнены не полностью (а именно – нет равенства нулю граничных условий на 2-х противоположных сторонах прямоугольной области), поэтому дальнейшее решение продолжаем по модифицированному методу Фурье.
Управляемые параметры в задаче:  – длины сторон прямоугольной области D,
– длины сторон прямоугольной области D,
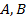 – константы из функций, задающих граничные условия.
– константы из функций, задающих граничные условия.
Решение задачи модифицированным методом Фурье.
Для ДУЧП Лапласа имеем: 
Представим искомую функцию  в виде суммы 2-х функций:
в виде суммы 2-х функций:

Где для каждой функции 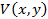 и
и 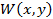 поставим краевую задачу с нулевыми граничными условиями на двух противоположных сторонах прямоугольной области.
поставим краевую задачу с нулевыми граничными условиями на двух противоположных сторонах прямоугольной области.
Для 
y

b

D
0  a x
a x


Для 
y

b


D
0  a x
a x


I.Найдем функцию 
Будем находить функцию  подбором как какую-нибудь функцию, удовлетворяющую всем поставленным на нее условиям:
подбором как какую-нибудь функцию, удовлетворяющую всем поставленным на нее условиям:

Находим функцию  подбором:
подбором:
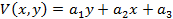 – линейная функция по x и y.
– линейная функция по x и y.
Эта функция, очевидно, удовлетворяет ДУЧП:

Коэффициенты a1 a2, a3 попробуем подобрать так, чтобы удовлетворялись граничные условия:

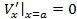 – верно, если a2=0;
– верно, если a2=0;


Получаем, что 
Проверка:
 ;
;  ;
; 
 подбором получена функция
подбором получена функция  , удовлетворяющая ДУЧП и поставленным граничным условиям.
, удовлетворяющая ДУЧП и поставленным граничным условиям.
II.Найдем функцию  классическим методом Фурье
классическим методом Фурье
1. Искомую функцию  двух переменных ищем в виде произведения 2-х функций, каждая из которых зависит только от одной переменной:
двух переменных ищем в виде произведения 2-х функций, каждая из которых зависит только от одной переменной:

Далее разделяем переменные в ДУЧП:

Где  - это постоянная величина и по переменной
- это постоянная величина и по переменной  , и по переменной
, и по переменной  .
.
Получаем систему двух обыкновенных дифференциальных уравнений:

2. Перебрасываем нулевые граничные условия:

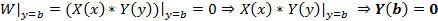
3. Решаем задачу Штурма — Лиувилля для второго уравнения системы (8) вместе с условиями (9)

т.е. найдем собственные числа  , при которых система имеет нетривиальные решения в виде собственных функций
, при которых система имеет нетривиальные решения в виде собственных функций  .
.
ДУ из системы (10):  – ДУ второго порядка относительно функции
– ДУ второго порядка относительно функции  , линейное, однородное с постоянными коэффициентами, поэтому
, линейное, однородное с постоянными коэффициентами, поэтому
 где
где  – константы,
– константы,
 – ФСЧР, которая находится с помощью корней характеристического уравнения.
– ФСЧР, которая находится с помощью корней характеристического уравнения.
Характеристическое уравнение имеет вид: 
В случае 
 - действительные различные корни, причем
- действительные различные корни, причем 

ФСЧР: 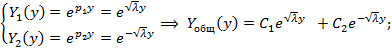
Подставляем граничные условия:


таким образом, в случае  система (10) имеет только тривиальное решение
система (10) имеет только тривиальное решение 
В случае 
 - действительные равные корни,
- действительные равные корни, 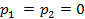
ФСЧР: 
Подставляем граничные условия:


таким образом в случае  система (10) также имеет только тривиальное решение.
система (10) также имеет только тривиальное решение.
В случае 
 – случай комплексно-сопряженных корней с
– случай комплексно-сопряженных корней с 
ФСЧР: 
Подставляем граничные условия:





Таким образом, в данной краевой задаче задача Штурма-Лиувилля оказалась разрешимой при  , и в результате получилось следующее счетное множество собственных чисел и собственных функций:
, и в результате получилось следующее счетное множество собственных чисел и собственных функций:

4. Решаем первое ДУ из системы (8):  ,
,
где числа  известны уже по формулам (11);
известны уже по формулам (11);
это обыкновенное ДУ 2-го порядка относительно функции  , линейное, однородное с постоянными коэффициентами, поэтому
, линейное, однородное с постоянными коэффициентами, поэтому
 где
где  – константы,
– константы,  – ФСЧР;
– ФСЧР;
находим ФСЧР через корни характеристического уравнения:

 - действительные различные корни;
- действительные различные корни;
ФСЧР : 
Для дальнейшего решения в задаче для ДУЧП Лапласа удобно перейти к другой фундаментальной системе: 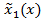 и
и  по формулам:
по формулам:


Тогда имеем:


5. Перемножим функции  и
и  и получаем счетное множество функций
и получаем счетное множество функций  , каждая из которых удовлетворяет исходному ДУЧП и нулевым граничным условиям на 2-х противоположных сторонах прямоугольной области.
, каждая из которых удовлетворяет исходному ДУЧП и нулевым граничным условиям на 2-х противоположных сторонах прямоугольной области.
Переобозначим произвольные пока коэффициенты: 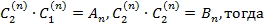

Чтобы удовлетворить оставшимся двум условиям из набора (5) для  составим ряд из всех этих функций
составим ряд из всех этих функций  , предположим, что он сходится равномерно внутри области D, и его сумму обозначим как
, предположим, что он сходится равномерно внутри области D, и его сумму обозначим как  . Отсюда получится:
. Отсюда получится:
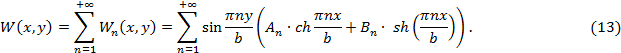
6. Находим коэффициенты 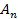 и
и  , удовлетворяя функцией (13) граничным условиям при
, удовлетворяя функцией (13) граничным условиям при  и
и  .
.

Граничные условия:
t wx:val="Cambria Math"/><w:i/></w:rPr><m:t>n</m:t></m:r></m:sub></m:sSub></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 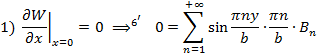
Получилось разложение в ряд Фурье по синусам функции  , дополненной нечетным образом на промежуток
, дополненной нечетным образом на промежуток  и продолженной на всю числовую ось периодически с
и продолженной на всю числовую ось периодически с  , значит, для нахождения коэффициентов этого ряда можно использовать стандартные формулы Фурье. В результате получаем:
, значит, для нахождения коэффициентов этого ряда можно использовать стандартные формулы Фурье. В результате получаем:
Получаем:


получилось разложение в ряд Фурье по синусам функции  , дополненной нечетным образом на промежуток
, дополненной нечетным образом на промежуток  и продолженной периодически с
и продолженной периодически с  на всю числовую ось, значит, для нахождения коэффициентов этого разложения можно использовать стандартные формулы Фурье; в результате получаем
на всю числовую ось, значит, для нахождения коэффициентов этого разложения можно использовать стандартные формулы Фурье; в результате получаем

Считаем записанный интеграл, а затем коэффициенты 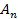 :
:






Запишем функцию 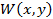 , используя формулу (13) и значения коэффициентов
, используя формулу (13) и значения коэффициентов 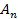 и
и  :
:

III.Складывая найденные функции V( x, y) и W( x, y), запишем искомую функцию 

Таким образом, используя модификацию метода Фурье получили решение краевой задачи (2) для уравнения Лапласа в прямоугольной двумерной области. Это решение имеет вид (15).
Дата добавления: 2020-04-25; просмотров: 88; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
